Omówienie zadania Pionek (I etap XXV OI)
Pierwszym krokiem rozwiązania jest zaczepienie wszystkich wektorów w punkcie \(O=(0,0)\). Poniższy rysunek przedstawia taką reprezentację przykładu z treści zadania z zaznaczonym przykładowym zestawem wektorów dających najdłuższą sumę.
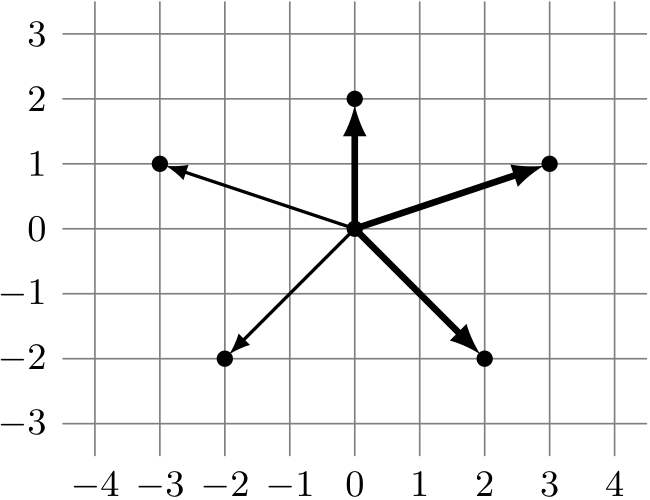
Zachodzi intuicyjny fakt, że rozwiązaniem zadania jest zbiór wszystkich wektorów zawartych w pewnej półpłaszczyźnie zaczepionej w punkcie \(O\). Dalej uzasadnimy ten fakt, a następnie pokażemy, jak rozwiązać zadanie za pomocą techniki tzw. zamiatania kątowego.
Najpierw jednak przypomnijmy pokrótce podstawowe własności iloczynu skalarnego i wektorowego dwóch wektorów – będą one przydatne tak w dowodzie, jak i w algorytmie. Więcej informacji o tych iloczynach można znaleźć w rozdziale poświęconym geometrii obliczeniowej w książce Wprowadzenie do algorytmów.
Iloczyn skalarny.
W tym opisie interesują nas tylko wektory dwuwymiarowe. Iloczyn skalarny wektorów \(\vec{v}_1=[x_1,y_1]\) i \(\vec{v}_2=[x_2,y_2]\) jest zdefiniowany jako \[\vec{v}_1 \cdot \vec{v}_2 = x_1x_2+y_1y_2.\] Własności iloczynu skalarnego:
- \(\vec{v}_1 \cdot \vec{v}_2=0\) wtedy i tylko wtedy, gdy \(\vec{v}_1\) i \(\vec{v}_2\) są prostopadłe;
- jeśli \(\vec{v}_1\) i \(\vec{v}_2\) są niezerowe, mają ten sam kierunek i zwrot, to \(\vec{v}_1 \cdot \vec{v}_2>0\), a jeśli mają ten sam kierunek i przeciwne zwroty, to \(\vec{v}_1 \cdot \vec{v}_2<0\);
- jeśli \(\vec{v}_1=a\cdot \vec{v}'_1\) dla pewnej stałej \(a\), to \(\vec{v}_1 \cdot \vec{v}_2=a\cdot (\vec{v}'_1 \cdot \vec{v}_2)\), a jeśli \(\vec{v}_1=\vec{u}_1+\vec{w}_1\), to \(\vec{v}_1 \cdot \vec{v}_2=\vec{u}_1 \cdot \vec{v}_2+\vec{w}_1 \cdot \vec{v}_2\);
- korzystając z powyższych własności można udowodnić, że jeśli \(\vec{v}_1\) jest wektorem jednostkowym, to \(\vec{v}_1 \cdot \vec{v}_2\) jest równe długości (ze znakiem) rzutu wektora \(\vec{v}_2\) na oś wyznaczoną przez wektor \(\vec{v}_1\) (tzn. wybieramy tylko składową wektora \(\vec{v}_2\) równoległą do \(\vec{v}_1\), a składową prostopadłą odrzucamy).
Dodajmy jeszcze, że dla dowolnego wektora \(\vec{v}\), \(\vec{v} \cdot \vec{v}\) jest równe kwadratowi jego długości.
Iloczyn wektorowy.
Iloczyn wektorowy wektorów \(\vec{v}_1=[x_1,y_1]\) i \(\vec{v}_2=[x_2,y_2]\) to \[\vec{v}_1 \times \vec{v}_2 = x_1y_2-x_2y_1.\] Formalnie iloczyn wektorowy jest zazwyczaj definiowany jako wektor, a podana wartość określa jego długość (ze znakiem); w tym opisie dla uproszczenia iloczyn wektorowy będziemy uważać po prostu za liczbę. Iloczyn wektorowy \(\vec{v}_1 \times \vec{v}_2\) jest:
- równy zero, gdy wektory \(\vec{v}_1\) i \(\vec{v}_2\) są współliniowe;
- dodatni, gdy wektor \(\vec{v}_2\) jest skierowany na lewo od wektora \(\vec{v}_1\);
- ujemny, gdy wektor \(\vec{v}_2\) jest skierowany na prawo od wektora \(\vec{v}_1\).
Dowód poprawności
Niech \(V\) będzie zbiorem wektorów oznaczających możliwe ruchy pionka, zaczepionych w punkcie \(O\). Interesuje nas podzbiór zbioru \(V\) dający wektor o najdłuższej sumie. Chcemy wykazać, że jako taki podzbiór możemy wybrać zbiór wszystkich wektorów zawartych w pewnej półpłaszczyźnie zaczepionej w punkcie \(O\).
Rozważmy zbiór wszystkich punktów, do których można dojść z punktu \(O\), używając każdego z wektorów ze zbioru \(V\) co najwyżej raz. Oznaczmy ten zbiór punktów przez \(A\), a przez \(B\) oznaczmy otoczkę wypukłą zbioru \(A\), czyli najmniejszy wielokąt wypukły zawierający zbiór \(A\). Wygląd obu zbiorów dla przykładu z treści zadania, z zaznaczonymi wszystkimi punktami optymalnymi oraz jedną z optymalnych ścieżek pionka, znajduje się na poniższym rysunku.
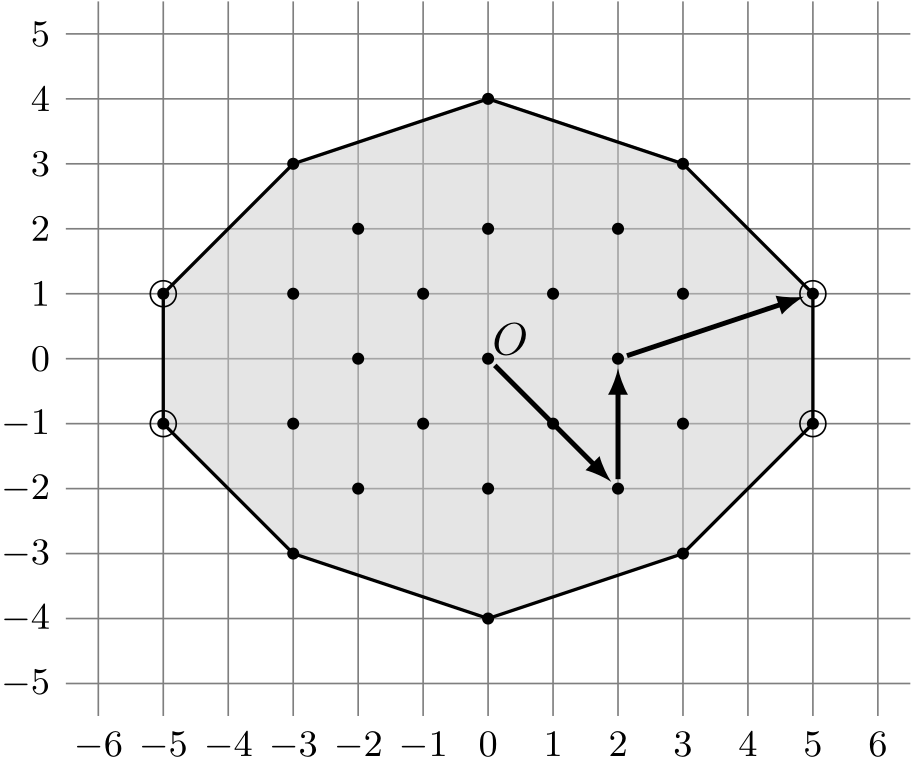
Interesuje nas ten z punktów ze zbioru \(A\), który leży najdalej od punktu \(O\). Okazuje się, że będzie to zawsze jeden z wierzchołków wielokąta \(B\). Wynika to z prostego spostrzeżenia, że jeśli \(P_1\) i \(P_2\) są dowolnymi punktami, to najdalszym od punktu \(O\) punktem trójkąta \(\Delta OP_1P_2\) jest jeden z wierzchołków \(P_1\), \(P_2\).
Niech \(P\) będzie wierzchołkiem wielokąta \(B\), który znajduje się najdalej od punktu \(O\). Ponieważ \(B\) jest wypukły, możemy narysować prostą \(p\), której jedynym punktem wspólnym z wielokątem \(B\) jest punkt \(P\). Niech \(\vec{v}\) będzie wektorem jednostkowym prostopadłym do prostej \(p\), skierowanym na zewnątrz wielokąta. Wówczas punkt \(P\) jest najdalszym punktem wielokąta \(B\) w kierunku wyznaczonym przez wektor \(\vec{v}\).
Wróćmy teraz do zbioru \(A\) i zastanówmy się, jak znaleźć najdalszy punkt tego zbioru położony w kierunku wyznaczonym przez dany wektor \(\vec{v}\). Przypomnijmy, że punkty ze zbioru \(A\) odpowiadają sumom pewnych podzbiorów wektorów ze zbioru \(V\). Jeśli chcemy, by suma podzbioru zbioru \(V\) dawała możliwie najdalszy punkt w kierunku wyznaczonym przez wektor \(\vec{v}\), powinniśmy do tego zbioru zaliczyć wszystkie wektory, których iloczyn skalarny z wektorem \(\vec{v}\) jest dodatni. Wektory mające zerowy iloczyn skalarny z wektorem \(\vec{v}\) możemy wziąć do sumy albo nie – jest to bez znaczenia. Wreszcie zbiór wektorów zaczepionych w punkcie \(O\), które dają nieujemny iloczyn skalarny z ustalonym wektorem \(\vec{v}\), to dokładnie zbiór wektorów zawartych w półpłaszczyźnie zaczepionej w punkcie \(O\), ograniczonej przez prostą prostopadłą do wektora \(\vec{v}\) i "skierowanej" w kierunku \(\vec{v}\).
Sortowanie kątowe
Aby znaleźć półpłaszczyznę, w której suma wektorów jest możliwie najdłuższa, zastosujemy zamiatanie kątowe. W tym celu musimy najpierw wszystkie wektory uporządkować wokół punktu \(O\), tzn. w kolejności, w jakiej napotykamy je, obiegając wokół wspólnego punktu zaczepienia. Jest to tzw. sortowanie kątowe (biegunowe).
Wśród wektorów do posortowania może znaleźć się wektor \([0,0]\). Nie jest jasne, w którym miejscu tego uporządkowania go umieścić. Najlepiej więc pozbyć się takich wektorów z rozważań, tym bardziej, że w przypadku naszego zadania nie odgrywają one żadnej roli. Jeśli po ich usunięciu nie pozostaną nam już żadne inne wektory, wynik jest jasny.
Do sortowania kątowego wybieramy dodatkowo wektor \(\vec{v}_0\) zaczepiony w punkcie \(O\) – zazwyczaj jest to wektor poziomy \([1,0]\). Następnie wszystkie wektory sortujemy niemalejąco względem kątów skierowanych, jakie tworzą z wektorem \(\vec{v}_0\). Zakładamy, że wektory leżące na lewo od wektora \(\vec{v}_0\) od mają dodatnie kąty, wektory leżące na prawo – ujemne kąty, wektory o tym samym kierunku i zwrocie co \(\vec{v}_0\) – kąt zerowy, a wektory o tym samym kierunku co \(\vec{v}_0\), ale przeciwnym zwrocie – kąt \(180^{\circ}\). Przykład takiego posortowania zbioru dziesięciu wektorów można znaleźć na poniższym rysunku.
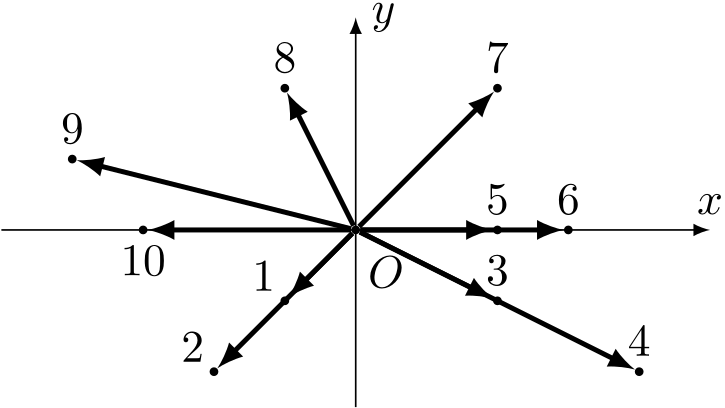
W ogólnym przypadku trzeba jeszcze zwrócić uwagę, w jakiej kolejności powinny występować wektory o tym samym kierunku i zwrocie. Zazwyczaj przyjmuje się, że takie wektory powinny być podane w kolejności niemalejących długości. W tym zadaniu nie jest to jednak istotne.
Opiszemy teraz dwa sposoby realizacji sortowania kątowego.
Pierwszy sposób.
Możemy obliczyć wartości kątów, jakie wektory tworzą z wektorem poziomym \(\vec{v}_0\), i sortować wektory względem tych kątów. Wartość kąta pomiędzy \(\vec{v}\) i \(\vec{v}_0\) możemy wyznaczyć za pomocą funkcji odwrotnych do funkcji trygonometrycznych. Świetnie nadaje się do tego celu funkcja atan2(y,x) z języka C++, implementująca rozszerzoną funkcję \(\mathrm{arctg}\). Funkcja ta, mając dane współrzędne wektora \([x,y]\), daje w wyniku liczbę rzeczywistą określającą wartość kąta skierowanego (w radianach) między tym wektorem a osią \(OX\). Wartość ta jest określona dokładnie tak, jak to opisaliśmy powyżej. Za pomocą tej funkcji możemy zatem bez problemu stworzyć funkcję porównującą do sortowania kątowego.
Trzeba pamiętać, że w przypadku obliczeń na wartościach kątów będących liczbami rzeczywistymi nieuchronnie pojawiają się błędy zaokrągleń. Ich konsekwencją mogłaby być na przykład niewłaściwa kolejność w posortowanym ciągu wektorów, które mają prawie taki sam kierunek. Nie wchodząc w szczegóły, gdy rozważamy punkty o całkowitych współrzędnych o wartościach bezwzględnych ograniczonych przez \(W\), problemy mogą pojawić się, gdy liczby rzędu \(\frac1{W^2}\) są na granicy dokładności używanego przez nas typu danych. W przypadku tak niewielkich współrzędnych jak w tym zadaniu wszystko będzie działać bez zarzutu, o ile użyjemy typu double lub long double.
Drugi sposób.
Możemy też obejść się bez funkcji trygonometrycznych (i ich odwrotności) i obliczeń na liczbach rzeczywistych. Nietrudno zaimplementować własną funkcję porównującą dwa wektory, tzn. zwracającą dla wektorów \(\vec{v}_1\) i \(\vec{v}_2\) prawdę wtedy i tylko wtedy, gdy \(\vec{v}_1\) powinien wystąpić w porządku kątowym przed \(\vec{v}_2\).
Skorzystamy z iloczynu wektorowego. Na podstawie znaków iloczynów wektorowych wektora \(\vec{v}_0\) z wszystkimi wektorami ze zbioru możemy pogrupować wszystkie wektory na takie które leżą na lewo od \(\vec{v}_0\), takie które leżą na prawo od \(\vec{v}_0\) i takie, które mają ten sam kierunek co \(\vec{v}_0\) (i zwrot ten sam albo przeciwny). Iloczyn wektorowy nie pozwala odróżnić wektorów o zwrocie zgodnym z \(\vec{v}_0\) od tych o zwrocie przeciwnym do \(\vec{v}_0\); do tego celu świetnie nadaje się jednak iloczyn skalarny, który ma dodatnią wartość dla wektorów o tym samym zwrocie co \(\vec{v}_0\) i ujemną dla tych o przeciwnym zwrocie.
Niestety wartość iloczynu wektorowego z wektorem \(\vec{v}_0\) nie odpowiada temu, w jakiej kolejności są ułożone wektory położone po tej samej stronie wektora \(\vec{v}_0\) (gdyż zależy ona także od ich długości). Natomiast jeśli już wiemy, że oba wektory \(\vec{v}_1\) i \(\vec{v}_2\) są położone na lewo (lub oba na prawo) od wektora \(\vec{v}_0\), to możemy stwierdzić, który z nich znajduje się wcześniej w porządku, sprawdzając, który z nich jest położony na lewo od drugiego. Możemy to stwierdzić, badając znak iloczynu \(\vec{v}_1 \times \vec{v}_2\). Zauważmy, że ta sama własność zachodzi także, jeśli do wektorów leżących na prawo od \(\vec{v}_0\) dorzucimy wektory o tym samym kierunku i zwrocie co \(\vec{v}_0\), a do wektorów leżących na lewo od \(\vec{v}_0\) wektory o tym samym kierunku co \(\vec{v}_0\), lecz przeciwnym zwrocie.
Pseudokod funkcji porównującej dwa wektory w porządku kątowym, zaimplementowanej za pomocą iloczynu wektorowego i skalarnego, można znaleźć poniżej.
function kierunek(\(\vec{v}\))
begin
if \(\vec{v}_0 \times \vec{v} < 0\) or (\(\vec{v}_0 \times \vec{v} = 0\) and \(\vec{v}_0 \cdot \vec{v} > 0\)) then
return -1; // prawo
else
return 1; // lewo
end
function komparator(\(\vec{v}_1\),\(\vec{v}_2\)) // czy \(\vec{v}_1\) jest wcześniej w porządku niż \(\vec{v}_2\)?
begin
\(a:=\mathrm{kierunek}(\vec{v}_1)\); \(b:=\mathrm{kierunek}(\vec{v}_2)\);
if \(a \ne b\) then
return \(a< b\);
else
return \(\vec{v}_1 \times \vec{v}_2> 0\);
end
Zastosowanie zamiatania kątowego
Zamiatanie kątowe jest wariantem techniki zamiatania, w którym miotła jest prostą zaczepioną w środku układu współrzędnych i obraca się w ustalonym kierunku, powiedzmy odwrotnie do ruchu wskazówek zegara. Obszar, który w danej chwili rozważamy w zamiataniu, to półpłaszczyzna domknięta położona po jednej, ustalonej stronie prostej zamiatającej; obszar ten nazwiemy obszarem zamiatania. Żeby wprowadzić tu jednoznaczność, możemy podzielić prostą zamiatającą na dwie półproste, lewą i prawą. Przyjmiemy, że obszarem zamiatania będzie półpłaszczyzna, którą odwiedzilibyśmy, poruszając się w lewo od prawej półprostej miotły aż do lewej półprostej miotły.
Naszym zadaniem jest znaleźć półpłaszczyznę zaczepioną w punkcie \(O\), taką że suma wszystkich wektorów leżących w tej półpłaszczyźnie jest jak najdłuższa. Wszystkich półpłaszczyzn jest oczywiście nieskończenie wiele, jednak – podobnie jak w zwykłym zamiataniu – możemy ograniczyć się do rozważenia tylko niektórych półpłaszczyzn. W tym zadaniu trzeba się jednak naprawdę dobrze zastanowić, jakie to powinny być półpłaszczyzny.
Rozważmy dowolną półpłaszczyznę zaczepioną w punkcie \(O\). Załóżmy najpierw, że prosta ją wyznaczająca zawiera jeden z wejściowych wektorów. Jest \(2n\) takich półpłaszczyzn: \(n\) takich, których prawa półprosta zawiera któryś z wektorów, i \(n\) takich, których lewa półprosta zawiera któryś z wektorów.
Załóżmy teraz, że żaden z wektorów nie leży na prostej wyznaczającej półpłaszczyznę. Oznaczmy taką półpłaszczyznę przez \(G\). Wówczas półpłaszczyznę \(G\) możemy zacząć obracać do momentu, gdy wyznaczająca ją prosta zatrzyma się na jednym z wektorów. Zauważmy, że może to nastąpić w przypadku lewej półprostej, prawej półprostej lub obu półprostych naraz. Przyjmijmy, że obracaliśmy półpłaszczyznę w kierunku zgodnym z ruchem wskazówek zegara, czyli przeciwnie do kierunku zamiatania. Przez cały czas obracania półpłaszczyzny zbiór wektorów w niej zawartych był dokładnie taki sam. Dopiero w momencie, gdy prosta wyznaczająca półpłaszczyznę pokryła któryś z wektorów, zbiór ten mógł ulec zmianie. Oznaczmy otrzymaną w wyniku tego obrotu półpłaszczyznę przez \(H\). Jeśli tylko lewa półprosta \(H\) zawiera jakiś wektor, to zbiór wektorów zawartych w \(H\) jest taki sam, jak zbiór wektorów zawartych w \(G\). Zauważmy, że wtedy nie musieliśmy w ogóle rozpatrywać półpłaszczyzny \(G\), ponieważ z punktu widzenia zadania jest ona równoważna półpłaszczyźnie \(H\), którą rozważyliśmy jako jedną z \(2n\) półpłaszczyzn wyznaczonych przez wektor. Jeśli natomiast to prawa półprosta \(H\) zawiera jakiś wektor lub obie półproste zawierają wektory, zbiór wektorów reprezentowany przez \(H\) jest inny niż ten reprezentowany przez \(G\). To oznacza, że półpłaszczyzny \(G\) i \(H\) nie są równoważne, więc musimy rozważyć je obie. Przykłady, że rzeczywiście może to być potrzebne, można obejrzeć na poniższych rysunkach: na obu z nich zaznaczona półpłaszczyzna daje największy możliwy wynik i nie jest równoważna z żadną półpłaszczyzną opartą na którymś z wektorów.
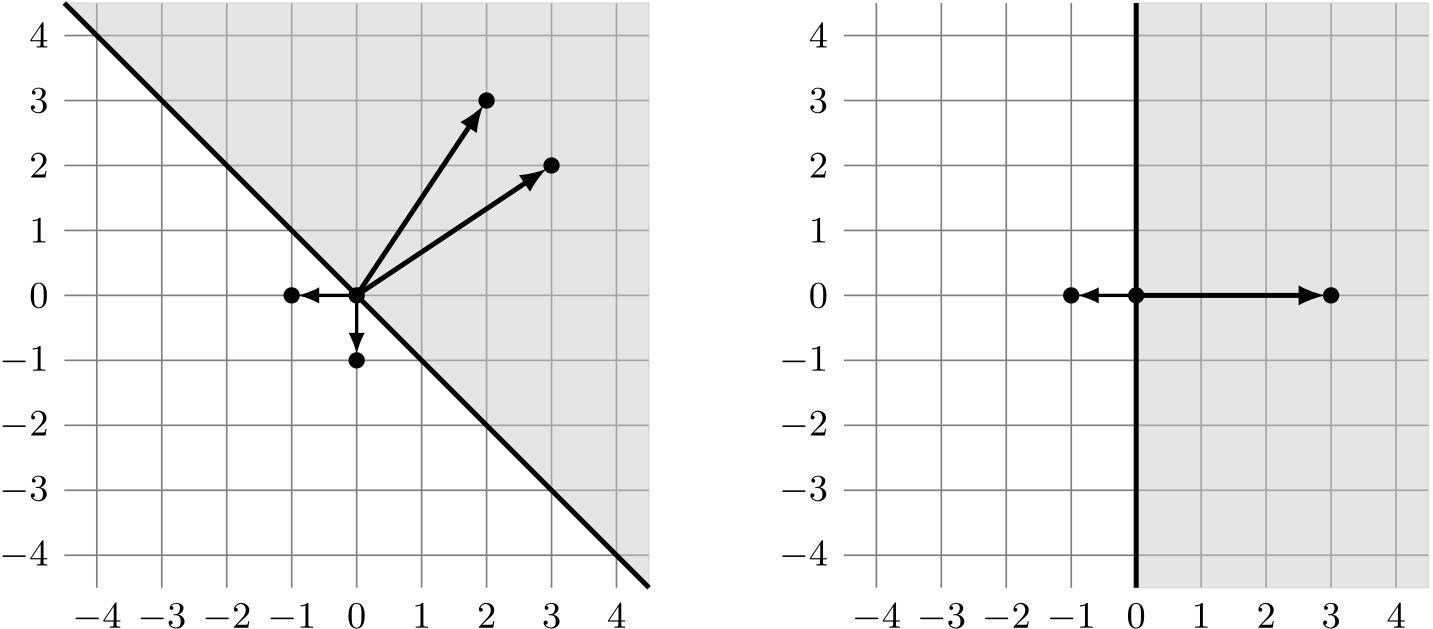
W tym przypadku półpłaszczyznę \(G\) możemy jednak zastąpić półpłaszczyzną prawie taką samą jak półpłaszczyzna \(H\), tylko niezawierającą wektorów położonych na prawej półprostej. Możemy wyobrazić sobie, że półpłaszczyznę \(H\) obracamy minimalnie przeciwnie do kierunku ruchu wskazówek zegara – tylko o tyle, żeby nie zawierała tych wektorów na prawej półprostej, ale nie o tyle, by którakolwiek z półprostych dotknęła któregokolwiek z pozostałych wektorów.
Ostatecznie chcemy rozważyć następujące typy półpłaszczyzn:
- zawierające któryś z wektorów na lewej półprostej;
- zawierające któryś z wektorów na prawej półprostej;
- minimalnie przesunięte w stosunku do półpłaszczyzny zawierającej któryś z wektorów na prawej półprostej.
Zdarzeniami w zamiataniu będą te momenty, kiedy prawa półprosta zawiera któryś z wektorów. W trakcie zamiatania będziemy pamiętać sumę wektorów znajdujących się w obszarze zamiatania.
Przed rozpoczęciem zamiatania warto dokonać jeszcze jednej drobnej modyfikacji danych wejściowych. Otóż zauważmy, że jeśli mamy grupę wektorów "remisujących" w porządku kątowym, czyli mających ten sam kierunek i zwrot, to wszystkie one są równoważne z punktu widzenia rozwiązania: albo wszystkie są zawarte w półpłaszczyźnie, albo żaden z nich nie jest. Możemy więc za każdym razem zastąpić wszystkie te wektory jednym, będącym ich sumą, i w ten sposób pozbyć się remisów. Aby znaleźć grupy takich wektorów, wystarczy sprawdzać dla każdych dwóch kolejnych wektorów na posortowanej liście, czy ich iloczyn wektorowy jest równy 0, a skalarny dodatni.
Pojedyncze zamiatanie zrealizujemy tak, że będziemy iterować dwoma indeksami po posortowanej kątowo liście wszystkich wektorów, którą będziemy traktować jako listę cykliczną. Indeksy te nazwiemy głównym i pomocniczym i będą one intuicyjnie odpowiadały ruchom odpowiednio prawej i lewej półprostej (tak, jakby poruszały się one niezależnie). Ustawmy oba indeksy na pierwszym elemencie listy. Następnie zacznijmy przesuwać indeks pomocniczy. Będziemy to czynić tak długo, dopóki wskazywane przez niego wektory będą należeć do półpłaszczyzny położonej na lewo od bieżącego ułożenia prawej półprostej. Załóżmy, że indeks główny wskazuje w danym momencie wektor \(\vec{v}\). Wówczas indeks pomocniczy przesuwamy tak długo, dopóki wskazywany przez niego wektor \(\vec{v}'\) znajduje się po lewej stronie wektora \(\vec{v}\) lub ma współliniowy kierunek, lecz przeciwny zwrot. Zatrzymujemy się tuż za ostatnim wektorem o takiej własności.
Suma wszystkich wektorów od indeksu głównego do ostatniego wektora przed indeksem pomocniczym będzie odpowiadała półpłaszczyźnie spełniającej warunek 2. Żeby rozpatrzyć przypadek 3, musimy odjąć od sumy wektor \(\vec{v}\).
Następnie przesuwamy indeks główny o jedną pozycję. Zauważmy, że teraz możemy rozpocząć przesuwanie indeksu pomocniczego od pozycji, na której zakończył się przesuwać poprzednio. W ten sposób ruch obu indeksów działa na zasadzie gąsienicy i zamiatanie ma złożoność czasową \(O(n)\).
Przykładową implementację przedstawia poniższy pseudokod. Zakładamy w nim, że tablica \(V[0..n-1]\) zawiera posortowaną kątowo listę wszystkich wektorów, którą przechodzimy cyklicznie. Po liście wektorów iterujemy się za pomocą indeksów \(\mathit{główny}\) i \(\mathit{pomoc}\), przy czym dla ułatwienia implementacji indeks \(\mathit{pomoc}\) wskazuje na pierwszy wektor tuż za tymi, które są w aktualnie rozważanej półpłaszczyźnie. Innymi słowy, indeksy tworzą przedział domknięto-otwarty. W szczególności zaczynamy od sytuacji, w której oba indeksy wskazują na początek listy wektorów – co oznacza przedział pusty, który następnie rozszerzamy. Przedział pusty może wystąpić na początku kroku także wtedy, gdy w poprzednim kroku półpłaszczyzna oparta prawą półprostą o wektor \(V[\mathit{główny}]\) zawierała tylko ten wektor.
W pseudokodzie jest jeden przypadek brzegowy: jeśli stwierdzimy, że wszystkie wektory leżą w aktualnie rozważanej półpłaszczyźnie, to musimy przerwać iterowanie indeksem \(\mathit{pomoc}\), gdyż inaczej doszłoby do zapętlenia. Wtedy na sam koniec obsługi tego kroku nasze indeksy na chwilę się zrównują, co jednak w tym przypadku oznacza przedział wszystkich wektorów, a nie przedział pusty. Nasz sposób obsługi tego przypadku jest poprawny, jeśli \(n> 1\).
Poprawne napisanie tego typu funkcji wymaga pewnej ostrożności. Przykładowo pozostawiamy jako pouczające ćwiczenie stwierdzenie, dlaczego poniższy pseudokod nie jest poprawny, jeśli na liście może być więcej niż jeden wektor o tym samym kierunku i zwrocie.
function zamiatanie(\(V\),\(n\))
begin
\(\mathit{wynik}:=0\);
\(\mathit{pomoc}:=0\);
\(\mathit{suma}:=[0,0]\);
for \(\mathit{główny}:=0\) to \(n-1\) do begin
// niezmiennik: \(\mathit{suma}\) to suma wektorów w przedziale "domknięto-otwartym"
while \(V[\mathit{główny}] \times V[\mathit{pomoc}] \ge 0\) do begin
\(\mathit{suma}:=\mathit{suma}+V[\mathit{pomoc}]\);
\(\mathit{pomoc}:=(\mathit{pomoc}+1) \bmod n\);
// przypadek szczególny: wszystkie wektory są w półpłaszczyźnie
if \(\mathit{pomoc}=\mathit{główny}\) then break;
end
// przypadek 2
\(\mathit{wynik}:=\max(\mathit{wynik},\mathit{suma} \cdot \mathit{suma})\);
\(\mathit{suma}:=\mathit{suma}-V[\mathit{główny}]\);
// przypadek 3
\(\mathit{wynik}:=\max(\mathit{wynik},\mathit{suma} \cdot \mathit{suma})\);
end
return \(\mathit{wynik}\);
end
Podsumujmy wszystkie kroki rozwiązania wzorcowego:
- Usuwamy wszystkie wektory zerowe. Jeśli nie pozostał żaden inny wektor, wynikiem jest 0.
- Sortujemy wektory kątowo.
- Każdą grupę wektorów remisujących w porządku kątowym zastępujemy ich sumą. Jeśli pozostał tylko jeden wektor, wynikiem jest kwadrat jego długości.
- Uruchamiamy funkcję zamiatanie.
- Odbijamy wszystkie wektory względem osi \(OX\).
- Sortujemy wektory kątowo.
- Uruchamiamy funkcję zamiatanie i wypisujemy maksimum z wyników podanych przez oba wywołania tej funkcji.
W rozwiązaniu należało także pamiętać, by funkcje obliczające iloczyny skalarne i wektorowe operowały na zmiennych całkowitych 64-bitowych. Jest to konieczne, jako że w kroku 3 powyższego rozwiązania możemy utworzyć wektory istotnie dłuższe niż te dane na początku.
Opis zadania powstał na podstawie opracowania w książce Przygody Bajtazara.











