Omówienie zadania Dwa długie lizaki (III etap XXV OI)

Treść zadania

W zadaniu mamy dane dwa lizaki. Każdy lizak można opisać za pomocą ciągu binarnego, w którym bit 0 oznacza – powiedzmy – segment truskawkowy, a bit 1 – segment waniliowy. Lizaki są podane w skompresowanej postaci, w której każdy maksymalny fragment stały, zwany segmentem lizaka, jest reprezentowany przez wspólny bit oraz długość segmentu. Przez \(n_{\max}\) i \(m_{\max}\) oznaczamy, odpowiednio, maksymalną długość lizaka i maksymalną liczbę segmentów w lizaku. Dla uproszczenia w opisie parametry \(n_{\max}\) i \(m_{\max}\) oznaczamy przez \(n\) i \(m\). W zadaniu mamy \(m \le 1000\), \(n \le 10^9\). Oznaczmy kolejne segmenty pierwszego lizaka przez \(A_1 \ldots A_{m_1}\), a drugiego przez \(B_1 \ldots B_{m_2}\).

Wektorem lizaka nazwiemy parę \((x,y)\), w której \(x\) oznacza łączną liczbę zer, a \(y\) łączną liczbę jedynek w lizaku. Wektor lizaka \(L\) oznaczymy jako \(W(L)\). Naszym zadaniem jest wybrać możliwie najdłuższy fragment pierwszego lizaka i fragment drugiego lizaka tak, aby te fragmenty miały ten sam wektor.

Rozwiązanie \(O(n^2 \log n)\) lub \(O(n^2)\)

Najprostsze rozwiązanie w ogóle nie korzysta z tego, że lizaki są podane w postaci skompresowanej. Generujemy wektory wszystkich fragmentów pierwszego i drugiego lizaka. Następnie sprawdzamy, które wektory można wygenerować z obu lizaków. Możemy to zrobić, posortowawszy wektory w czasie \(O(n^2 \log n)\). Możemy też użyć tablicy haszującej, co da oczekiwany czas \(O(n^2)\). Tego typu rozwiązania przechodziły pierwsze dwa podzadania.

Rozwiązanie \(O(m^4)\)

Dla każdej czwórki indeksów \(i,j,i',j'\) takich że \(1 \le i \le j \le m_1\) i \(1 \le i' \le j' \le m_2\) chcemy sprawdzić, czy z fragmentów \(X=A_i \cdots A_j\) i \(Y=B_{i'} \cdots B_{j'}\) możemy wyłamać lizaki o takich samych wektorach, ucinając jedynie pewne fragmenty segmentów \(A_i\), \(A_j\), \(B_{i'}\), \(B_{j'}\). Jeśli jest to możliwe, chcemy wyznaczyć maksymalną długość takich lizaków.

W tym celu przydatne okazuje się podejście geometryczne. Z fragmentu \(X\) stworzymy prostokąt \(P(X)\) na płaszczyźnie następująco: jeśli \(i < j\), to prostokąt ma lewy dolny róg w punkcie \(W(A_{i+1} \cdots A_{j-1})\) (czyli takim jak wektor lizaka \(A_{i+1} \cdots A_{j-1}\)), a prawy górny w punkcie \(W(A_i \cdots A_j)\). Jeśli natomiast \(i=j\), to prostokąt jest zdegenerowany – jest to odcinek łączący punkt \((0,0)\) z punktem \(W(A_i)\). W ten sposób zbiór wektorów lizaków, jakie możemy wyłamać z fragmentu \(X\), ucinając jedynie pewne fragmenty segmentów \(A_i\) i \(A_j\), tworzy właśnie prostokąt \(P(X)\). Analogicznie tworzymy prostokąt \(P(Y)\) opisujący fragment \(Y\). Teraz naszym zadaniem jest stwierdzić, czy prostokąty \(P(X)\) i \(P(Y)\) mają punkt wspólny, a jeśli tak, wyznaczyć punkt wspólny o maksymalnej sumie współrzędnych. Nazwiemy ten punkt maksymalnym punktem wspólnym tych dwóch prostokątów. Jeśli \(P(X)=[x_1,x_2] \times [y_1,y_2]\) i \(P(Y) = [x'_1,x'_2] \times [y'_1,y'_2]\), to szukany prostokąt ma rzut \(I:=[x_1,x_2] \cap [x'_1,x'_2]\) na oś X i rzut \(J:=[y_1,y_2] \cap [y'_1,y'_2]\) na oś Y. Maksymalnym punktem wspólnym jest punkt \((\max I,\max J)\), o ile oba te przedziały są niepuste.

Jeśli na początku obliczymy wektory kolejnych prefiksów \(A_1 \cdots A_j\) i \(B_1 \cdots B_{j'}\), to wektory fragmentów \(X\) i \(Y\) możemy wyznaczyć w czasie stałym jako różnice odpowiednich wektorów prefiksowych. Następnie każdą czwórkę indeksów \(i,j,i',j'\) rozpatrujemy w czasie stałym za pomocą powyższych wzorów, co daje łącznie czas \(O(m^4)\). Tego typu rozwiązanie mogło przejść trzecie i czwarte podzadanie.

Rozwiązanie \(O(m^3 \log m)\)

Poprzednie rozwiązanie można przyspieszyć do złożoności \(O(m^3 \log m)\), choć jest to niestety dość techniczne. Dla każdych indeksów \(i,j,i'\) chcemy wyznaczyć długość najdłuższych lizaków o takich samych wektorach, przy czym pierwszy lizak ma zawierać segmenty \(A_i \ldots A_j\) i może zawierać fragmenty segmentów \(A_{i-1}\) oraz \(A_{j+1}\), a drugi lizak ma zaczynać się fragmentem segmentu \(B_{i'-1}\) i dalej segmentem \(B_{i'}\). Ustalamy \(i\) oraz \(i'\), a następnie wyniki dla rosnących \(j\) wyznaczamy metodą gąsienicy.

Idea jest taka, że dla danego indeksu \(j\) wyznaczamy najmniejszy taki indeks \(j'\), że wektor lizaka \(B_{i'-1} \cdots B_{j'}\) dominuje wektor lizaka \(A_i \ldots A_j\) na obu współrzędnych, po czym wykonujemy operacje zmierzające do zrównoważenia wektorów, a następnie od uzyskania największej możliwej sumy współrzędnych. Indeksy \(j'\) będą tylko wzrastać. Niestety, podczas równoważenia możemy musieć skorzystać z segmentów dużo dalszych niż ten pod indeksem \(j'\) i trzeba to zrobić w czasie jedynie \(O(\log m)\). Implementacja rozwiązania wychodzi dosyć złożona, więc szczegóły pomijamy. Jeśli któryś z zawodników napisał tego typu rozwiązanie, mógł zaliczyć podzadania piąte i szóste.

Pierwsze rozwiązanie wzorcowe \(O(m^2 \log m)\)

Odpowiednie wykorzystanie podejścia geometrycznego prowadzi do rozwiązania o złożoności \(O(m^2 \log m)\). Podamy dwa rozwiązania o takiej złożoności różniące się liczbą poczynionych obserwacji.

Przypomnijmy, że dla każdej pary indeksów \(1 \le i \le j \le m_1\), zbiór wektorów lizaków, jakie możemy wyłamać z fragmentu \(X=A_i \cdots A_j\), ucinając jedynie pewne fragmenty segmentów \(A_i\) i \(A_j\), tworzy prostokąt \(P(X)\); podobnie w przypadku lizaka \(B\). W ten sposób z każdego z lizaków otrzymujemy kolekcję zawierającą \(O(m^2)\) prostokątów; oznaczmy te kolekcje przez \(R_1\) i \(R_2\). Podobnie jak poprzednio, chcemy znaleźć maksymalny punkt wspólny jakiegoś prostokąta z \(R_1\) i jakiegoś prostokąta z \(R_2\). Problem ten można rozwiązać za pomocą metody zamiatania.

Na podstawie wzorów z rozwiązania \(O(m^4)\) można zauważyć, że maksymalny punkt wspólny dwóch prostokątów będzie jednym z poniższych:

1. prawym górnym wierzchołkiem jednego z prostokątów z \(R_1\) zawartym w jakimś prostokącie z \(R_2\)
2. prawym górnym wierzchołkiem jednego z prostokątów z \(R_2\) zawartym w jakimś prostokącie z \(R_1\)
3. punktem przecięcia poziomego boku prostokąta z \(R_1\) z pionowym bokiem prostokąta z \(R_2\)
4. punktem przecięcia poziomego boku prostokąta z \(R_2\) z pionowym bokiem prostokąta z \(R_1\).

Pierwsze dwa przypadki są symetryczne; podobnie kolejne dwa. Mamy zatem do rozwiązania dwa osobne problemy. Dla uproszczenia przyjmujemy, że kolekcje \(R_1\) i \(R_2\) zawierają tyle samo prostokątów.

Problem 1: Dane jest \(k\) prostokątów i \(k\) punktów na płaszczyźnie. Dla każdego punktu chcemy stwierdzić, czy należy do któregoś z prostokątów, a następnie wybrać ten z punktów spełniających ten warunek, który ma maksymalną sumę współrzędnych. Aby rozwiązać Problem 1, zamiatamy płaszczyznę pionową miotłą np. od lewej do prawej. Zdarzeniami w zamiataniu są pionowe boki prostokątów i punkty. Prostokąty, które aktualnie przecinają miotłę, trzymamy na drzewie przedziałowym typu "wstaw przedział, pytaj o punkt". Gdy w zamiataniu napotkamy pionowy bok prostokąta, dodajemy lub usuwamy przedział rzędnych mu odpowiadających w zależności od tego, czy pionowy bok był lewym czy prawym bokiem prostokąta. Gdy napotykamy punkt, pytamy, czy jest on zawarty w jakimś przedziale przechowywanym w drzewie przedziałowym.

W przypadku wielu różnych zdarzeń o tej samej odciętej, najpierw rozpatrujemy lewe boki prostokątów, następnie punkty, a na końcu prawe boki. Żeby współrzędne punktów i prostokątów były rzędu \(O(k)\), co pozwoli je wygodnie wstawiać do drzewa przedziałowego, przenumerowujemy je na początku.

Problem 2: Dane jest \(k\) odcinków poziomych i \(k\) pionowych. Dla każdego odcinka pionowego chcemy wyznaczyć punkt, w którym przecina się z jakimś odcinkiem poziomym, a jeśli takich punktów jest więcej, to punkt o maksymalnej sumie współrzędnych. Tym razem miotła jest drzewem przedziałowym typu "wstaw punkt, spytaj o przedział". W drzewie przedziałowym trzymamy rzędne odcinków poziomych przecinanych przez miotłę. Gdy w zamiataniu napotykamy odcinek pionowy, pytamy, czy w przedziale jego rzędnych jest jakiś punkt przechowywany w drzewie przedziałowym, a jeśli tak, podajemy punkt o maksymalnej współrzędnej.

W ten sposób każdy z problemów rozwiązujemy w czasie \(O(k \log k)\), ze względu na złożoność operacji na drzewie przedziałowym. Dla \(k=O(m^2)\) otrzymujemy rozwiązanie zadania w czasie \(O(m^2 \log m)\). Rozwiązania o tej złożoności powinny przechodzić wszystkie podzadania.

Drugie rozwiązanie wzorcowe \(O(m^2 \log m)\)

Wyeliminujemy z rozwiązania Problem 1. W tym celu poczynimy następującą obserwację.

Obserwacja. Istnieje optymalne rozwiązanie, w którym:

1. albo jeden z lizaków bierzemy w całości,
2. albo oba lizaki wynikowe zaczynają się lub kończą na krawędzi segmentu.

Dowód. Weźmy dowolne rozwiązanie optymalne. Niech \(S_1\) będzie zbiorem bitów, które bezpośrednio sąsiadują z pierwszym lizakiem po lewej i prawej stronie. Analogicznie definiujemy \(S_2\) dla drugiego lizaka. Przecięcie zbiorów \(S_1\) i \(S_2\) musi być puste, bo inaczej moglibyśmy rozszerzyć lizaki o bit ze zbioru \(S_1 \cap S_2\). Przykładowo, dla poniższych fragmentów lizaków (kolor biały oznacza bit 0, a kolor szary – bit 1) o wektorze \((8,7)\) przecięcie \(S_1 \cap S_2\) nie byłoby puste i faktycznie fragmenty można by wydłużyć w prawo:

Jeśli przecięcie jest puste, gdyż \(S_1\) lub \(S_2\) jest zbiorem pustym, to znaczy, że jeden z lizaków bierzemy w całości. To odpowiada pierwszemu przypadkowi z obserwacji.

Załóżmy teraz bez straty ogólności, że \(S_1 = \{0\}\) i \(S_2 = \{1\}\). Jeśli pierwszy lizak nie zaczyna się i nie kończy na granicy segmentu, to znaczy, że możemy go przesunąć o jedną pozycję np. w prawo. Nie możemy przesuwać w nieskończoność i w pewnym momencie trafimy na granicę segmentu. Analogicznie przesuwamy drugi lizak. Przykładowo, poniżej znajduje się optymalne rozwiązanie poprzedniego przykładu; fragment drugiego lizaka można dosunąć w prawo tak, by kończył się na granicy segmentu:

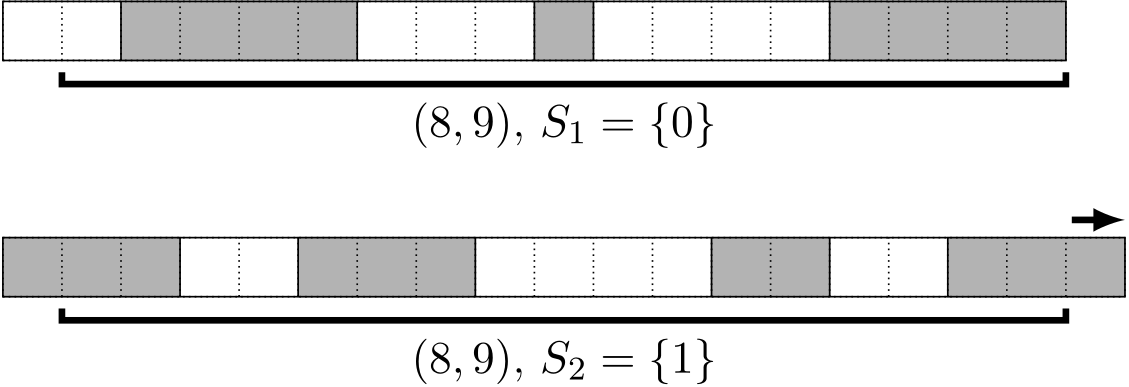
To kończy dowód obserwacji.

Obserwacja 1 uprasza algorytm rozwiązujący zadanie. Jeśli zachodzi pierwszy przypadek z obserwacji, to krótszy z lizaków bierzemy w całości. Musimy znaleźć fragment dłuższego lizaka, który ma taki sam wektor jak krótszy lizak. W tym celu wystarczy wyznaczyć wektor \(w\) krótszego lizaka, a następnie sprawdzić, czy należy on do któregoś z \(O(m^2)\) prostokątów generowanych przez dłuższy lizak. Daje to algorytm w czasie \(O(m^2)\). Ten podproblem można także rozwiązać za pomocą algorytmu gąsienicy w czasie \(O(m)\), ale w tym zadaniu nie zachodzi taka potrzeba.

Załóżmy teraz, że zachodzi drugi przypadek z obserwacji. Tym razem dla każdej pary indeksów \(1 \le i \le j \le m_1\), wyznaczamy zbiór wektorów lizaków, jakie możemy wyłamać z fragmentu \(X=A_i \cdots A_j\), ucinając pewien fragment segmentu \(A_i\) lub pewien fragment segmentu \(A_j\), ale nie oba naraz. Ten zbiór wektorów to suma dwóch odcinków, z których każdy jest albo pionowy, albo poziomy. Mamy zatem dwie kolekcje odcinków pionowych i poziomych, \(R_1\) i \(R_2\), i chcemy wyznaczyć maksymalny punkt przecięcia odcinka z \(R_1\) z odcinkiem z \(R_2\).

Na podstawie dowodu obserwacji wiemy, że jeśli w rozwiązaniu optymalnym jeden z końców fragmentu pierwszego lizaka jest położony ściśle wewnątrz segmentu i jeden z końców fragmentu drugiego lizaka jest położony ściśle wewnątrz segmentu, to te segmenty mają różne bity. W języku odcinków oznacza to, że wystarczy szukać przecięć odcinków pionowych z \(R_1\) z odcinkami poziomymi z \(R_2\) i odwrotnie. W ten sposób otrzymujemy dokładnie instancje Problemu 2 opisanego powyżej, które rozwiązujemy w czasie \(O(m^2 \log m)\).