Omówienie zadania Kompresja drzew binarnych (eliminacje do IOI 2020, dzień 2)

Obliczmy na początku ciąg \(m_1,\ldots,m_k\) taki że \(m_i\) to liczba liści na głębokości \(i\).

Rozwiązanie zachłanne nie działa

Mogłoby się wydawać, że zawsze opłaca się posortować liście niemalejąco po wysokościach i w ten sposób dzielić na poddrzewa. To jednak nie działa np. dla ciągu \(m_i=[0, 0, 2, 2, 8, 16, 0, 32]\). Czarne wierzchołki na rysunku poniżej przedstawiają drzewo po kompresji.

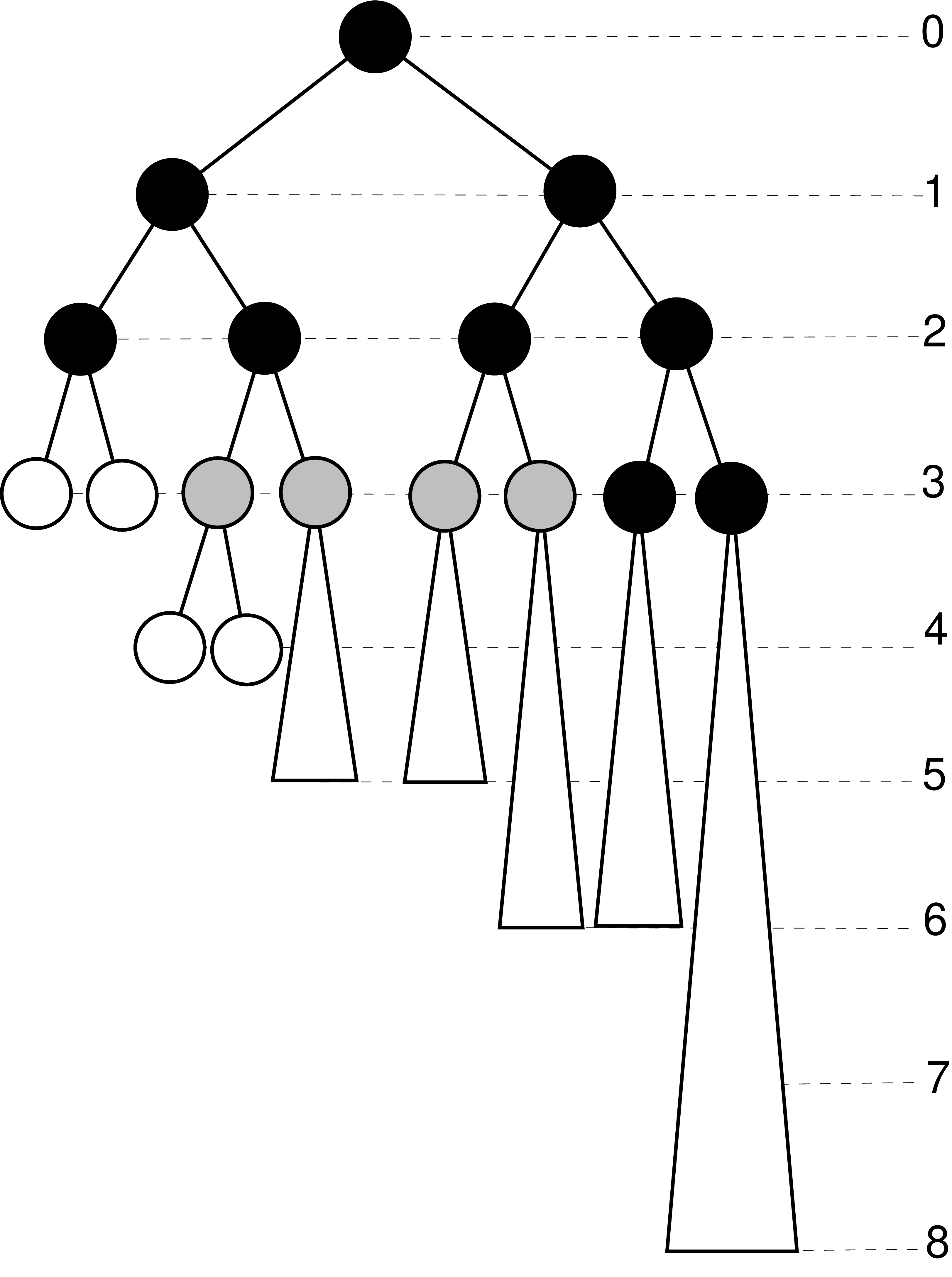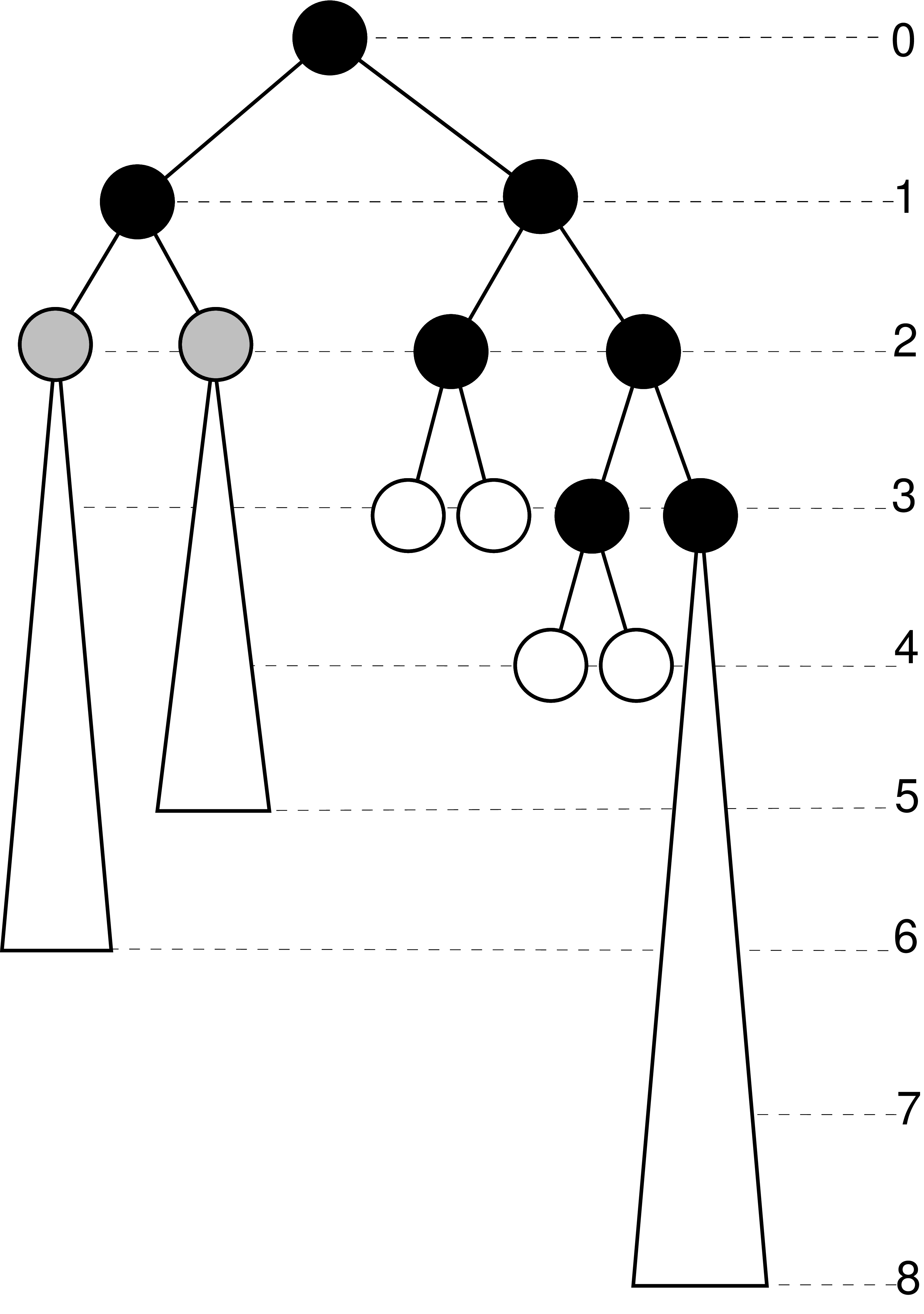Rozmaite rozwiązania zachłanne okazują się niepoprawne. Np. wzięcie dla każdej pary kolejnych poziomów zawsze największej potęgi dwójki nie mniejszej niż \(2(m_{i-1}-x)+y\), idąc od 1 do \(k\) albo idąc od \(k\) do 1.

Podzadania 1 i 2

Rozwiązanie to działa w czasie \(O(n^2)\) i opiera się na programowaniu dynamicznym. Warto zacząć od kilku spostrzeżeń:

1. Ciąg \(l_i\) jest poprawny wtedy i tylko wtedy gdy spełnia \(\sum_{i=1}^n 2^{-l_i} = 1\).
2. Nie każda permutacja ciągu \(l_i\) daje możliwy ciąg głębokości liści od lewej do prawej. Np. 1, 2, 2 jest poprawne, ale 2, 1, 2 nie.
3. Aby stworzyć dowolne poprawne drzewo z ciągu \(l_i\), wystarczy w każdym kroku łączyć dwa najgłębsze liście, zamieniając dwa liście o głębokości \(x\) na jeden liść o głębokości \(x-1\). Alternatywna metoda to po prostu posortować ciąg \(l_i\) niemalejąco.

Podproblemem nazwiemy dowolny ciąg \(m'_1,\ldots,m'_p\), taki że \(p \le k\), \(m'_1=m_1\), \ldots, \(m'_{p-1}=m_{p-1}\) oraz \(m'_p \le m_p\). Poddrzewo nazwiemy półpełnym, jeśli liście w tym poddrzewie są położone na co najwyżej dwóch różnych głębokościach. W programowaniu dynamicznym będziemy obliczać dla każdego podproblemu \(m'_1,\ldots,m'_p\) wartość \(DP[p,m'_p]\) oznaczającą minimalną liczbę półpełnych poddrzew, z korzeniami umieszczonymi na dowolnych głębokościach, mających łącznie \(m'_i\) liści na głębokości \(i\) dla każdego \(i\). Uwaga: nie wymagamy, aby te poddrzewa dały się połączyć w jedno drzewo. Ten warunek zostanie wymuszony w stanie \(DP[k,m_k]\).

Przykładowo, poniższe rysunki przedstawiają wyniki dla podproblemów \(\langle 0, 0,3,3\rangle\) (dwa poddrzewa), \(\langle 0, 0,3,4\rangle\) (dwa poddrzewa) i \(\langle 0, 0,3,5\rangle\) (trzy poddrzewa). Korzenie poddrzew oznaczono kwadracikami.

Programowanie dynamiczne wygląda wtedy następująco.

DP[0,0] := 0;
DP[i,y] := infty for 0 <= i <= k, 0 <= y <= m_i;
for i := 1 to k do
    for y := 0 to m_i do
        DP[i,y] := min_{0 <= x <= m_{i-1}} DP[i-1,x] + __builtin_popcount(2(m_{i-1}-x)+y));
return 2 * DP[k,m_k] - 1;

Warto jeszcze wytłumaczyć, skąd w pseudokodzie wzięła się zliczająca zapalone bity funkcja __builtin_popcount. Otóż przejście ze stanu \(DP[i-1,x]\) do stanu \(DP[i,y]\) wymaga połączenia \(m_{i-1}-x\) liści na głębokości \(i-1\) z \(y\) liśćmi na głębokości \(i\). Jak łatwo zauważyć, w półpełnym drzewie mającym \(a\) liści na mniejszej głębokości i \(b\) na większej, liczba \(2a+b\) jest potęgą dwójki. W ten oto sposób wynik zależy od rozkładu liczby \(2(m_{i-1}-x)+y\) na najmniejszą liczbę potęg dwójki.

Rozwiązanie działa w czasie \(O(kM^2) = O(n^2)\), przy czym \(M = \max m_i\), o ile wartości funkcji __builtin_popcount mamy stablicowane dla wszystkich interesujących nas argumentów.

Odtwarzanie wyniku odbywa się za pomocą standardowego wyznaczania ojców stanów w programowaniu dynamicznym, przy czym konstrukcja ostatecznego drzewa korzysta ze spostrzeżeń przedstawionych na wstępie.

Rozwiązanie wzorcowe

Rozwiązanie wzorcowe działa w czasie \(O(n \log n)\). Korzystamy w nim z faktu, że zamiast rozważać kroki dynamiczne złożone z wielu drzew, można zawsze rozważać jedno. Nie otrzymamy nigdy zysku ze stworzenia dwóch różnych poddrzew, w których każde ma liście na tych samych dwóch kolejnych głębokościach – możemy zamienić liście miejscami tak, aby tylko jedno z nich miało dwie głębokości. Wobec tego aby policzyć stan \(DP[i][y]\) wystarczą wartości \(DP[i][y-2^z]\) oraz \(DP[i-1][m_{i-1} - \frac{2^z - y}{2}]\).