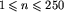 ,
, 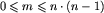 .
.W związku z ostatnimi wpadkami swoich agentów, Urząd Ochrony Bajtocji postanowił usprawnić działalność.
Największym dotychczasowym problemem było bezpieczne urządzanie spotkań agentów. Twój program ma pomóc w rozwiązaniu tego problemu. Dla podanego opisu sieci dróg Bajtocji oraz początkowej pozycji dwóch agentów, powinien stwierdzać, czy możliwe jest bezpieczne spotkanie tych agentów.
Żeby spotkanie uznać za bezpieczne agenci muszą przestrzegać następujących reguł:
Napisz program, który:
W pierwszym wierszu pliku tekstowego AGE.IN znajdują się dwie liczby całkowite n i m, oddzielone pojedynczym odstępem, gdzie 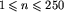 ,
, 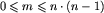 .
.
W drugim wierszu znajdują się dwie liczby całkowite a1 i a2 oddzielone pojedynczym odstępem, 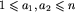 oraz
oraz 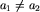 , oznaczające, odpowiednio, początkowe pozycje agentów nr 1 i nr 2.
, oznaczające, odpowiednio, początkowe pozycje agentów nr 1 i nr 2.
W m następnych wierszach znajdują się pary liczb naturalnych a i b oddzielone pojedynczymi odstępami, 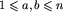 oraz
oraz 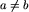 , oznaczające istnienie drogi z miasta a do miasta b.
, oznaczające istnienie drogi z miasta a do miasta b.
Plik tekstowy AGE.OUT powinien zawierać dokładnie 1 wiersz zawierający:
6 7 1 5 1 2 4 5 2 3 3 4 4 1 5 4 5 6poprawną odpowiedzią jest plik wyjściowy AGE.OUT
3
Sieć dróg Bajtocji reprezentujemy przez graf G o n wierzchołkach (miastach) i m krawędziach (drogach). Pierwszym, najbardziej narzucającym się rozwiązaniem, jest symulacja poruszania się obu agentów. Oznaczmy przez s=(i,j) stan obliczeń oznaczający, iż w tym samym czasie pierwszy agent może znajdować się w mieście o numerze i, a drugi w mieście o numerze j. Teraz rozważmy graf G' zbudowany na stanach s, ma on n2 wierzchołków i m2 krawędzi. W przypadku posługiwania się grafem G' problem sprowadza się do znalezienia najkrótszej ścieżki z wyróżnionego wierzchołka s_0=(a_1,a_2) do dowolnego wierzchołka postaci (i,i). Ponieważ wszystkie krawędzie mają wagę 1, więc wystarczy przejść graf G' wszerz. Nie trzeba konstruować grafu G' wprost, można także, jak w poniższym przykładzie, dynamicznie generować jego krawędzie.
| 1 | Q:={a_1,a_2}; |
| 2 | { początkowo, dla dowolnego i, j: v[i,j]=0 } |
| 3 | v[a_1,a_2]:=1; |
| 4 | t:=0; |
| 5 | while not Q.pusta do begin |
| 6 | Q2:=pusta_kolejka; |
| 7 | while not Q.pusta do begin |
| 8 | (u,v):=Q.PobierzElement; |
| 9 | if (u=v) then |
| 10 | ``Znaleziono rozwiązanie - t'' |
| 11 | STOP; |
| 12 | for i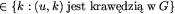 do do |
| 13 | for j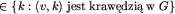 do do |
| 14 | if v[i,j]=0 then begin |
| 15 | v[i,j]:=1; |
| 16 | Q2.Dodaj(i,j); |
| 17 | end |
| 18 | end; |
| 19 | t:=t+1; |
| 20 | Q:=Q2; |
| 21 | end; |
| 22 | ``Brak rozwiązania'' |
Schemat algorytmu (Q i Q2 oznaczają kolejki typu "pierwszy wchodzi-pierwszy wychodzi", czyli FIFO):
Teraz zastanówmy się jaką złożoność ma powyższy algorytm. Oznaczmy przez K(i,j) koszt jaki trzeba ponieść aby wygenerować następniki stanu (i,j). Wówczas 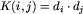 , gdzie dl oznacza liczbę krawędzi wychodzących z wierzchołka l. Ponieważ w pesymistycznym przypadku trzeba będzie rozpatrzyć wszystkie stany, całkowity koszt może wynosić:
, gdzie dl oznacza liczbę krawędzi wychodzących z wierzchołka l. Ponieważ w pesymistycznym przypadku trzeba będzie rozpatrzyć wszystkie stany, całkowity koszt może wynosić:
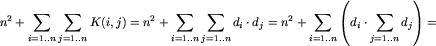
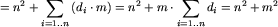
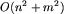 .
.
Rozwiązanie wzorcowe polega na pewnym ulepszeniu poprzedniego rozwiązania. W poprzednim rozwiązaniu jedna faza algorytmu polegała na wykonaniu ruchu oboma agentami. Tym razem podzielimy tą fazę na dwie części: ruch pierwszym agentem i ruch drugim agentem. Co prawda takie rozwiązanie dwukrotnie powiększa przestrzeń stanów: s=(i,j) (ten sam stan co w poprzednim rozwiązaniu), oraz dochodzą nowe stany s'=(i',j'), oznaczające, że pierwszy agent wykonał już swój ruch i znajduje się na pozycji i', natomiast drugi powinien teraz wykonać ruch, a na razie znajduje się na pozycji j'. Jednak dzięki tej metodzie znajdowanie następników stanów jest nieco mniej kosztowne, dla stanów s=(i,j) potrzeba di operacji, natomiast dla stanów s'=(i',j') potrzeba 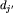 operacji. Tak jak w poprzednim algorytmie, dotarcie do stanu s=(i,i) oznacza, że agenci mogą zorganizować bezpieczne spotkanie.
operacji. Tak jak w poprzednim algorytmie, dotarcie do stanu s=(i,i) oznacza, że agenci mogą zorganizować bezpieczne spotkanie.
| 1 | Q:={a_1,a_2}; |
| 2 | { początkowo, dla dowolnego i, j: v[i,j]=0, oraz v'[i,j]=0 } |
| 3 | v[a_1,a_2]:=1; |
| 4 | t:=0; |
| 5 | while not Q.pusta do begin |
| 6 | Q2:=pusta_kolejka; |
| 7 | |
| 8 | {ruch pierwszego agenta} |
| 9 | while not Q.pusta do begin |
| 10 | (u,v):=Q.PobierzElement; |
| 11 | if (u=v) then |
| 12 | ``Znaleziono rozwiązanie - t'' |
| 13 | STOP; |
| 14 | for i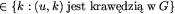 do do |
| 15 | if v'[i,v]=0 then begin |
| 16 | v'[i,v]:=1; |
| 17 | Q2.Dodaj(i,v) |
| 18 | end |
| 19 | end; |
| 20 | |
| 21 | {ruch drugiego agenta} |
| 22 | while not Q2.pusta do begin |
| 23 | (u,v):=Q2.PobierzElement; |
| 24 | for i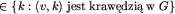 do do |
| 25 | if v[u,i]=0 then begin |
| 26 | v[u,i]:=1; |
| 27 | Q.Dodaj(i,v) |
| 28 | end |
| 29 | end; |
| 30 | |
| 31 | t:=t+1 |
| 32 | end; |
| 33 | ``Brak rozwiązania'' |
Teraz już możemy naszkicować schemat algorytmu (Q i Q2 oznaczają kolejki typu "pierwszy wchodzi-pierwszy wychodzi", czyli FIFO):
Niech K(i,j) oznacza koszt poniesiony na znalezienie następników stanu s=(i,j). Tak więc K(i,j)=d_i. Analogicznie K'(i,j) oznacza koszt dla stanów typu s'=(i',j'), a zatem K'(i,j)=d_j. W pesymistycznym przypadku łączny koszt całego algorytmu wynosi:
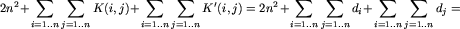
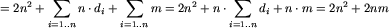
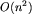 krawędzi)
krawędzi) 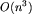 operacji.
operacji.
Innym rozwiązaniem, mającym złożoność O(dm), gdzie d oznacza minimalny czas potrzebny do zorganizowania bezpiecznego spotkania (lub n2, jeśli takiego spotkania nie można zorganizować), jest obliczanie do jakich miast mogą dojść w i-tym kroku agenci nr 1 i 2. Jeśli te dwa zbiory mają część wspólną, oznacza to możliwość spotkania w i-tym dniu.
Niestety w niektórych przypadkach czas potrzebny do zoorganizowania spotkania może być bardzo duży, nawet rzędu n2. Tak więc w pesymistycznych przypadkach to rozwiązanie jest równie wolne jak pierwsze.
| 1 | V1:={a_1}; |
| 2 | V2:={a_2}; |
| 3 | dl:=0; |
| 4 | while (not V1.pusty and not V2.pusty and 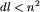 ) do ) do |
| 5 | begin |
| 6 | dl:=dl+1; |
| 7 | jeśli istnieje wierzchołek v należący do V1 i V2 |
| 8 | to ``Znaleziono rozwiązanie''; |
| 9 | V1:=wierzchołki v takie, że istnieje wierzchołek u  V1 V1 |
| 10 | i (u,v) należy do G; |
| 11 | V2:=wierzchołki v takie, że istnieje wierzchołek u  V2 V2 |
| 12 | i (u,v) należy do G |
| 13 | end; |
| 14 | ``Brak rozwiązania'' |
(Zmienne V1 i V2 oznaczają zbiory)
Do sprawdzania rozwiązań zawodników użyto 16 testów:
Testy oznaczone K_2(b_1,b_2,n) oznaczają testy składające się z dwóch pełnych grafów skierowanych (o rozmiarach b1, b2) połączonych ścieżką długości n
Testy oznaczone E(n_1,n_2,b_1,b_2) oznaczają testy składające się z dwóch pełnych grafów skierowanych (o rozmiarach b1, b2) połączone dwoma ścieżkami o wspólnym końcu, różniącymi się długością o 1. Na ścieżkach tych występują dodatkowo cykle długości n1, n2.
Testy 11 i 12 oraz 14 i 15 zostały zgrupowane.