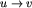 , albo
, albo 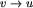 ),
), 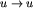 ).
).
Turniejem nazywamy graf skierowany, w którym:
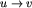 , albo
, albo 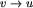 ),
), 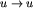 ).
).
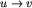 jest krawędzią w turnieju wtedy i tylko wtedy, gdy
jest krawędzią w turnieju wtedy i tylko wtedy, gdy 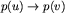 jest krawędzią w tym turnieju). Dla zadanej permutacji p interesuje nas, dla ilu turniejów jest ona automorfizmem.
jest krawędzią w tym turnieju). Dla zadanej permutacji p interesuje nas, dla ilu turniejów jest ona automorfizmem.
Weźmy zbiór wierzchołków oznaczonych liczbami 1,...,4 oraz permutację p:


Napisz program, który:
W pierwszym wierszu pliku tekstowego AUT.IN znajduje się jedna liczba naturalna n, 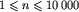 , będąca liczbą wierzchołków.
, będąca liczbą wierzchołków.
W kolejnych n wierszach znajduje się opis permutacji p. Zakładamy, że wierzchołki są ponumerowane liczbami od 1 do n. W wierszu (k+1)-szym znajduje się wartość permutacji p dla wierzchołka nr k (tzn. wartość p(k)).
W pierwszym i jedynym wierszu pliku tekstowego AUT.OUT powinna znaleźć się jedna liczba całkowita będąca resztą z dzielenia przez 1 000 liczby różnych n-wierzchołkowych turniejów, dla których permutacja p jest automorfizmem.
4 2 4 3 1poprawną odpowiedzią jest plik wyjściowy AUT.OUT
4
 - każdą parę liczb będziemy utożsamiać z parą wierzchołków o odpowiednich numerach. Pokażemy, że:
- każdą parę liczb będziemy utożsamiać z parą wierzchołków o odpowiednich numerach. Pokażemy, że: phCyklem permutacji p będziemy nazywać k-elementowy ciąg różnych liczb 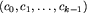 taki, że
taki, że 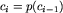 , dla
, dla 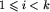 i
i 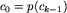 . Łatwo pokazać, że każdą permutację można przedstawić w postaci zbioru rozłącznych cykli.
. Łatwo pokazać, że każdą permutację można przedstawić w postaci zbioru rozłącznych cykli.
Dla przykładu permutacja p:


Liczbę s gromad wyznaczonych przez daną permutację p można szybko znaleźć, znając rozbicie permutacji na cykle.
Weźmy cykl C o długości k oraz należące do niego elementy u i v. Połóżmy biały żeton na u i czerwony żeton na v. Jeśli oba żetony jednocześnie przesuniemy po cyklu o jeden element, to dostaniemy parę zależną od 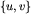 . Aby wyznaczyć wszystkie takie pary powtarzamy ten ruch tak długo, aż oba żetony z powrotem znajdą się na pozycjach startowych u i v.
. Aby wyznaczyć wszystkie takie pary powtarzamy ten ruch tak długo, aż oba żetony z powrotem znajdą się na pozycjach startowych u i v.
Zauważmy, że jeśli długość cyklu k jest liczbą parzystą i v jest odległe o  od u na cyklu C, to po k/2 krokach czerwony żeton znajdzie się na u, a biały - na v. To oznacza sprzeczność -
od u na cyklu C, to po k/2 krokach czerwony żeton znajdzie się na u, a biały - na v. To oznacza sprzeczność - 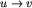 jest krawędzią w turnieju wtedy i tylko wtedy, gdy
jest krawędzią w turnieju wtedy i tylko wtedy, gdy 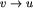 jest krawędzią w tym turnieju. W takim przypadku nie istnieje żaden turniej, dla którego permutacja p byłaby automorfizmem - ostateczną odpowiedzią jest liczba 0. Dalej będziemy zakładać, że wszystkie cykle są nieparzystej długości.
jest krawędzią w tym turnieju. W takim przypadku nie istnieje żaden turniej, dla którego permutacja p byłaby automorfizmem - ostateczną odpowiedzią jest liczba 0. Dalej będziemy zakładać, że wszystkie cykle są nieparzystej długości.
Jeśli długość cyklu jest liczbą nieparzystą, to niezależnie od tego jak wybraliśmy u i v, do początkowego ustawienia żetonów powrócimy po k krokach. Liczba k jest zatem licznością dowolnej gromady złożonej z par elementów cyklu C. Zbiór różnych par elementów cyklu C ma k(k-1)/2 elementów, zatem rozpada się na (k-1)/2 gromad.
Niech teraz u będzie elementem cyklu C o długości k, a v - elementem cyklu D długości l. Połóżmy znowu biały żeton na u, a czerwony na v. Aby wyznaczyć pary zależne od 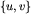 , podobnie jak poprzednio synchronicznie przesuwamy żetony, tym razem po rozłącznych cyklach. Po ilu krokach wrócimy do sytuacji początkowej? Żeton biały wraca na u po k krokach, żeton czerwony wraca na v po l krokach, zatem musimy wykonać NWW(k, l) kroków. Wszystkich par o jednym elemencie z C i drugim z D jest kl, a wszystkie gromady utworzone z takich par są liczności NWW(k, l), więc mamy kl/NWW(k, l) = NWD(k, l) takich gromad.
, podobnie jak poprzednio synchronicznie przesuwamy żetony, tym razem po rozłącznych cyklach. Po ilu krokach wrócimy do sytuacji początkowej? Żeton biały wraca na u po k krokach, żeton czerwony wraca na v po l krokach, zatem musimy wykonać NWW(k, l) kroków. Wszystkich par o jednym elemencie z C i drugim z D jest kl, a wszystkie gromady utworzone z takich par są liczności NWW(k, l), więc mamy kl/NWW(k, l) = NWD(k, l) takich gromad.
Możemy już policzyć liczbę gromad, na które rozpada się zbiór wszystkich par. Musimy najpierw wyznaczyć długości wszystkich cykli permutacji p - tę operację można łatwo zaimplementować, by działała w czasie O(n) - a następnie posumować liczby gromad po wszystkich parach cykli, stosując wyżej wyprowadzone wzory. Ponieważ permutacja może mieć rzędu n cykli, nasz algorytm miałby złożoność czasową nie lepszą niż 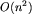 . Możemy jednak poprawić ten wynik poprzez zbiorowe traktowanie cykli o identycznych długościach. Niech ck oznacza liczbę cykli o długości k. Wtedy sumaryczna liczba gromad utworzonych przez pary o elementach pochodzących
. Możemy jednak poprawić ten wynik poprzez zbiorowe traktowanie cykli o identycznych długościach. Niech ck oznacza liczbę cykli o długości k. Wtedy sumaryczna liczba gromad utworzonych przez pary o elementach pochodzących
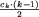 ,
, 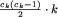 ,
, 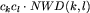 .
.
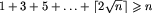 , różnych długości cykli jest co najwyżej
, różnych długości cykli jest co najwyżej 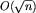 . Do rozpatrzenia mamy zatem O(n) par grup cykli różnych długości. Policzenie NWD(p, q) algorytmem Euklidesa zajmuje czas
. Do rozpatrzenia mamy zatem O(n) par grup cykli różnych długości. Policzenie NWD(p, q) algorytmem Euklidesa zajmuje czas 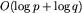 czasu (jego opis Czytelnik znajdzie w [13]), zatem otrzymujemy algorytm o złożoności czasowej
czasu (jego opis Czytelnik znajdzie w [13]), zatem otrzymujemy algorytm o złożoności czasowej 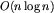 .
.
To nie koniec zadania, gdyż pozostaje nam jeszcze policzyć resztę z dzielenia 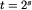 przez 1000. Kolejne potęgi dwójki będziemy naliczać iteracyjnie. Łatwo zauważyć, że przy wykonywaniu kolejnych mnożeń przez 2 wystarczy przechowywać jedynie resztę z dzielenia aktualnego wyniku przez 1000. Obserwacja ta jednak nie wystarcza, ponieważ s może być rzędu n2. Zauważmy jednak, że po wystarczająco dużej liczbie kroków (ale na pewno mniejszej niż 1000) trafimy w końcu na wartość, którą otrzymaliśmy już wcześniej. Niech i będzie właśnie takim najmniejszym wykładnikiem, że
przez 1000. Kolejne potęgi dwójki będziemy naliczać iteracyjnie. Łatwo zauważyć, że przy wykonywaniu kolejnych mnożeń przez 2 wystarczy przechowywać jedynie resztę z dzielenia aktualnego wyniku przez 1000. Obserwacja ta jednak nie wystarcza, ponieważ s może być rzędu n2. Zauważmy jednak, że po wystarczająco dużej liczbie kroków (ale na pewno mniejszej niż 1000) trafimy w końcu na wartość, którą otrzymaliśmy już wcześniej. Niech i będzie właśnie takim najmniejszym wykładnikiem, że 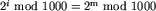 dla pewnego m < i. Wtedy dla każdego j > i mamy
dla pewnego m < i. Wtedy dla każdego j > i mamy
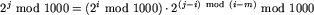
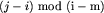 razy. Aby zrealizować ten algorytm potrzebna nam będzie 1000-elementowa tablica, w której r-tym elementem będzie wykładnik i, dla którego otrzymaliśmy resztę r.
razy. Aby zrealizować ten algorytm potrzebna nam będzie 1000-elementowa tablica, w której r-tym elementem będzie wykładnik i, dla którego otrzymaliśmy resztę r.
Algorytm ten wykona co najwyżej 2000 mnożeń, więc jego złożoność czasowa to O(1) (jest stała)!
Do sprawdzania rozwiązań zawodników użyto 12 testów. Testy 2 i 3 oraz 11 i 12 były zgrupowane. Permutacje z wszystkich testów, za wyjątkiem testu 2, zawierały wyłącznie cykle nieparzystych długości. Krótki opis testów zawarty jest poniżej: