Wojciech Guzicki (treść, opracowanie) Tomasz Waleń (program wzorcowy)
Gdzie zbudować browar?
Mieszkańcy bajtockiej wyspy Abstynencja bardzo lubią piwo bezalkoholowe.
Do tej pory piwo bezalkoholowe sprowadzano z Polski,
ale w tym roku w jednym z miast na Abstynencji
zostanie wybudowany browar. Wszystkie miasta wyspy leżą na wybrzeżu
i są połączone autostradą obiegającą wyspę wzdłuż brzegu.
Inwestor budujący browar zebrał informacje o zapotrzebowaniu
na piwo, tj. ile cystern piwa trzeba codziennie dostarczyć
do każdego z miast. Dysponuje także
zestawieniem odległości pomiędzy miastami.
Koszt transportu jednej cysterny na odległość 1 km wynosi 1 talar.
Dzienny koszt transportu to suma, jaką trzeba wyłożyć,
by do każdego miasta przetransportować z browaru tyle cystern,
ile wynosi zapotrzebowanie w danym mieście.
Jego wielkość zależy od miejsca położenia browaru.
Inwestor chce zminimalizować koszty transportu piwa.
Zadanie
Napisz program, który:
- wczyta z pliku tekstowego BRO.IN liczbę miast, odległości
między nimi oraz dzienne zapotrzebowania na piwo,
- obliczy minimalny dzienny koszt transportu piwa,
- zapisze wynik w pliku tekstowym BRO.OUT.
Wejście
W pierwszym wierszu pliku tekstowego BRO.IN jest zapisana jedna liczba
całkowita n równa liczbie miast, 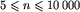 . W każdym z kolejnych
n wierszy zapisana jest para nieujemnych liczb całkowitych oddzielonych
pojedynczym odstępem.
Liczby z_i, d_i zapisane w (i+1)-ym wierszu, to, odpowiednio, zapotrzebowanie na piwo w mieście nr i oraz odległość (w kilometrach)
od miasta nr i do następnego miasta na autostradzie. Kolejne miasta na
autostradzie mają kolejne numery, po mieście nr n leży miasto nr 1.
Całkowita długość autostrady nie przekracza 1 000 000 km.
Zapotrzebowanie na piwo w żadnym mieście nie przekracza 1 000 cystern.
. W każdym z kolejnych
n wierszy zapisana jest para nieujemnych liczb całkowitych oddzielonych
pojedynczym odstępem.
Liczby z_i, d_i zapisane w (i+1)-ym wierszu, to, odpowiednio, zapotrzebowanie na piwo w mieście nr i oraz odległość (w kilometrach)
od miasta nr i do następnego miasta na autostradzie. Kolejne miasta na
autostradzie mają kolejne numery, po mieście nr n leży miasto nr 1.
Całkowita długość autostrady nie przekracza 1 000 000 km.
Zapotrzebowanie na piwo w żadnym mieście nie przekracza 1 000 cystern.
Wyjście
Twój program powinien zapisać w pierwszym i jedynym wierszu pliku tekstowego
BRO.OUT, dokładnie jedną liczbę całkowitą równą minimalnemu dziennemu
kosztowi transportu piwa.
Przykład
Dla pliku wejściowego BRO.IN
6
1 2
2 3
1 2
5 2
1 10
2 3
poprawną odpowiedzią jest plik wyjściowy BRO.OUT
41
Rozwiązanie
Oczywiste rozwiązanie polega na obliczeniu kosztu transportu z każdego miasta do każdego innego i dodaniu otrzymanych liczb. Dla każdego miasta należy obliczyć w tym celu n-1 odległości, co powoduje, że złożoność tego algorytmu wynosi 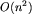 . Istnieje algorytm szybszy, działający w czasie O(n).
. Istnieje algorytm szybszy, działający w czasie O(n).
Warto zauważyć, że jeśli miasta są połączone siecią dróg będącą drzewem, to właściwa lokalizacja browaru nie zależy od odległości między miastami, ale tylko od zapotrzebowań w miastach. Oczywiście łączny koszt transportu zależy od odległości. Przypadek, gdy graf dróg jest drzewem (zresztą bardzo prostym), był już tematem jednego z zadań olimpijskich (Mudstok Bis, II Olimpiada Informatyczna, zobacz [2]). Jeśli graf dróg zawiera cykle, odpowiedź jest znacznie bardziej skomplikowana. Dla jednego cyklu istnieje algorytm liniowy, przy czym nie tylko łączny koszt, ale i lokalizacja browaru zależy teraz również od odległości.
Trudność polega na tym, że w drzewie istnieje tylko jedna droga prowadząca z danego miasta do każdego innego, natomiast w przypadku miast położonych na okręgu zawsze są dwie drogi: można obiegać okrąg w kierunku zgodnym z ruchem wskazówek zegara lub w kierunku przeciwnym. W przypadku każdej pary miast musimy zdecydować, który kierunek jest bardziej opłacalny. Przyjmijmy dla ustalenia uwagi, że miasta są numerowane w kierunku zgodnym z ruchem wskazówek zegara. Wczytane dane umieszczamy w dwóch tablicach: z[i] jest zapotrzebowaniem na piwo w mieście i, d[i] jest odległością od miasta i do następnego.
W algorytmie optymalnym najpierw obliczamy koszt transportu z miasta o numerze 1 (w programie wzorcowym dla wygody rozpoczęto numerację miast od zera; łatwiej wtedy obliczyć numer następnego i poprzedniego miasta na okręgu za pomocą funkcji mod). Jednocześnie obliczamy kilka wielkości pomocniczych:
- indeks l najdalszego miasta, do którego dowozimy piwo kierując się "w lewo", tzn. przeciwnie do ruchu wskazówek zegara;
- indeks r najdalszego miasta, do którego dowozimy piwo kierując się "w prawo", tzn. zgodnie z ruchem wskazówek zegara;
- łączne zapotrzebowanie zl na piwo w miastach, do których je dowozimy jadąc "w lewo";
- łączne zapotrzebowanie zr na piwo w miastach, do których je dowozimy jadąc "w prawo";
- odległość dl z pierwszego miasta do miasta o numerze l, gdy jedziemy "w lewo";
- odległość dr z pierwszego miasta do miasta o numerze r, gdy jedziemy "w prawo";
- łączny koszt transportu c - ten koszt zapamiętujemy jako dotychczas minimalny.
W kolejnych krokach algorytmu koszt transportu piwa z następnych miast będzie obliczany jako korekta obliczonego poprzednio kosztu. Przypuśćmy, że mamy obliczone te wszystkie dane dla miasta o numerze i-1. Wtedy dla miasta o numerze i dokonujemy prostej korekty. Najpierw znajdujemy odległość d między miastami o numerach i-1 oraz i. Następnie obliczamy, o ile zmieni się łączny koszt transportu piwa, jeśli będziemy je dowozić z miasta i po tych samych drogach: a więc do kosztu dodajemy ![(z_l+z[i-1])cdot d](img/blue28.png) i odejmujemy
i odejmujemy 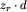 . Mianowicie wszystkie cysterny wysyłane w lewo przejadą odległość o d większą i dojdą nowe cysterny, które muszą dojechać do miasta o numerze i-1, a wszystkie cysterny jadące w prawo (w tym również te, które jechały do miasta i) przejadą o d mniej. Modyfikujemy również zl (dodając z[i-1]), zr (odejmując z[i]), dl (dodając d) i dr (odejmując d). Teraz poprawiamy łączny koszt, zwiększając liczbę cystern wysyłanych w prawo i zmniejszając liczbę cystern wysyłanych w lewo.
. Mianowicie wszystkie cysterny wysyłane w lewo przejadą odległość o d większą i dojdą nowe cysterny, które muszą dojechać do miasta o numerze i-1, a wszystkie cysterny jadące w prawo (w tym również te, które jechały do miasta i) przejadą o d mniej. Modyfikujemy również zl (dodając z[i-1]), zr (odejmując z[i]), dl (dodając d) i dr (odejmując d). Teraz poprawiamy łączny koszt, zwiększając liczbę cystern wysyłanych w prawo i zmniejszając liczbę cystern wysyłanych w lewo.
Patrzymy na odległość d[r] między miastem r i następnym leżącym na prawo (czyli zgodnie z ruchem wskazówek zegara) miastem l. Jeśli d_l>d_r+d[r], to do miasta o numerze l opłaca się teraz jechać w prawo. A więc dokonujemy kolejnej korekty: zwiększamy dr o d[r] i zr o z[r+1], zmniejszamy dl o d[l] i zl o z[l], zwiększamy o 1 numery miast r i l (pamiętając, że za n+1 bierzemy 1) i wreszcie odpowiednio modyfikujemy łączny koszt transportu. Teraz znów sprawdzamy, czy w podobny sposób nie przesunąć granicy między kierunkami w lewo i w prawo do następnego miasta. Postępujemy tak dotąd, aż dalsze zmiany nie przyniosą korzyści. W ten sposób zakończyliśmy korekty i mamy obliczony łączny koszt transportu piwa z miasta o numerze i. Porównujemy go z dotychczasowym minimalnym zapamiętując, jeśli jest mniejszy, i przechodzimy do kolejnego miasta.
Jaka będzie złożoność obliczeniowa tego algorytmu? Dla każdego miasta i dokonywaliśmy najpierw pewnej ustalonej liczby zmian, a następnie w pętli dokonywaliśmy być może wielu korekt. Zauważmy jednak, że każda z tych korekt dotyczyła zawsze nowej granicy między kierunkiem lewym i prawym, przy czym ta granica przesuwała się zawsze tylko w prawo. Zatem łącznie dokonaliśmy tylko n takich korekt. Stąd wynika, że czas działania tego algorytmu będzie proporcjonalny do n.
Dla liczby n=10000 różnica w czasie działania obu algorytmów (pierwszego o złożoności 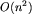 i drugiego o złożoności O(n)) jest znaczna i duże testy pozwalały na odrzucenie programów działających w czasie
i drugiego o złożoności O(n)) jest znaczna i duże testy pozwalały na odrzucenie programów działających w czasie 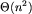 . Łączny koszt transportu mógł też przekroczyć zakres liczb typu longint i niektóre testy wykrywały ten błąd.
. Łączny koszt transportu mógł też przekroczyć zakres liczb typu longint i niektóre testy wykrywały ten błąd.
Testy
Do sprawdzania rozwiązań zawodników użyto 17 testów. Testy 1 i 2, 3 i 4, 5 i 6, 14 i 15 były grupowane.
BRO0.IN - przykładowy test z treści zadania,
BRO1.IN - n=10, mały test poprawnościowy,
BRO2.IN - n=15, mały test poprawnościowy,
BRO3.IN - n=20, test sprawdzający błąd przekroczenia zakresu,
BRO4.IN - n=20, pary mają postać (i,i),
BRO5.IN - n=30, mały test poprawnościowy,
BRO6.IN - n=40, mały test poprawnościowy,
BRO7.IN - n=500, na przemian pary (1,1), (100,1),
BRO8.IN - n=1000, na przemian pary (1,1), (100,1000),
BRO9.IN - n=3000, trzy grupy zawierające po 1000 miast oddalone o 300000 km,
BRO10.IN - n=4000, pary postaci ((i+1001) mod 1000, 100),
BRO11.IN - n=5000, pary postaci (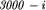 mod 1000, 100+(i mod 100)),
BRO12.IN - n=7000, pary mają postać ((i+1000) mod 1000, 100),
BRO13.IN - n=7500, dane losowe,
BRO14.IN - duży prosty test dla n=10000, wszystkie pary mają postać (1,1),
BRO15.IN - mały test poprawnościowy dla n=20,
BRO16.IN - n=10000, dane losowe.
mod 1000, 100+(i mod 100)),
BRO12.IN - n=7000, pary mają postać ((i+1000) mod 1000, 100),
BRO13.IN - n=7500, dane losowe,
BRO14.IN - duży prosty test dla n=10000, wszystkie pary mają postać (1,1),
BRO15.IN - mały test poprawnościowy dla n=20,
BRO16.IN - n=10000, dane losowe.
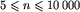 . W każdym z kolejnych
n wierszy zapisana jest para nieujemnych liczb całkowitych oddzielonych
pojedynczym odstępem.
Liczby z_i, d_i zapisane w (i+1)-ym wierszu, to, odpowiednio, zapotrzebowanie na piwo w mieście nr i oraz odległość (w kilometrach)
od miasta nr i do następnego miasta na autostradzie. Kolejne miasta na
autostradzie mają kolejne numery, po mieście nr n leży miasto nr 1.
Całkowita długość autostrady nie przekracza 1 000 000 km.
Zapotrzebowanie na piwo w żadnym mieście nie przekracza 1 000 cystern.
. W każdym z kolejnych
n wierszy zapisana jest para nieujemnych liczb całkowitych oddzielonych
pojedynczym odstępem.
Liczby z_i, d_i zapisane w (i+1)-ym wierszu, to, odpowiednio, zapotrzebowanie na piwo w mieście nr i oraz odległość (w kilometrach)
od miasta nr i do następnego miasta na autostradzie. Kolejne miasta na
autostradzie mają kolejne numery, po mieście nr n leży miasto nr 1.
Całkowita długość autostrady nie przekracza 1 000 000 km.
Zapotrzebowanie na piwo w żadnym mieście nie przekracza 1 000 cystern.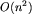 . Istnieje algorytm szybszy, działający w czasie O(n).
. Istnieje algorytm szybszy, działający w czasie O(n).![(z_l+z[i-1])cdot d](img/blue28.png) i odejmujemy
i odejmujemy 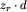 . Mianowicie wszystkie cysterny wysyłane w lewo przejadą odległość o d większą i dojdą nowe cysterny, które muszą dojechać do miasta o numerze i-1, a wszystkie cysterny jadące w prawo (w tym również te, które jechały do miasta i) przejadą o d mniej. Modyfikujemy również zl (dodając z[i-1]), zr (odejmując z[i]), dl (dodając d) i dr (odejmując d). Teraz poprawiamy łączny koszt, zwiększając liczbę cystern wysyłanych w prawo i zmniejszając liczbę cystern wysyłanych w lewo.
. Mianowicie wszystkie cysterny wysyłane w lewo przejadą odległość o d większą i dojdą nowe cysterny, które muszą dojechać do miasta o numerze i-1, a wszystkie cysterny jadące w prawo (w tym również te, które jechały do miasta i) przejadą o d mniej. Modyfikujemy również zl (dodając z[i-1]), zr (odejmując z[i]), dl (dodając d) i dr (odejmując d). Teraz poprawiamy łączny koszt, zwiększając liczbę cystern wysyłanych w prawo i zmniejszając liczbę cystern wysyłanych w lewo.
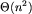 . Łączny koszt transportu mógł też przekroczyć zakres liczb typu longint i niektóre testy wykrywały ten błąd.
. Łączny koszt transportu mógł też przekroczyć zakres liczb typu longint i niektóre testy wykrywały ten błąd.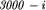 mod 1000, 100+(i mod 100)),
mod 1000, 100+(i mod 100)),