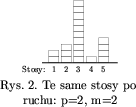
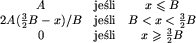W pewnej jednoosobowej grze ustawia się w rzędzie N stosów tak, że każdy z nich zawiera pewną liczbę (być może zero) krążków. Zobacz rysunek 1. Stosy są ponumerowane od 1 do N w ten sposób, że stosy 1 i N są na końcach. Ruch w tej grze polega na tym, że gracz wskazuje pewien stos, powiedzmy p, oraz podaje liczbę, powiedzmy m. Powoduje to przełożenie po m krążków ze stosu p na każdy z sąsiednich stosów. Zobacz przykład na rysunku 2. Stos p ma dwóch sąsiadów, p-1 oraz p+1, o ile 1 < p <N, ma sąsiada 2, gdy p=1, oraz sąsiada N-1, gdy p=N. Zauważ, że aby można było wykonać taki ruch, stos p musi zawierać co najmniej 2m krążków, jeśli ma dwóch sąsiadów i musi zawierać przynajmniej m krążków, jeśli ma tylko jednego sąsiada.
Celem gry jest "spłaszczenie" wszystkich stosów przez zrównanie liczb zawartych w nich krążków w możliwie najmniejszej liczbie ruchów. W przypadku gdy istnieje wiele rozwiązań, masz podać jedno z nich.
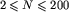
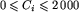, gdzie Ci to początkowa liczba krążków na stosie nr i (
).
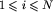Plikiem wejściowym jest plik tekstowy flat.inp. Zawiera on dwa wiersze.
Plikiem wyjściowym jest plik tekstowy flat.out.
flat.inp:
5 0 7 8 1 4
flat.out:
5 5 2 3 4 2 4 3 1 4 2
Limit na czas działania dla Twojego programu wynosi 3 sekundy.
Aby uzyskać pełną liczbę punktów, A, liczba Twoich ruchów, x, nie może przekraczać pewnej liczby B ustalonej przez program oceniający. B nie musi być równe minimalnej liczbie ruchów. W rzeczywistości B jest ustalane na podstawie liczby ruchów pewnej bardzo prostej strategii (unikającej zbędnych ruchów) oraz średniej liczby krążków na stosie. W tym zadaniu można otrzymać część punktów za pojedynczy test. Punkty, które otrzymasz zostaną wyliczone jako zaokrąglenie do najbliższej liczby całkowitej wartości określonej następującą formułą:
