Marcin Mucha (treść, opracowanie) Paweł Wolff (program wzorcowy)
Jajka
Wiadomo, że jajko zrzucone z wystarczająco dużej wysokości brzydko się rozbija. Dawniej wystarczyła wysokość jednego piętra, ale genetycznie podrasowane kury znoszą jajka nie tłukące się nawet po zrzuceniu z wysokości 100 000 000 pięter. Badania nad wytrzymałością jajek prowadzi się wykorzystując drapacze chmur. Opracowano specjalną skalę wytrzymałości jajek: jajko ma wytrzymałość k pięter, jeśli zrzucone z k-tego piętra nie rozbija się, ale zrzucone z (k+1)-ego już tak. W przypadku gdy drapacz chmur, którym dysponujemy, ma n pięter, przyjmujemy, że jajko rozbija się, gdy zrzucimy je z (n+1)-ego piętra. Przyjmujemy też, że każde jajko zrzucone z piętra o numerze 0 nie rozbija się.
Kierownik laboratorium postanowił wprowadzić oszczędności w procesie badawczym. Ograniczył on liczbę jajek, które wolno rozbić w trakcie eksperymentu mającego na celu ustalenie wytrzymałości jajek danego gatunku. Dodatkowo należy zminimalizować liczbę zrzutów jajek. Oznacza to, że mając do dyspozycji pewną liczbę jajek danego gatunku i drapacz chmur należy, w jak najmniejszej liczbie prób stwierdzić, jaka jest wytrzymałość jajek danego gatunku.
Zadanie
Twoim zadaniem jest napisanie modułu zawierającego trzy procedury (funkcje w przypadku języka C/C++):
- nowy_eksperyment - ta procedura będzie wywoływana na początku każdego nowego eksperymentu (może być ich więcej niż jeden);
- daj_pytanie - ta procedura służy do zadawania pytania, czy jajko wytrzyma zrzucenie z określonego piętra, czy też rozbije się; w tym celu należy w opisanej dalej zmiennej globalnej pietro umieścić numer piętra, z którego ma być zrzucone jajko,
- analizuj_odpowiedz - ta procedura powinna odczytać wartość zmiennej globalnej odpowiedz, która zawiera odpowiedź na ostatnio zadane pytanie (opis tej zmiennej znajduje się w kolejnym paragrafie) i dokonać analizy tej odpowiedzi - jeśli w wyniku tej analizy zostanie określona wytrzymałość jajka, to procedura ta powinna ten fakt zasygnalizować poprzez nadanie odpowiednich wartości zmiennym globalnym x oraz wiem (szczegóły znajdują się w kolejnym paragrafie).
Program nadzorujący przebieg eksperymentów wywoła napisaną przez Ciebie procedurę nowy_eksperyment na początku każdego nowego eksperymentu, po czym cyklicznie będzie wykonywał następujące czynności:
- wywołanie procedury daj_pytanie,
- odpowiadanie na pytanie,
- wywołanie procedury analizuj_odpowiedz,
aż do momentu, gdy Twój program stwierdzi, że zna wytrzymałość jajek gatunku używanego w danym eksperymencie (tzn. procedura analizuj_odpowiedz umieści odpowiednią wartość w zmiennej globalnej wiem).
Uwaga: Nie zakładaj, że program nadzorujący przebieg eksperymentów faktycznie ustala pewną wytrzymałość jajka przed rozpoczęciem danego eksperymentu. Może on dobierać ją w trakcie trwania eksperymentu w taki sposób, aby pasowała do wszystkich wcześniej udzielonych odpowiedzi oraz aby zmusić Twój program do zadania jak największej liczby pytań. Tak więc, powinieneś dążyć do tego, aby liczba pytań, jakie Twój program będzie musiał zadać w najgorszym przypadku, była jak najmniejsza.
Komunikacja
Komunikacja pomiędzy napisanym przez Ciebie modułem, a programem nadzorującym przebieg eksperymentów, odbywa się poprzez zmienne globalne.
Liczba pięter drapacza zapisana będzie w zmiennej globalnej wysokosc typu Longint (w przypadku języka C/C++ jest to typ long int). Będzie to dodatnia liczba całkowita, nie większa niż 100 000 000.
Maksymalna liczba jajek, które można stłuc w trakcie trwania eksperymentu zapisana będzie w zmiennej globalnej jajka typu Integer (w przypadku języka C/C++ jest to typ int). Będzie to dodatnia liczba całkowita, nie większa niż 1000.
Zadanie pytania, czy jajko wytrzyma zrzucenie z k-tego piętra, w procedurze daj_pytanie polega na przypisaniu zmiennej globalnej pietro typu Longint (w przypadku języka C/C++ jest to typ long int) liczby k.
Odpowiedź na zadane pytanie jest umieszczana w zmiennej globalnej odpowiedz typu Boolean (w przypadku języka C/C++ jest to typ int). Twierdzącej odpowiedzi na zadane pytanie (tzn. jajko wytrzyma) odpowiada wartość TAK, a przeczącej (tzn. jajko rozbije się) odpowiada NIE, gdzie TAK i NIE są stałymi o wartościach, odpowiednio, true i false (w przypadku języka C/C++ są to makra o wartościach, odpowiednio, 1 i 0).
W przypadku znalezienia wytrzymałości jajka Twój program powinien w procedurze analizuj_odpowiedz zapisać do zmiennej globalnej wiem typu Boolean (w przypadku języka C/C++ jest to typ int) TAK oraz w zmiennej globalnej x typu Longint (w przypadku języka C/C++ jest to typ long int) znalezioną wytrzymałość jajka.
Katalogi i pliki
Programujący w Pascalu powinni przygotowywać swoje rozwiązanie w katalogu JAJPAS, natomiast programujący w C i C++ w katalogu JAJC.
W katalogu JAJPAS (odpowiednio JAJC) znajdziesz następujące pliki:
- JAJmod.pas (odpowiednio JAJmod.h i JAJmod.c) - moduł zawierający definicje stałych TAK i NIE oraz deklaracje zmiennych globalnych,
- JAJ.pas - szkielet modułu znajdującego wytrzymałość jajka; powinieneś uzupełnić ten plik definicjami funkcji nowy_eksperyment, daj_pytanie i analizuj_odpowiedz (dla piszących w C lub C++ nagłówki powyższych funkcji znajdują się w pliku JAJ.h, musisz napisać plik JAJ.c lub JAJ.cpp z definicjami tych funkcji),
- test.pas (odpowiednio test.c) - przykładowy program nadzorujący przebieg eksperymentów i korzystający z Twojego modułu.
Wyjście
Wynikiem Twojej pracy powinien być zapisany na dyskietce tylko jeden plik: JAJ.pas, JAJ.c lub JAJ.cpp.
Rozwiązanie
Na początku eksperymentu wiemy, że wytrzymałość jajek danego gatunku mieści się w przedziale ![[0,tt wysokosc]](img/blue128.png) . Jeśli na pewnym etapie eksperymentu wiemy, że wytrzymałość mieści się w przedziale [a,b], to czego dowiemy się po zrzuceniu jajka z piętra o numerze p? Oczywiście będziemy wybierać
. Jeśli na pewnym etapie eksperymentu wiemy, że wytrzymałość mieści się w przedziale [a,b], to czego dowiemy się po zrzuceniu jajka z piętra o numerze p? Oczywiście będziemy wybierać 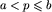 , gdyż dla innych wartości p jest jasne, czy jajko się rozbije, czy nie. W przypadku, gdy jajko się rozbije będziemy wiedzieli, że jego wytrzymałość zawiera się w przedziale [a,p-1]. Jeżeli natomiast jajko wytrzyma próbę, oznacza to, że jego wytrzymałość mieści się w przedziale [p,b]. Oczywiście eksperyment możemy zakończyć tylko wtedy, gdy długość przedziału, w jakim mieści się wytrzymałość jajek danego gatunku, wynosi 0. Zastanówmy się teraz, jak duży przedział wytrzymałości możemy sprawdzić mając do dyspozycji k jajek i n prób (tę maksymalną długość przedziału oznaczmy przez T(n,k)). Oczywiście mamy:
, gdyż dla innych wartości p jest jasne, czy jajko się rozbije, czy nie. W przypadku, gdy jajko się rozbije będziemy wiedzieli, że jego wytrzymałość zawiera się w przedziale [a,p-1]. Jeżeli natomiast jajko wytrzyma próbę, oznacza to, że jego wytrzymałość mieści się w przedziale [p,b]. Oczywiście eksperyment możemy zakończyć tylko wtedy, gdy długość przedziału, w jakim mieści się wytrzymałość jajek danego gatunku, wynosi 0. Zastanówmy się teraz, jak duży przedział wytrzymałości możemy sprawdzić mając do dyspozycji k jajek i n prób (tę maksymalną długość przedziału oznaczmy przez T(n,k)). Oczywiście mamy:
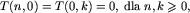 bo nie mając żadnych jajek lub prób, niewiele możemy zdziałać.
bo nie mając żadnych jajek lub prób, niewiele możemy zdziałać.
Jeżeli chcemy znaleźć wytrzymałość jajek pewnego gatunku w n próbach mając do dyspozycji k jajek i wiemy, że ich wytrzymałość mieści się w przedziale [a,b], to musimy zrzucić jajko z piętra o numerze nie większym niż a+T(n-1,k-1)+1 (w przeciwnym razie, w przypadku rozbicia jajka, pozostaje nam n-1 prób i k-1 jajek, lecz wytrzymałość mieści się w przedziale, którego długość jest większa niż T(n-1,k-1)) oraz nie mniejszym niż b-T(n-1,k) (w przeciwnym razie, w przypadku, gdy jajko wytrzyma próbę, pozostaje nam n-1 prób i k jajek, lecz wytrzymałość mieści się w przedziale o długości większej niż T(n-1,k)). Aby oba te warunki mogły być spełnione, długość przedziału [a,b] nie może być większa od T(n-1,k-1)+1+T(n-1,k). W takim przypadku, jajko można zrzucić z piętra o numerze min(a+T(n-1,k-1)+1,b), a zatem:
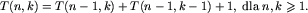 Ta formuła bardzo przypomina poniższą:
Ta formuła bardzo przypomina poniższą: 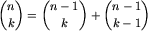
To sugeruje nam zbadanie związku liczb T(n,k) ze współczynnikami dwumianowymi 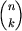 . Łatwo sprawdzić (troszkę trudniej zgadnąć), że:
. Łatwo sprawdzić (troszkę trudniej zgadnąć), że:
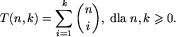 Porównując zapisy różnych T(n,k) łatwo otrzymujemy:
Porównując zapisy różnych T(n,k) łatwo otrzymujemy:
-
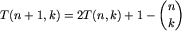 , dla
, dla 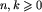 ;
;
-
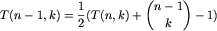 , dla
, dla 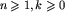 ;
;
-
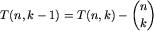 , dla
, dla 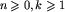 .
.
Przy pomocy wzoru (1) możemy wyznaczyć najmniejsze n takie, że 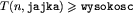 . Jest to, jak łatwo zauważyć, minimalna liczba prób jaka wystarcza do wyznaczenia wytrzymałości jajek w danym eksperymencie. Czas wyznaczenia liczby n jest oczywiście liniowy ze względu na tę liczbę. Przy pomocy wzorów (2), (3) możemy z kolei wyznaczyć w czasie stałym numer piętra, z którego należy zrzucić jajko (szczegóły można znaleźć w treści programu).
. Jest to, jak łatwo zauważyć, minimalna liczba prób jaka wystarcza do wyznaczenia wytrzymałości jajek w danym eksperymencie. Czas wyznaczenia liczby n jest oczywiście liniowy ze względu na tę liczbę. Przy pomocy wzorów (2), (3) możemy z kolei wyznaczyć w czasie stałym numer piętra, z którego należy zrzucić jajko (szczegóły można znaleźć w treści programu).
Jak liczyć symbole Newtona
Rozwiązanie wzorcowe wydaje się proste do zaprogramowania. Jest w nim jednak pewien haczyk. Na przykład, w jaki sposób obliczać 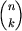 znając
znając 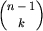 ? Nie możemy po prostu pomnożyć przez n i podzielić przez n-k, bo przekroczymy zakres. Można jednak poradzić sobie z tym problemem stosując częściowe dzielenie. Wiemy, że wynik naszych obliczeń będzie liczbą całkowitą. Można więc w ułamku
? Nie możemy po prostu pomnożyć przez n i podzielić przez n-k, bo przekroczymy zakres. Można jednak poradzić sobie z tym problemem stosując częściowe dzielenie. Wiemy, że wynik naszych obliczeń będzie liczbą całkowitą. Można więc w ułamku 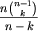 skrócić najpierw lewą część (
skrócić najpierw lewą część (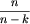 ), a potem prawą (szczegóły można znaleźć w treści programu).
), a potem prawą (szczegóły można znaleźć w treści programu).
Inne rozwiązania
Czy można uniknąć zgadywania tajemniczego wzoru na T(n,k)? Chyba tak. Możemy przecież wyliczać T(n,k) z formuły rekurencyjnej:
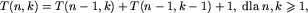
tzn. obliczać 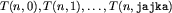 dla kolejnych n, aż
dla kolejnych n, aż
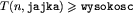 . Następnie postępować tak, jak w rozwiązaniu wzorcowym, przy czym jeśli mamy policzone wartości
. Następnie postępować tak, jak w rozwiązaniu wzorcowym, przy czym jeśli mamy policzone wartości
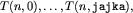 to
to 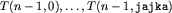 możemy uzyskać z wzoru:
możemy uzyskać z wzoru: 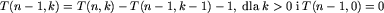 (oczywiście można pamiętać wszystkie wyliczone wartości i wtedy korzystanie z powyższego wzoru nie jest konieczne).
(oczywiście można pamiętać wszystkie wyliczone wartości i wtedy korzystanie z powyższego wzoru nie jest konieczne).
Jaka jest złożoność takiego algorytmu? Oczywiście 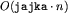 , gdzie n jest najmniejszą taką liczbą, że
, gdzie n jest najmniejszą taką liczbą, że 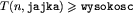 . Pozostaje pytanie: jak duże może być n? Można znaleźć dość dobre oszacowanie korzystając z mądrych wzorów, wystarczy jednak prosty rachunek, aby się przekonać, że iloczyn
. Pozostaje pytanie: jak duże może być n? Można znaleźć dość dobre oszacowanie korzystając z mądrych wzorów, wystarczy jednak prosty rachunek, aby się przekonać, że iloczyn 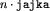 nigdy nie jest zbyt duży.
nigdy nie jest zbyt duży.
Jeśli 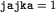 , to oczywiście
, to oczywiście 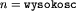 . Ten przypadek można jednak rozpatrywać osobno. Wystarczy rzucać jajko z kolejnych pięter.
. Ten przypadek można jednak rozpatrywać osobno. Wystarczy rzucać jajko z kolejnych pięter.
Jeśli 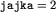 , to mamy:
, to mamy:
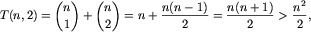 a więc wystarczy
a więc wystarczy 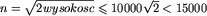 , co daje łącznie
, co daje łącznie 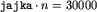 operacji.
operacji.
Dla 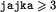 mamy:
mamy:
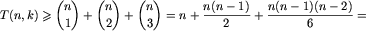
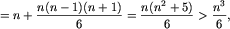
a więc wystarczy 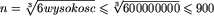 i łącznie najwyżej
i łącznie najwyżej 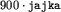 operacji. To już jest dobra złożoność, ale oczywiście można przeprowadzić podobny prosty rachunek dla
operacji. To już jest dobra złożoność, ale oczywiście można przeprowadzić podobny prosty rachunek dla 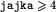 i otrzymać jeszcze lepsze oszacowanie.
i otrzymać jeszcze lepsze oszacowanie.
Opis działania programu arbitra
Arbiter oszukuje
Arbiter wcale nie ustala na początku eksperymentu wytrzymałości jajka. Wczytuje natomiast z pliku testowego przedział [min..max] wytrzymałości dopuszczalnych. Oznacza to z grubsza tyle, że jego odpowiedzi mają się zgadzać z pewną wytrzymałością z tego przedziału. Przykładowo, jeśli min=max, to arbiter faktycznie ustala na początku eksperymentu wytrzymałość jajka
Arbiter jest złośliwy
Arbiter nie ma wyboru przy udzielaniu odpowiedzi na pytanie, czy jajko zrzucone z k-tego piętra rozbije się, gdy 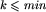 lub k>max. W przeciwnym razie, jeśli któraś z odpowiedzi wymusi na module zawodnika zadanie większej liczby pytań niż jest to konieczne, to taka odpowiedź jest udzielana. Jeśli zaś przy obu odpowiedziach moduł zawodnika zachowuje szansę na wyznaczenie wytrzymałości jajek w odpowiedniej liczbie prób, to udzielana jest odpowiedź wymuszająca na module zawodnika zadanie co najmniej minimalnej wystarczającej liczby pytań. Jeśli obie odpowiedzi wymuszają zadanie co najmniej minimalnej wystarczającej liczby pytań, to udzielana jest odpowiedź losowa. Jeśli żadna odpowiedź nie ma tej właściwości (może się tak zdażyć wtedy, gdy liczby min i max różnią się mało, a zawodnik "wstrzeli" się w przedział [min,max]), to udzielana jest odpowiedź TAK.
lub k>max. W przeciwnym razie, jeśli któraś z odpowiedzi wymusi na module zawodnika zadanie większej liczby pytań niż jest to konieczne, to taka odpowiedź jest udzielana. Jeśli zaś przy obu odpowiedziach moduł zawodnika zachowuje szansę na wyznaczenie wytrzymałości jajek w odpowiedniej liczbie prób, to udzielana jest odpowiedź wymuszająca na module zawodnika zadanie co najmniej minimalnej wystarczającej liczby pytań. Jeśli obie odpowiedzi wymuszają zadanie co najmniej minimalnej wystarczającej liczby pytań, to udzielana jest odpowiedź losowa. Jeśli żadna odpowiedź nie ma tej właściwości (może się tak zdażyć wtedy, gdy liczby min i max różnią się mało, a zawodnik "wstrzeli" się w przedział [min,max]), to udzielana jest odpowiedź TAK.
Oczywiście jeśli arbiter odpowiedział, że jajko zbije się po zrzuceniu z piętra k < max, to od tego momentu max=k-1. Analogicznie arbiter musi zwiększyć min, jeśli odpowiedział, że jajko się nie bije i k > min.
Arbiter wie wszystko
No dobrze, ale w jaki sposób można stwierdzić, czy po udzieleniu konkretnej odpowiedzi zawodnik będzie miał szansę na zmieszczenie się w minimalnej wystarczającej liczbie pytań? Można to zrobić, jeśli zna się wartości T(n,k). Arbiter wylicza te wartości w taki sam sposób, jak moduł wzorcowy.
Diabelska strategia arbitra
Jak już zaznaczyliśmy na wstępie, przypadek min=max jest wyjątkowo łagodny dla zawodnika. Na drugim biegunie leży przypadek min=0, max=wysokosc. W tej sytuacji arbiter nie jest w żaden sposób ograniczony i gładko wymusza na module zawodnika, aby ten zadał możliwie najwięcej pytań. Ten przypadek będziemy nazywać diabelską strategią arbitra.
Czy arbiter gra w kości?
W niektórych przypadkach arbiter udziela odpowiedzi losowych. Czy to oznacza, że ten sam deterministyczny moduł uruchomiony dwa razy może uzyskać dwie różne liczby punktów? To zdecydowanie nie byłoby dobrze. Dlatego arbiter z pliku testowego oprócz wartości min i max wczytuje ciąg 100 losowych bitów, z którego korzysta przy udzielaniu odpowiedzi.
Testy
Do sprawdzania rozwiązań zawodników użyto 11 testów, których opisy znajdują się poniżej.
JAJ1.IN - małe wysokości drapacza, mało jajek, uczciwy arbiter,
JAJ2.IN - średnie wysokości drapacza, różna liczba jajek, uczciwy arbiter,
JAJ3.IN - małe wysokości drapacza, mało jajek, średniej trudności strategia udzielania odpowiedzi przez arbitra,
JAJ4.IN - średnie wysokości drapacza, różna liczba jajek, średniej trudności strategia udzielania odpowiedzi przez arbitra,
JAJ5.IN - duże wysokości drapacza, różna liczba jajek, średniej trudności strategia udzielania odpowiedzi przez arbitra,
JAJ6.IN - małe wysokości drapacza, mało jajek, strategia diabelska,
JAJ7.IN - średnie wysokości drapacza, różna liczba jajek, strategia diabelska,
JAJ8.IN - duże wysokości drapacza, różna liczba jajek, strategia diabelska,
JAJ9.IN - duże wysokości drapacza, różna liczba jajek, strategia diabelska,
JAJ10.IN - duże wysokości drapacza, różna liczba jajek, strategia diabelska.
![[0,tt wysokosc]](img/blue128.png) . Jeśli na pewnym etapie eksperymentu wiemy, że wytrzymałość mieści się w przedziale [a,b], to czego dowiemy się po zrzuceniu jajka z piętra o numerze p? Oczywiście będziemy wybierać
. Jeśli na pewnym etapie eksperymentu wiemy, że wytrzymałość mieści się w przedziale [a,b], to czego dowiemy się po zrzuceniu jajka z piętra o numerze p? Oczywiście będziemy wybierać 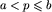 , gdyż dla innych wartości p jest jasne, czy jajko się rozbije, czy nie. W przypadku, gdy jajko się rozbije będziemy wiedzieli, że jego wytrzymałość zawiera się w przedziale [a,p-1]. Jeżeli natomiast jajko wytrzyma próbę, oznacza to, że jego wytrzymałość mieści się w przedziale [p,b]. Oczywiście eksperyment możemy zakończyć tylko wtedy, gdy długość przedziału, w jakim mieści się wytrzymałość jajek danego gatunku, wynosi 0. Zastanówmy się teraz, jak duży przedział wytrzymałości możemy sprawdzić mając do dyspozycji k jajek i n prób (tę maksymalną długość przedziału oznaczmy przez T(n,k)). Oczywiście mamy:
, gdyż dla innych wartości p jest jasne, czy jajko się rozbije, czy nie. W przypadku, gdy jajko się rozbije będziemy wiedzieli, że jego wytrzymałość zawiera się w przedziale [a,p-1]. Jeżeli natomiast jajko wytrzyma próbę, oznacza to, że jego wytrzymałość mieści się w przedziale [p,b]. Oczywiście eksperyment możemy zakończyć tylko wtedy, gdy długość przedziału, w jakim mieści się wytrzymałość jajek danego gatunku, wynosi 0. Zastanówmy się teraz, jak duży przedział wytrzymałości możemy sprawdzić mając do dyspozycji k jajek i n prób (tę maksymalną długość przedziału oznaczmy przez T(n,k)). Oczywiście mamy: 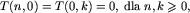
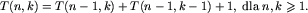
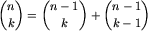
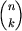 . Łatwo sprawdzić (troszkę trudniej zgadnąć), że:
. Łatwo sprawdzić (troszkę trudniej zgadnąć), że: 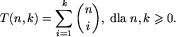
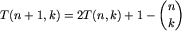 , dla
, dla 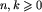 ;
;
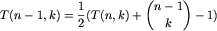 , dla
, dla 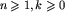 ;
;
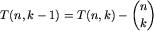 , dla
, dla 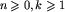 .
.
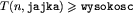 . Jest to, jak łatwo zauważyć, minimalna liczba prób jaka wystarcza do wyznaczenia wytrzymałości jajek w danym eksperymencie. Czas wyznaczenia liczby n jest oczywiście liniowy ze względu na tę liczbę. Przy pomocy wzorów (2), (3) możemy z kolei wyznaczyć w czasie stałym numer piętra, z którego należy zrzucić jajko (szczegóły można znaleźć w treści programu).
. Jest to, jak łatwo zauważyć, minimalna liczba prób jaka wystarcza do wyznaczenia wytrzymałości jajek w danym eksperymencie. Czas wyznaczenia liczby n jest oczywiście liniowy ze względu na tę liczbę. Przy pomocy wzorów (2), (3) możemy z kolei wyznaczyć w czasie stałym numer piętra, z którego należy zrzucić jajko (szczegóły można znaleźć w treści programu).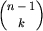 ? Nie możemy po prostu pomnożyć przez n i podzielić przez n-k, bo przekroczymy zakres. Można jednak poradzić sobie z tym problemem stosując częściowe dzielenie. Wiemy, że wynik naszych obliczeń będzie liczbą całkowitą. Można więc w ułamku
? Nie możemy po prostu pomnożyć przez n i podzielić przez n-k, bo przekroczymy zakres. Można jednak poradzić sobie z tym problemem stosując częściowe dzielenie. Wiemy, że wynik naszych obliczeń będzie liczbą całkowitą. Można więc w ułamku 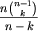 skrócić najpierw lewą część (
skrócić najpierw lewą część (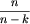 ), a potem prawą (szczegóły można znaleźć w treści programu).
), a potem prawą (szczegóły można znaleźć w treści programu).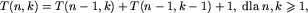
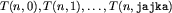 dla kolejnych n, aż
dla kolejnych n, aż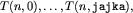
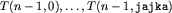
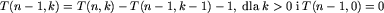
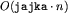 , gdzie n jest najmniejszą taką liczbą, że
, gdzie n jest najmniejszą taką liczbą, że 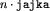 nigdy nie jest zbyt duży.
nigdy nie jest zbyt duży.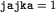 , to oczywiście
, to oczywiście 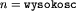 . Ten przypadek można jednak rozpatrywać osobno. Wystarczy rzucać jajko z kolejnych pięter.
. Ten przypadek można jednak rozpatrywać osobno. Wystarczy rzucać jajko z kolejnych pięter. , to mamy:
, to mamy: 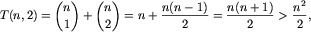
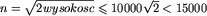 , co daje łącznie
, co daje łącznie 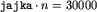 operacji.
operacji.
 mamy:
mamy: 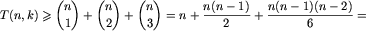
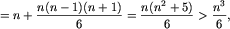
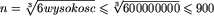 i łącznie najwyżej
i łącznie najwyżej 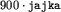 operacji. To już jest dobra złożoność, ale oczywiście można przeprowadzić podobny prosty rachunek dla
operacji. To już jest dobra złożoność, ale oczywiście można przeprowadzić podobny prosty rachunek dla 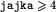 i otrzymać jeszcze lepsze oszacowanie.
i otrzymać jeszcze lepsze oszacowanie.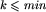 lub k>max. W przeciwnym razie, jeśli któraś z odpowiedzi wymusi na module zawodnika zadanie większej liczby pytań niż jest to konieczne, to taka odpowiedź jest udzielana. Jeśli zaś przy obu odpowiedziach moduł zawodnika zachowuje szansę na wyznaczenie wytrzymałości jajek w odpowiedniej liczbie prób, to udzielana jest odpowiedź wymuszająca na module zawodnika zadanie co najmniej minimalnej wystarczającej liczby pytań. Jeśli obie odpowiedzi wymuszają zadanie co najmniej minimalnej wystarczającej liczby pytań, to udzielana jest odpowiedź losowa. Jeśli żadna odpowiedź nie ma tej właściwości (może się tak zdażyć wtedy, gdy liczby min i max różnią się mało, a zawodnik "wstrzeli" się w przedział [min,max]), to udzielana jest odpowiedź TAK.
lub k>max. W przeciwnym razie, jeśli któraś z odpowiedzi wymusi na module zawodnika zadanie większej liczby pytań niż jest to konieczne, to taka odpowiedź jest udzielana. Jeśli zaś przy obu odpowiedziach moduł zawodnika zachowuje szansę na wyznaczenie wytrzymałości jajek w odpowiedniej liczbie prób, to udzielana jest odpowiedź wymuszająca na module zawodnika zadanie co najmniej minimalnej wystarczającej liczby pytań. Jeśli obie odpowiedzi wymuszają zadanie co najmniej minimalnej wystarczającej liczby pytań, to udzielana jest odpowiedź losowa. Jeśli żadna odpowiedź nie ma tej właściwości (może się tak zdażyć wtedy, gdy liczby min i max różnią się mało, a zawodnik "wstrzeli" się w przedział [min,max]), to udzielana jest odpowiedź TAK.