Krzysztof Diks, Marcin Kubica (przekład)
Światła drogowe
W mieście Dingilville wprowadzono niezwykły sposób sterowania ruchem ulicznym. Są tam skrzyżowania i łączące je drogi. Pomiędzy dowolnymi dwoma skrzyżowaniami jest co najwyżej jedna droga. Żadna droga nie łączy skrzyżowania z nim samym. Czas przejazdu każdą drogą jest taki sam dla obu kierunków jazdy. Na każdym skrzyżowaniu jest jedno światło, które w każdym momencie jest albo niebieskie, albo purpurowe. Światło na każdym skrzyżowaniu zmienia się cyklicznie: niebieskie świeci przez pewien okres czasu, a potem purpurowe przez pewien okres czasu, itd. Wolno przejechać drogą łączącą dwa skrzyżowania wtedy i tylko wtedy, gdy w momencie ruszania światła na obu tych skrzyżowaniach mają taki sam kolor. Jeżeli pojazd przyjeżdża na skrzyżowanie dokładnie w chwili zmiany świateł na skrzyżowaniu(-ach), musisz przyjąć nowe kolory świateł. Pojazdy mogą czekać na skrzyżowaniach. Masz plan miasta pokazujący:
- czasy przejazdu dla wszystkich dróg (liczby całkowite),
- czasy trwania kolorów świateł na każdym skrzyżowaniu (liczby całkowite),
- początkowy kolor światła i czas (liczba całkowita) pozostały do jego zmiany, dla każdego skrzyżowania.
Masz znaleźć sposób przejazdu w najkrótszym czasie, od zadanego skrzyżowania początkowego do zadanego skrzyżowania końcowego, zaczynając w momencie rozpoczęcia ruchu. W przypadku, gdy istnieje wiele takich sposobów przejazdu, masz podać tylko jeden z nich.
Założenia
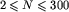 , gdzie N jest liczbą skrzyżowań. Skrzyżowania są ponumerowane od 1 do N. Numery te identyfikują skrzyżowania.
, gdzie N jest liczbą skrzyżowań. Skrzyżowania są ponumerowane od 1 do N. Numery te identyfikują skrzyżowania. 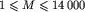 , gdzie M jest liczbą dróg.
, gdzie M jest liczbą dróg. 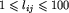 , gdzie lij jest czasem przejazdu drogą łączącą skrzyżowania i oraz j.
, gdzie lij jest czasem przejazdu drogą łączącą skrzyżowania i oraz j. 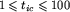 , gdzie tic jest czasem trwania światła koloru c na skrzyżowaniu i. Wartością c może być B dla koloru niebieskiego i P dla purpurowego.
, gdzie tic jest czasem trwania światła koloru c na skrzyżowaniu i. Wartością c może być B dla koloru niebieskiego i P dla purpurowego. 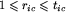 , gdzie ric jest czasem pozostałym do zmiany początkowego koloru c światła na skrzyżowaniu i.
, gdzie ric jest czasem pozostałym do zmiany początkowego koloru c światła na skrzyżowaniu i.
Wejście
Plik wejściowy jest plikiem tekstowym o nazwie lights.inp. - Pierwszy wiersz zawiera dwie liczby: numer skrzyżowania początkowego i numer skrzyżowania końcowego.
- Drugi wiersz zawiera dwie liczby: N, M.
- Następne N wierszy zawiera informacje o N skrzyżowaniach. (i+2)-gi wiersz pliku wejściowego zawiera informacje o skrzyżowaniu nr i: Ci, ric, tiB, tiP, gdzie Ci ma wartość 'B' lub 'P' oznaczającą początkowy kolor światła na skrzyżowaniu i.
- Dalsze M wierszy zawiera informacje o M drogach. Każdy wiersz ma postać: i, j, lij, gdzie i oraz j są numerami skrzyżowań, które dana droga łączy.
Wyjście
Plik wyjściowy jest plikiem tekstowym o nazwie lights.out. Jeśli istnieje sposób przejazdu:
- Pierwszy wiersz zawiera czas najkrótszego przejazdu od skrzyżowania początkowego do skrzyżowania końcowego.
- Drugi wiersz zawiera opis szukanego sposobu przejazdu - ciąg kolejnych skrzyżowań, przez które należy przejechać. W szczególności, pierwsza liczba w tym wierszu będzie numerem skrzyżowania początkowego, a ostatnia numerem skrzyżowania końcowego.
Jeśli szukany sposób przejazdu nie istnieje:
- Pojedynczy wiersz zawierający liczbę 0.
Przykład
lights.inp:
1 4
4 5
B 2 16 99
P 6 32 13
P 2 87 4
P 38 96 49
1 2 4
1 3 40
2 3 75
2 4 76
3 4 77
lights.out:
127
1 2 4
Ocena
Ograniczenie na czas działania Twojego programu wynosi 2s. Nie można uzyskać części punktów za pojedynczy test.
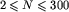 , gdzie N jest liczbą skrzyżowań. Skrzyżowania są ponumerowane od 1 do N. Numery te identyfikują skrzyżowania.
, gdzie N jest liczbą skrzyżowań. Skrzyżowania są ponumerowane od 1 do N. Numery te identyfikują skrzyżowania. 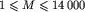 , gdzie M jest liczbą dróg.
, gdzie M jest liczbą dróg. 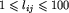 , gdzie lij jest czasem przejazdu drogą łączącą skrzyżowania i oraz j.
, gdzie lij jest czasem przejazdu drogą łączącą skrzyżowania i oraz j. 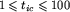 , gdzie tic jest czasem trwania światła koloru c na skrzyżowaniu i. Wartością c może być B dla koloru niebieskiego i P dla purpurowego.
, gdzie tic jest czasem trwania światła koloru c na skrzyżowaniu i. Wartością c może być B dla koloru niebieskiego i P dla purpurowego. 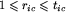 , gdzie ric jest czasem pozostałym do zmiany początkowego koloru c światła na skrzyżowaniu i.
, gdzie ric jest czasem pozostałym do zmiany początkowego koloru c światła na skrzyżowaniu i.