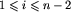 zachodzi:
zachodzi:W fabryce poduszkowców do budowy torów testowych używa się standardowych bloków o różnych wysokościach, ustawianych jeden za drugim. W idealnie zbudowanym torze, zwanym lollobrygidą, nigdy nie występują obok siebie dwa bloki jednakowej wysokości, nigdy też trzy kolejne bloki nie mają kolejno coraz większych, albo coraz mniejszych wysokości.
Mówiąc bardziej formalnie, niech h_1,... ,h_n oznacza ciąg wysokości kolejnych bloków należących do toru. Jeśli dla każdego 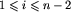 zachodzi:
zachodzi:
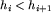 i
i 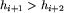 lub
lub 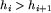 i
i 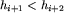 ,
,
Z zestawu 5 bloków o wysokościach 3, 3, 3, 5, 2 nie da się zbudować lollobrygidy, gdyż albo musiałyby stać w niej obok siebie dwa bloki wysokości 3, albo musi się w niej pojawić jedna z niedozwolonych sekwencji 2, 3, 5 lub 5, 3, 2.
A oto przykład lollobrygidy, poprawnie zbudowanej z innego zestawu bloków: 3, 2, 5, 2, 3, 1.
Z tego zestawu można też zbudować inne lollobrygidy.
Napisz program, który wczyta z pliku tekstowego LOL.IN liczbę zestawów danych i dla każdego zestawu:
W pierwszym wierszu pliku tekstowego LOL.IN znajduje się liczba całkowita d, 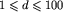 , równa liczbie zestawów danych. W następnym wierszu pliku LOL.IN zaczyna się pierwszy zestaw danych.
, równa liczbie zestawów danych. W następnym wierszu pliku LOL.IN zaczyna się pierwszy zestaw danych.
W pierwszym wierszu każdego zestawu danych znajduje się liczba całkowita n, 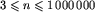 . Jest to liczba bloków w tym zestawie.
. Jest to liczba bloków w tym zestawie.
W kolejnych n wierszach znajdują się wysokości bloków. Każdy z tych wierszy zawiera jedną liczbę całkowitą h równą wysokości odpowiedniego bloku, 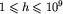 .
.
Kolejne zestawy danych następują bezpośrednio po sobie.
Plik tekstowy LOL.OUT powinien zawierać dokładnie d wierszy, po jednym dla każdego zestawu danych. W i-tym wierszu pliku LOL.OUT powinien być zapisany jeden wyraz:
2 5 3 3 3 5 2 6 3 3 1 5 2 2poprawną odpowiedzią jest plik wyjściowy LOL.OUT
NIE TAK
Zadanie o lollobrygidzie w dużej części sprowadzało się do znanego i opisywanego w literaturze zadania o wyborze lidera. Zadanie to formułuje się następująco: Stwierdzić, czy w ciągu  istnieje wartość, która występuje w nim więcej niż
istnieje wartość, która występuje w nim więcej niż  razy. Jeżeli taka wartość występuje, to nazywamy ją liderem.
razy. Jeżeli taka wartość występuje, to nazywamy ją liderem.
Okazuje się bowiem, że zachodzi następujące twierdzenie:
Twierdzenie. Z elementów  można ułożyć lollobrygidę wtedy i tylko wtedy, gdy zachodzi jeden z dwóch przypadków:
można ułożyć lollobrygidę wtedy i tylko wtedy, gdy zachodzi jeden z dwóch przypadków:
 nie występuje lider.
nie występuje lider.
 istnieje lider występujący w nim dokładnie
istnieje lider występujący w nim dokładnie 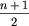 razy, a pozostałe elementy ciągu
razy, a pozostałe elementy ciągu  są albo wszystkie większe, albo wszystkie mniejsze od lidera.
są albo wszystkie większe, albo wszystkie mniejsze od lidera.
Dowód. Najpierw pokażemy, że jeżeli istnieje lider nie spełniający warunku (2), to lollobrygidy ułożyć się nie da, a potem, że jeśli ciąg spełnia którykolwiek z warunków (1) lub (2), to lollobrygidę ułożyć się da.
Załóżmy więc, że istnieje lider nie spełniający warunku (2). Jeżeli n jest parzyste, to lider występuje co najmniej 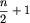 razy, zatem przy każdym ułożeniu wyrazów ciągu gdzieś dwaj liderzy muszą ze sobą sąsiadować. Jeśli bowiem podzielimy ciąg na dwuelementowe bloki (a jest ich dokładnie
razy, zatem przy każdym ułożeniu wyrazów ciągu gdzieś dwaj liderzy muszą ze sobą sąsiadować. Jeśli bowiem podzielimy ciąg na dwuelementowe bloki (a jest ich dokładnie  ), to z zasady szufladkowej Dirichleta wynika, że przynajmniej w jednym bloku znajdą się dwaj liderzy, więc podany ciąg nie będzie lollobrygidą.
), to z zasady szufladkowej Dirichleta wynika, że przynajmniej w jednym bloku znajdą się dwaj liderzy, więc podany ciąg nie będzie lollobrygidą.
Jeżeli n jest nieparzyste i lider występuje co najmniej 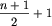 razy, to dzieląc ciąg
razy, to dzieląc ciąg  na bloki dwuelementowe, otrzymamy takich bloków
na bloki dwuelementowe, otrzymamy takich bloków 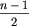 i zostanie jeszcze jeden blok jednoelementowy. Tak jak poprzednio, każda próba umieszczenia w takich blokach
i zostanie jeszcze jeden blok jednoelementowy. Tak jak poprzednio, każda próba umieszczenia w takich blokach 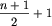 liderów musi się zakończyć tym, że dwaj liderzy znajdą się w jednym bloku obok siebie. Jeśli zaś n jest nieparzyste i lider występuje dokładnie
liderów musi się zakończyć tym, że dwaj liderzy znajdą się w jednym bloku obok siebie. Jeśli zaś n jest nieparzyste i lider występuje dokładnie 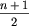 razy, ale nie jest najmniejszą, ani największą wartością, to co prawda można wszystkich liderów rozmieścić w
razy, ale nie jest najmniejszą, ani największą wartością, to co prawda można wszystkich liderów rozmieścić w 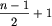 różnych blokach, ale żeby tor był lollobrygidą musimy umieścić ich wszystkich na nieparzystych pozycjach. Wtedy jednak na pewno wystąpi sytuacja, w której kolejne trzy wartości będą albo rosnące, albo malejące. Załóżmy bowiem dla symetrii, że a_2>a_1 (a1 jest wartością lidera). Wtedy a_4>a_3=a_1 (inaczej ciąg a_2,a_3,a_4 byłby malejący), a_6>a_5=a_1, itd. Okazałoby się więc, że a1 jest najmniejszą wartością wbrew założeniu. Analogicznie przeprowadzamy rozumowanie, jeśli a_2<a_1.
różnych blokach, ale żeby tor był lollobrygidą musimy umieścić ich wszystkich na nieparzystych pozycjach. Wtedy jednak na pewno wystąpi sytuacja, w której kolejne trzy wartości będą albo rosnące, albo malejące. Załóżmy bowiem dla symetrii, że a_2>a_1 (a1 jest wartością lidera). Wtedy a_4>a_3=a_1 (inaczej ciąg a_2,a_3,a_4 byłby malejący), a_6>a_5=a_1, itd. Okazałoby się więc, że a1 jest najmniejszą wartością wbrew założeniu. Analogicznie przeprowadzamy rozumowanie, jeśli a_2<a_1.
Pokazaliśmy więc pierwszą część twierdzenia. Pozostaje wykazać, że jeśli lidera nie ma lub jeśli jest lider, ale spełniający warunek (2), to lollobrygidę da się ułożyć z podanych wartości. Proste jest pokazanie, że jeśli lider spełnia warunek (2), to lollobrygidę daje się ułożyć. Wystarczy na wszystkich nieparzystych pozycjach ulokować lidera, a pozostałe elementy umieścić dowolnie na parzystych pozycjach. Warunek lollobrygidy w oczywisty sposób jest spełniony.
Zostało zatem do wykazania, że jeśli lidera nie ma, to lollobrygidę zawsze się da ułożyć. Dowód będzie indukcyjny ze względu na długość ciągu n.
Wzmocnimy najpierw nieco tezę - jest to częsty chwyt przy dowodach indukcyjnych; korzystamy przecież wtedy z mocniejszego założenia indukcyjnego. Pokażemy zatem, że jeśli lidera w ciągu  nie ma, to istnieje dla niego lollobrygida
nie ma, to istnieje dla niego lollobrygida  , i to taka, że
, i to taka, że 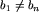 .
.
Bazę indukcji pokażemy dla wartości n=2. To nie szkodzi, że w sformułowaniu zadania 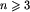 . Jeżeli uda się nam zacząć indukcję od mniejszej wartości - tym lepiej. Twierdzenie staje się trochę ogólniejsze, a zazwyczaj dla mniejszych wartości n łatwiej jest udowodnić bazę indukcji. Faktycznie, załóżmy, że w ciągu a_1,a_2 nie ma lidera. Wobec tego
. Jeżeli uda się nam zacząć indukcję od mniejszej wartości - tym lepiej. Twierdzenie staje się trochę ogólniejsze, a zazwyczaj dla mniejszych wartości n łatwiej jest udowodnić bazę indukcji. Faktycznie, załóżmy, że w ciągu a_1,a_2 nie ma lidera. Wobec tego 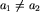 , zatem ciąg a_1,a_2 jest lollobrygidą: nie ma w nim ani dwóch sąsiadujących, równych sobie elementów, jak również żadne trzy sąsiednie elementy nie są posortowane - po prostu nie istnieją.
, zatem ciąg a_1,a_2 jest lollobrygidą: nie ma w nim ani dwóch sąsiadujących, równych sobie elementów, jak również żadne trzy sąsiednie elementy nie są posortowane - po prostu nie istnieją.
Załóżmy teraz, że teza zachodzi dla każdego ciągu  , k<n. Rozbijmy dowód na dwa przypadki: n nieparzyste i n parzyste.
, k<n. Rozbijmy dowód na dwa przypadki: n nieparzyste i n parzyste.
Najpierw n nieparzyste. Niech m będzie modą ciągu  . (Moda ciągu
. (Moda ciągu  jest to taka wartość, która w ciągu powtarza się najczęściej. Jeśli takich wartości jest więcej niż jedna, to każda z tych wartości jest modą. Lider oczywiście zawsze jest modą, ale nie na odwrót.) Usuńmy z ciągu
jest to taka wartość, która w ciągu powtarza się najczęściej. Jeśli takich wartości jest więcej niż jedna, to każda z tych wartości jest modą. Lider oczywiście zawsze jest modą, ale nie na odwrót.) Usuńmy z ciągu  jeden element - modę. W powstałym (n-1)-elementowym ciągu nie ma lidera, bo przy nieparzystym n, co najwyżej
jeden element - modę. W powstałym (n-1)-elementowym ciągu nie ma lidera, bo przy nieparzystym n, co najwyżej 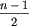 elementów ciągu mogło być równych modzie nie będącej liderem i żadna inna wartość nie mogła wystąpić w nim więcej razy.
elementów ciągu mogło być równych modzie nie będącej liderem i żadna inna wartość nie mogła wystąpić w nim więcej razy.
Taki ciąg po usunięciu jednego elementu będącego modą spełnia założenie indukcyjne: jest krótszy od n i nie zawiera lidera, zatem można z niego utworzyć lollobrygidę 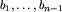 taką, że
taką, że 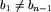 . Załóżmy, że b_1<b_2, a co za tym idzie,
. Załóżmy, że b_1<b_2, a co za tym idzie, 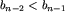 (n-1 jest parzyste, a kolejne wyrazy są na przemian od siebie większe i mniejsze). W przypadku odwrotnym, kiedy b_1>b_2 i
(n-1 jest parzyste, a kolejne wyrazy są na przemian od siebie większe i mniejsze). W przypadku odwrotnym, kiedy b_1>b_2 i 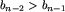 , rozumowanie będzie analogiczne. Jeśli teraz m>b_1, to wstawiając m przed ciąg
, rozumowanie będzie analogiczne. Jeśli teraz m>b_1, to wstawiając m przed ciąg 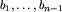 otrzymujemy lollobrygidę, jeśli nie, to sprawdzamy, czy
otrzymujemy lollobrygidę, jeśli nie, to sprawdzamy, czy 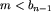 . Jeśli tak, to lollobrygidę otrzymamy wstawiając m na koniec. Pozostał więc przypadek
. Jeśli tak, to lollobrygidę otrzymamy wstawiając m na koniec. Pozostał więc przypadek 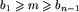 , przy czym jedna z tych nierówności musi być ostra. Wstawienie m z tej strony, z której nierówność jest ostra, między skrajny element, a jego sąsiada, spowoduje, że otrzymamy lollobrygidę o n elementach. To kończy dowód dla n nieparzystego.
, przy czym jedna z tych nierówności musi być ostra. Wstawienie m z tej strony, z której nierówność jest ostra, między skrajny element, a jego sąsiada, spowoduje, że otrzymamy lollobrygidę o n elementach. To kończy dowód dla n nieparzystego.
Jeśli n jest parzyste, to mamy trochę inną sytuację, bo usunięcie mody może doprowadzić nas do sytuacji, w której pojawi się lider w ciągu n-1-elementowym i nie będzie można skorzystać z założenia indukcyjnego. Poradzimy sobie z tym przypadkiem zauważając, że tak może być jedynie wtedy, gdy w ciągu występują tylko dwie wartości i każda z nich jest modą. Wtedy nie musimy stosować indukcji - wystarczy ustawić jedne wartości na nieparzystych, a drugie na parzystych miejscach i mamy lollobrygidę. W każdym innym przypadku po usunięciu z ciągu, w którym nie było lidera, jednego elementu o wartości mody, lidera nadal nie będzie. Możemy wtedy stosować założenie indukcyjne. Załóżmy więc, że ciąg 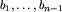 jest lollobrygidą taką, że
jest lollobrygidą taką, że 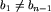 . Bez utraty ogólności możemy założyć, że b_1<b_2, a co za tym idzie,
. Bez utraty ogólności możemy założyć, że b_1<b_2, a co za tym idzie, 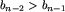 , gdyż n-1 jest nieparzyste. Przypadek przeciwny ma analogiczny dowód.
, gdyż n-1 jest nieparzyste. Przypadek przeciwny ma analogiczny dowód.
Jeżeli teraz m>b_1 lub 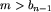 , to wstawiając m na początek lub odpowiednio na koniec, uzyskujemy lollobrygidę. Pozostaje zatem do rozważenia przypadek, gdy m nie przekracza żadnego ze skrajnych elementów. Ponieważ są one różne, więc m od jednego z nich musi być ostro mniejsze. Dajmy na to, że m<b_1. Wtedy wstawiając m między b1 a b2, otrzymujemy lollobrygidę. Analogicznie postępujemy, gdy
, to wstawiając m na początek lub odpowiednio na koniec, uzyskujemy lollobrygidę. Pozostaje zatem do rozważenia przypadek, gdy m nie przekracza żadnego ze skrajnych elementów. Ponieważ są one różne, więc m od jednego z nich musi być ostro mniejsze. Dajmy na to, że m<b_1. Wtedy wstawiając m między b1 a b2, otrzymujemy lollobrygidę. Analogicznie postępujemy, gdy 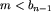 .
.
Wyczerpaliśmy tym samym wszystkie przypadki, za każdym razem pokazując, że lollobrygida jest możliwa do ułożenia. Twierdzenie zostało tym samym udowodnione.
Uff! Mamy już w ręku ważny wynik, który ułatwi rozwiązanie zadania w efektywny sposób. Pozostaje więc sprawdzić, czy lider istnieje i jeżeli nie, to odpowiedź jest TAK, a jeśli lider istnieje, to wystarczy upewnić się, czy nie spełnia warunku (2). Jeżeli spełnia, to odpowiedź jest TAK, a jeśli nie spełnia, to odpowiedź jest NIE.
Omówmy tu 4 różne algorytmy stwierdzania istnienia lidera.
Pierwszy algorytm, być może najprostszy do wymyślenia, polega na posortowaniu danych i znalezieniu w posortowanym ciągu najdłuższej sekwencji tych samych elementów. Koszt dobrego sortowania jest proporcjonalny do 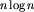 , koszt znalezienia najdłuższej stałej sekwencji jest proporcjonalny do n. Łącznie mamy więc algorytm o złożoności rzędu
, koszt znalezienia najdłuższej stałej sekwencji jest proporcjonalny do n. Łącznie mamy więc algorytm o złożoności rzędu 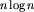 . Nieźle, ale nie optymalnie.
. Nieźle, ale nie optymalnie.
Drugi algorytm bazuje na spostrzeżeniu, że jeśli w ciągu jest lider, to jest on równy medianie ciągu, czyli elementowi, który w posortowanym ciągu wystąpiłby pośrodku (dla n parzystego jako medianę definiuje się dowolny z dwóch elementów środkowych). Algorytm zatem rozbija się na dwie części: wyznaczenie mediany i sprawdzenie, czy mediana jest liderem. Ta druga część jest bardzo prosta. Wyznaczenie mediany jest bardziej kłopotliwe, o ile nie chcemy korzystać z sortowania.
Medianę można wyznaczyć w czasie pesymistycznym proporcjonalnym do n, ale nie jest to proste. Zadanie to realizuje na przykład algorytm Bluma, Floyda, Pratta, Rivesta, Tarjana, zwany algorytmem piątek lub algorytmem pięciu - każda z nazw jest uzasadniona. Algorytm ten opisany jest np. w książce [10]. Problem polega na tym, że koszt tego algorytmu, choć liniowy, obarczony jest dużą stałą i dla potrzeb naszego zadania algorytm ten raczej się nie nadaje. Przy podanych ograniczeniach na rozmiar danych uzyskanie za pomocą tego algorytmu lepszego czasowo rozwiązania, niż przez sortowanie, wydaje się trudne, a być może jest wręcz niemożliwe. Pamiętajmy bowiem, że choć teoretycznie złożoność jednego algorytmu może być lepsza od złożoności drugiego, to wcale nie znaczy, że zawsze należy stosować ten pierwszy. Na przykład dla krótkich ciągów danych (rzędu kilku-kilkunastu) nie należy sortować quicksortem, tylko którymś z algorytmów o złożoności kwadratowej, choćby przez proste wstawianie.
Z praktycznego punktu widzenia lepiej byłoby tu zastosować opisany również w [10] algorytm Hoare'a wyznaczania mediany. Jego idea jest podobna do pomysłu sortowania quicksortem. Losuje się bowiem jedną z wartości ciągu, a następnie rozrzuca pozostałe wartości na 3 grupy: elementów mniejszych, równych i większych od tej wartości, po czym szuka się elementu o odpowiednim numerze w jednej z tych grup, tą samą zresztą metodą. Ten algorytm ma kwadratową złożoność pesymistyczną (gdy zawsze będziemy mieli pecha i wybierali element skrajny jako wartość, względem której rozrzucamy), ale średnio działa w czasie liniowym. W praktyce doskonale nadaje się do znajdowania mediany i jest dość prosty do zakodowania - własność bardzo ważna w trakcie zawodów.
Trzeci algorytm, trochę niepewny, bo nie dający dobrych rezultatów ze stuprocentową pewnością, to algorytm probabilistyczny polegający po prostu na kilkukrotnym wylosowaniu dowolnej wartości i sprawdzeniu, czy jest ona liderem. Zauważmy, że jeśli lider istnieje, to z prawdopodobieństwem większym niż 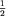 wylosujemy właśnie jego. Jeżeli na przykład po dziesięciu losowaniach nie natrafimy na lidera, to uznajemy, że lidera nie ma i dajemy odpowiedź TAK. Prawdopodobieństwo błędu jest mniejsze niż
wylosujemy właśnie jego. Jeżeli na przykład po dziesięciu losowaniach nie natrafimy na lidera, to uznajemy, że lidera nie ma i dajemy odpowiedź TAK. Prawdopodobieństwo błędu jest mniejsze niż 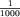 . W praktyce tego typu rozwiązania są stosowane i na olimpiadzie czasami bardzo skuteczne. Tutaj wadą jest konieczność wielokrotnego przeglądania całego ciągu wejściowego. Im większą chcemy mieć pewność, tym więcej to kosztuje. Testy były tak przygotowane, żeby z dużym prawdopodobieństwem spowodować podanie złej odpowiedzi, albo przekroczenie limitu czasowego, co najmniej w jednym z zestawów. Ale podobnie jak zawodnicy, którzy użyli tego algorytmu do rozwiązania naszego zadania, nie mogli być pewni, czy otrzymają dobre wyniki, tak i organizatorzy, sprawdzając zadanie, nie mogli być pewni, czy wychwycą niepewne rozwiązanie.
. W praktyce tego typu rozwiązania są stosowane i na olimpiadzie czasami bardzo skuteczne. Tutaj wadą jest konieczność wielokrotnego przeglądania całego ciągu wejściowego. Im większą chcemy mieć pewność, tym więcej to kosztuje. Testy były tak przygotowane, żeby z dużym prawdopodobieństwem spowodować podanie złej odpowiedzi, albo przekroczenie limitu czasowego, co najmniej w jednym z zestawów. Ale podobnie jak zawodnicy, którzy użyli tego algorytmu do rozwiązania naszego zadania, nie mogli być pewni, czy otrzymają dobre wyniki, tak i organizatorzy, sprawdzając zadanie, nie mogli być pewni, czy wychwycą niepewne rozwiązanie.
Czwarty algorytm, wzorcowy, i bardzo elegancki, którego poprawność jest wysoce nieoczywista. Algorytm ten opisany jest w książce [23]. Ze względu na prostotę algorytmu podamy tutaj jego pełny kod pascalowy.
| 1 | { Zakładamy, że elementy ciągu podane są w tablicy A[1..n]. |
| 2 | Algorytm stwierdza, czy w tablicy A znajduje się lider. } |
| 3 | ile:=1; l:=A[1]; { l - kandydat na lidera } |
| 4 | for i:=2 to n do |
| 5 | if A[i]=l then ile:=ile+1 |
| 6 | end if ile = 1 then l:=A[i] |
| 7 | end ile:=ile-1; |
| 8 | { Po tej pętli, jeśli w A jest lider, to jest on równy l. |
| 9 | Sprawdzamy więc, czy l jest liderem. } |
| 10 | ile:=0; |
| 11 | for i:=1 to n do if A[i]=l then ile:=ile+1; |
| 12 | if ile > n div 2 then { lider jest } |
| 13 | end { lidera nie ma } |
Uwaga: aby użyć tego algorytmu do rozwiązania naszego zadania, w drugiej pętli należy dodać fragment sprawdzający warunek (2) z udowodnionego twierdzenia. Fragment ten pominęliśmy, aby nie popsuć przejrzystości tekstu.
Nie od razu widać, dlaczego ten algorytm miałby dawać poprawne odpowiedzi. Najlepiej się o tym przekonać próbując skonstruować kontrprzykład. Po kilku próbach okaże się to niemożliwe. Pełny dowód poprawności algorytmu jednak nie jest banalny. Przy okazji warto zauważyć, że o ile poprzednie algorytmy potrzebowały tablicy do zapamiętania wszystkich wartości ciągu, to tutaj możemy z tablicy zrezygnować i wczytywać na bieżąco wartości z pliku. Dwukrotne wczytanie wystarcza, żeby stwierdzić istnienie lidera. Algorytm ten ma zatem koszt czasowy liniowy, a pamięciowy stały.
Pozostaje jeszcze wyjaśnić, dlaczego tor o podanych własnościach nazwaliśmy lollobrygidą. Narciarze zapewne wiedzą, że taką nazwę nosi jedna z bardzo muldziastych tras narciarskich w Szczyrku. Dlaczego jednak trasa ta została nazwana nazwiskiem słynnej włoskiej aktorki, pozostawmy dociekliwości czytelników.
Testy i czasy odcięcia zostały tak dobrane, aby możliwie jak najdokładniej oddzielić algorytmy liniowe od algorytmów o czasie działania rzędu 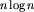 i wyeliminować programy błędne (np. zgadujące odpowiedź).
i wyeliminować programy błędne (np. zgadujące odpowiedź).
Każdy test składa się z 30 przypadków. Pierwsze 4 testy, to testy poprawnościowe, zawierające same proste przypadki (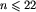 ). Następne 6 testów, to testy wydajnościowe. Zawierają po kilka przypadków dużych danych (
). Następne 6 testów, to testy wydajnościowe. Zawierają po kilka przypadków dużych danych (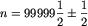 ), pozostałe przypadki są podobne co do wielkości do pierwszych czterech testów.
), pozostałe przypadki są podobne co do wielkości do pierwszych czterech testów.
Oto opisy poszczególnych testów:
 elementów się nie powtarza (tzn. nie ma "prawie lidera"), wówczas konstrukcja lollobrygidy może być dla niektórych algorytmów nieco trudniejsza.
elementów się nie powtarza (tzn. nie ma "prawie lidera"), wówczas konstrukcja lollobrygidy może być dla niektórych algorytmów nieco trudniejsza.
W testach wydajnościowych występują przemieszane wszystkie 4 powyższe przypadki parzystości i istnienia, lub nie, lidera.
Czasy odcięcia były dobrane tak, aby więcej niż dwukrotnie przewyższały czas działania wzorcowego rozwiązania, ale dla dużych testów powodowały odcięcie przy korzystaniu z procedur sortujących. Małe testy doczepione zostały do dużych aby wyeliminować algorytmy zgadujące odpowiedzi, bowiem jedynie rozwiązanie kompletu 30 przypadków zaliczało test.