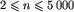 .
.Drużyna narciarska organizuje trening na Bajtogórze. Na północnym stoku góry znajduje się jeden wyciąg. Wszystkie trasy prowadzą od górnej do dolnej stacji wyciągu. W trakcie treningu członkowie drużyny będą razem startować z górnej stacji wyciągu i spotykać się przy dolnej stacji. Poza tymi dwoma punktami trasy, zawodników nie mogą się przecinać, ani stykać. Wszystkie trasy muszą cały czas prowadzić w dół.
Mapa tras narciarskich składa się z sieci polan połączonych przecinkami. Każda polana leży na innej wysokości. Dwie polany mogą być bezpośrednio połączone co najwyżej jedną przecinką. Zjeżdżając od górnej do dolnej stacji wyciągu można tak wybrać drogę, żeby odwiedzić dowolną polanę (choć być może nie wszystkie w jednym zjeździe). Trasy narciarskie mogą się przecinać tylko na polanach i nie prowadzą przez tunele, ani estakady.
Napisz program, który:
W pierwszym wierszu pliku wejściowego NAR.IN znajduje się jedna liczba całkowita n równa liczbie polan, 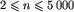 .
.
W każdym z kolejnych n-1 wierszy znajduje się ciąg liczb całkowitych pooddzielanych pojedynczymi odstępami. Liczby w (i+1)-szym wierszu pliku określają, do których polan prowadzą w dół przecinki od polany nr i. Pierwsza liczba k w wierszu określa liczbę tych polan, a kolejne k liczb to ich numery, które są uporządkowane wg ułożenia prowadzących do nich przecinek w kierunku ze wschodu na zachód. Polany są ponumerowane liczbami od 1 do n. Górna stacja wyciągu znajduje się na polanie numer 1, a dolna na polanie numer n.
W pierwszym i jedynym wierszu pliku wyjściowego NAR.OUT powinna znajdować się dokładnie jedna liczba całkowita - maksymalna liczba narciarzy mogących wziąć udział w treningu.
15 5 3 5 9 2 4 1 9 2 7 5 2 6 8 1 7 1 10 2 14 11 2 10 12 2 13 10 3 13 15 12 2 14 15 1 15 1 15 1 15poprawną odpowiedzią jest plik wyjściowy NAR.OUT
3
Zadanie to możemy sformułować w języku teorii grafów. Mamy dany acykliczny, planarny graf skierowany - wierzchołki tego grafu to polany i stacje wyciągu, a krawędzie to przecinki. W grafie tym mamy wyróżnione dwa wierzchołki reprezentujące górną i dolną stację wyciągu. Z górnej stacji wyciągu osiągalne są wszystkie wierzchołki w grafie. Podobnie, z każdego wierzchołka w grafie osiągalna jest dolna stacja wyciągu. Ponadto stacje wyciągu (jako najwyżej i najniżej położone wierzchołki) znajdują się na obwodzie grafu. Należy wyznaczyć maksymalną liczbę k takich ścieżek w grafie, które prowadzą od górnej do dolnej stacji wyciągu i poza stacjami wyciągu nie mają (parami) żadnych wspólnych wierzchołków.
Załóżmy chwilowo, że w grafie nie ma krawędzi łączącej bezpośrednio górną i dolną stację wyciągu. Jeżeli taka krawędź jest, to możemy ją usunąć, obliczyć wynik, po czym zwiększyć go o 1.
Zadanie to możemy rozwiązać za pomocą algorytmu zachłannego. Wyobraźmy sobie, że wybraliśmy k ścieżek spełniających warunki zadania. Oznaczmy te ścieżki, od lewej do prawej (ze wschodu na zachód), przez s_1, ..., s_k. Zauważmy, że bez łamania warunków zadania możemy przesunąć skrajnie lewą (wschodnią) ścieżkę s1 w lewo tak, aby prowadziła przez wierzchołki leżące na lewym pół-obwodzie grafu.
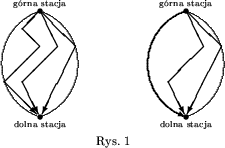
Tak więc, bez zmniejszenia ogólności, możemy przyjąć, że s1 biegnie przez wierzchołki leżące na lewym pół-obwodzie grafu (zobacz rysunek 1).
Podobnie możemy poprzesuwać pozostałe ścieżki. Zauważmy, że wśród wszystkich możliwych ścieżek, które prowadzą od górnej do dolnej stacji wyciągu i nie mają (za wyjątkiem stacji wyciągu) wspólnych wierzchołków z s1, istnieje skrajnie lewa ścieżka. Bez naruszenia warunków zadania możemy przyjąć, że s2 jest właśnie taką ścieżką. Analogicznie ustalamy kolejne ścieżki. Przyjmujemy, że si jest skrajnie lewą spośród wszystkich możliwych ścieżek, które prowadzą od górnej do dolnej stacji wyciągu i nie mają (za wyjątkiem stacji wyciągu) wspólnych wierzchołków z żadną ze ścieżek  .
.
Wyłania się następujący schemat algorytmu:
 ;
;
 ,
,
Pozostał do rozwiązania problem jak wyznaczyć skrajnie lewą ścieżkę w odpowiednim podgrafie zadanego grafu. Ścieżkę taką konstruujemy począwszy od górnej stacji wyciągu, korzystając z procedury przeszukiwania grafu w głąb (zobacz [13] lub [13]). Ważne jest, aby w trakcie przeszukiwania przeglądać krawędzie wychodzące z danego wierzchołka w kolejności od lewej do prawej (ze wschodu na zachód), czyli zgodnie z kolejnością, w jakiej zostały one podane w pliku wejściowym. W momencie osiągnięcia dolnej stacji wyciągu przerywamy przeszukiwanie - szukana ścieżka znajduje się wówczas na stosie. W trakcie przeszukiwania grafu kolorujemy odwiedzone wierzchołki. Zauważmy, że pokolorowane zostają wierzchołki tworzące skonstruowaną ścieżkę oraz niektóre wierzchołki leżące na lewo od tej ścieżki. Konstruując kolejne ścieżki omijamy wierzchołki już pokolorowane (za wyjątkiem stacji wyciągu).
Powyższy algorytm znajdowania skrajnie lewej ścieżki można zaimplementować w następujący sposób.
| 1 | const |
| 2 | MaxN = 5 000; { Maksymalna liczba polan (wierzchołków grafu) } |
| 3 | |
| 4 | type |
| 5 | { Lista sąsiedztwa jednego wierzchołka. } |
| 6 | { Element 0-wy zawiera liczbę wierzchołków na liście. } |
| 7 | TListaSasiedztwa = array [0..MaxN] of Integer; |
| 8 | PListaSasiedztwa = ^TListaSasiedztwa; |
| 9 | |
| 10 | var |
| 11 | { Graf reprezentowany jako listy sąsiedztwa wierzchołków. } |
| 12 | T: array [1..MaxN] of PListaSasiedztwa; |
| 13 | { Tablica do kolorowania odwiedzonych wierzchołków. } |
| 14 | Odwiedzony: array [1..MaxN] of Boolean; |
| 15 | N: Integer; { Liczba wierzchołków. } |
| 16 | |
| 17 | function Wglab (w: Integer): Boolean; |
| 18 | { Realizuje przeszukanie grafu T w głąb począwszy od wierzchołka w. |
| 19 | Zwraca true w przypadku dotarcia do dolnej stacji (sukcesu). } |
| 20 | var |
| 21 | i: Integer; |
| 22 | s: Boolean; |
| 23 | begin |
| 24 | if w = N then |
| 25 | { Osiągnięto dolną stację wyciągu. } |
| 26 | Wglab := true |
| 27 | end begin |
| 28 | Odwiedzony[w] := true; s := false; i := 1; |
| 29 | { Przeszukuj aż do pierwszego sukcesu. } |
| 30 | while not s and (i 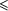 T[w]^[0]) do begin T[w]^[0]) do begin |
| 31 | if not Odwiedzony [T[w]^[i]] then |
| 32 | s := Wglab (T[w]^[i]); |
| 33 | Inc (i) |
| 34 | end; |
| 35 | Wglab := s |
| 36 | end |
| 37 | end; |
Szukaną liczbę ścieżek możemy wyznaczyć w następujący sposób:
| 1 | function ZnajdzRozwiazanie: Integer; |
| 2 | { Znajduje rozwiązanie metodą poszukiwania najbardziej |
| 3 | skrajnej ścieżki. } |
| 4 | var |
| 5 | i: Integer; |
| 6 | |
| 7 | function UsunTraseBezposrednia: Boolean; |
| 8 | { Usuwa ewentualną bezpośrednią krawędź 1 N, N, |
| 9 | zwraca true, gdy takie połączenie istniało. } |
| 10 | var |
| 11 | i, j, lnast: Integer; |
| 12 | zn: Boolean; |
| 13 | begin |
| 14 | i := 1; zn := false; lnast := T[1]^[0]; |
| 15 | while (i 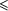 lnast) and not zn do lnast) and not zn do |
| 16 | if T[1]^[i] = N then |
| 17 | zn := true |
| 18 | end |
| 19 | Inc (i); |
| 20 | if zn then begin |
| 21 | for j := i to lnast - 1 do T[1]^[j] := T[1]^[j+1]; |
| 22 | Dec (T[1]^[0]) |
| 23 | end |
| 24 | UsunTraseBezposrednia := zn |
| 25 | end |
| 26 | |
| 27 | begin { ZnajdzRozwiazanie. } |
| 28 | for i := 1 to N do Odwiedzony [i] := false; |
| 29 | if UsunTraseBezposrednia then i := 1 end i := 0; |
| 30 | while Wglab (1) do Inc (i); |
| 31 | ZnajdzRozwiazanie := i |
| 32 | end |
Z twierdzenia Eulera wiadomo (zobacz [10]), że w każdym spójnym grafie planarnym liczba krawędzi m jest takiego rzędu jak liczba wierzchołków n. Dokładniej, dla 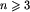 mamy
mamy 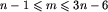 . Jeżeli więc nie będziemy alokowali w pamięci całych tablic sąsiedztwa, a jedynie ich wypełnione fragmenty, to uzyskamy złożoność pamięciową algorytmu rzędu n.
. Jeżeli więc nie będziemy alokowali w pamięci całych tablic sąsiedztwa, a jedynie ich wypełnione fragmenty, to uzyskamy złożoność pamięciową algorytmu rzędu n.
Sprawdzenie, czy w grafie jest krawędź łącząca bezpośrednio górną i dolną krawędź wyciągu wymaga przejrzenia wszystkich krawędzi wychodzących z górnej stacji wyciągu. Tak więc złożoność czasowa tej operacji jest rzędu n. Zauważmy, że w trakcie przeglądania grafu po każdej krawędzi przechodzimy co najwyżej raz. Stąd, złożoność czasowa przeszukiwania grafu jest rzędu n. Tak więc, złożoność czasowa całego rozwiązania jest rzędu n.
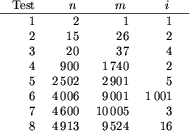
Do sprawdzenia rozwiązań zawodników użyto 8-miu testów. Testy te można podzielić na trzy grupy:
W poniższej tabelce podano wielkości i wyniki dla poszczególnych testów.