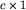 , zielone
, zielone 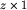 , a niebieskie
, a niebieskie 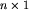 , gdzie c, z i n są liczbami naturalnymi. Gracze dysponują nieograniczoną pulą pasków każdego koloru (jeśli pewnych pasków zabraknie, to zawsze można dodrukować).
, gdzie c, z i n są liczbami naturalnymi. Gracze dysponują nieograniczoną pulą pasków każdego koloru (jeśli pewnych pasków zabraknie, to zawsze można dodrukować).Paski to gra dwuosobowa. Rekwizytami potrzebnymi do gry są paski w trzech kolorach: czerwonym, zielonym i niebieskim. Wszystkie paski czerwone mają wymiary 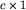 , zielone
, zielone 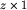 , a niebieskie
, a niebieskie 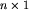 , gdzie c, z i n są liczbami naturalnymi. Gracze dysponują nieograniczoną pulą pasków każdego koloru (jeśli pewnych pasków zabraknie, to zawsze można dodrukować).
, gdzie c, z i n są liczbami naturalnymi. Gracze dysponują nieograniczoną pulą pasków każdego koloru (jeśli pewnych pasków zabraknie, to zawsze można dodrukować).
Plansza do gry jest prostokątem o wymiarach 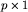 i składa się z p pól o wymiarach
i składa się z p pól o wymiarach 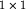 .
.
Gracze wykonują ruchy na przemian. Ruch polega na ułożeniu na planszy paska dowolnego koloru. Obowiązują przy tym następujące zasady:
Przegrywa gracz, który jako pierwszy nie może wykonać ruchu zgodnie z zasadami gry. Pierwszy gracz to gracz, który wykonuje pierwszy ruch w grze. Mówimy, że pierwszy gracz ma strategię wygrywającą, jeżeli niezależnie od posunięć drugiego gracza zawsze może wygrać.
Napisz program, który:
Pierwszy wiersz zbioru wejściowego PAS.IN zawiera trzy liczby naturalne c, z i n, 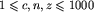 , równe długościom pasków, odpowiednio, czerwonych, zielonych i niebieskich. Liczby w wierszu są poodzielane pojedynczymi znakami odstępu.
, równe długościom pasków, odpowiednio, czerwonych, zielonych i niebieskich. Liczby w wierszu są poodzielane pojedynczymi znakami odstępu.
Drugi wiersz pliku PAS.IN zawiera jedną liczbę m, 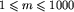 , równą liczbie różnych plansz do rozpatrzenia.
, równą liczbie różnych plansz do rozpatrzenia.
Wiersze od 3 to m+2 zawierają po jednej liczbie p, 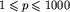 . Liczba w wierszu i+2 jest długością i-tej planszy.
. Liczba w wierszu i+2 jest długością i-tej planszy.
Plik wyjściowy PAS.OUT powinien zawierać m wierszy. W i-tym wierszu pliku powinna być zapisana jedna liczba:
1 5 1 3 1 5 6poprawną odpowiedzią jest plik wyjściowy PAS.OUT
1 1 2
W teorii gier istnieje pojęcie gry zamkniętej. Gry, które polegają na kolejnych jawnych posunięciach dwu graczy (np. gra w paski, a także szachy, warcaby, kółko i krzyżyk, wilk i owce itd.) są przykładami gier zamkniętych. Znane twierdzenie mówi, że wszystkie takie gry są niesprawiedliwe lub czcze, tzn. że zawsze albo jeden z graczy ma strategię wygrywającą, albo obaj gracze mogą co najwyżej wymusić remis lub nieskończoną rozgrywkę.
Gra w paski jest ponadto grą kategoryczną, czyli zawsze kończy się wygraną jednego z graczy. Jest zatem niesprawiedliwa: któryś z graczy musi mieć strategię prowadzącą do zwycięstwa.
Będąc młodym informatykiem, z pewnością zdajesz sobie sprawę, Szanowny Czytelniku, że teoretycznie można znajdować strategie wygrywające poprzez przeszukiwanie drzewa gry, i że chyba dla żadnej rozsądnej gry nie jest to wykonalne w praktyce. Można polemizować, czy paski są rozsądną grą, w każdym razie przeszukiwanie całego drzewa jest w tym wypadku zbyt pracochłonne.
Ruch w grze w paski można jednak postrzegać jako rozbicie planszy na mniejsze kawałki. Podsuwa nam to pomysł skorzystania z metod programowania dynamicznego. Jeśli umielibyśmy powiedzieć coś o tych "mniejszych kawałkach", to być może umielibyśmy również sklasyfikować jakoś wyjściową planszę?
Chwila namysłu pozwala stwierdzić, że nie wystarczy informacja, który z graczy ma strategię wygrywającą na każdym z kawałków planszy, by ustalić, kto ją ma na całej planszy. Potrzebujemy zatem subtelniejszego rozróżnienia pomiędzy planszami, jednak takiego, z którego łatwo wynika, kto na danej planszy zwycięży. Jakiego? O tym już za chwilę...
Szanowny Czytelniku! Być może poznałeś już program wzorcowy i wiesz, że w magiczny sposób korzysta on z właściwości operacji XOR. W tym artykule postaram się przekonać Cię, że w rozwiązaniu tym nie ma aż tak wiele magii. Użyję języka teorii grup, co w wielu miejscach uprości opis. Mimo wszystko, zajmie to jednak trochę czasu, a skoro Ty oglądałeś już rozwiązanie wzorcowe, to pewnie nie należysz do cierpliwych. Dlatego już teraz przedstawię główną myśl rozwiązania. Oto ona:
W grze w paski, jeśli w jakiejś chwili plansza daje się podzielić na dwa identyczne fragmenty, to wiadomo, że gracz, na którego przypada kolejka, musi przegrać: drugi gracz będzie powtarzał jego ruchy, tyle że symetrycznie, na drugim z identycznych fragmentów planszy. Jeśli pierwszy gracz może jeszcze wykonać ruch, to również i drugi może po nim wykonać ruch symetryczny. A jeśli pierwszy nie może, to przegrał!
Ta cecha gry w paski jest w pełni analogiczna do znanej właściwości operacji XOR, polegającej na tym, że dla dowolnej liczby k mamy 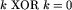 . Liczba k odpowiada jednemu z dwu identycznych egzemplarzy planszy, zaś 0 oznacza porażkę pierwszego gracza.
. Liczba k odpowiada jednemu z dwu identycznych egzemplarzy planszy, zaś 0 oznacza porażkę pierwszego gracza.
Oczywiście jest to tylko intuicja. Dlatego zachęcam nawet Ciebie, Niecierpliwy Czytelniku, do dalszej lektury.
Na początku gry plansza jest pojedynczym prostokątem zbudowanym z 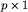 kwadratowych pól. Kolejne ruchy polegają na zakrywaniu fragmentów planszy. Pola zakryte nie biorą dalej udziału w grze. Natomiast pola wolne po każdym ruchu tworzą pewien układ spójnych prostokątów. Przykładowo, na rysunku 1 widzimy początek pewnej rozgrywki na planszy długości 24. Po pierwszym ruchu wolne pola tworzą układ dwu prostokątów o długościach 10 i 6, a po następnym mamy trzy prostokąty o długościach 3, 3 i 6.
kwadratowych pól. Kolejne ruchy polegają na zakrywaniu fragmentów planszy. Pola zakryte nie biorą dalej udziału w grze. Natomiast pola wolne po każdym ruchu tworzą pewien układ spójnych prostokątów. Przykładowo, na rysunku 1 widzimy początek pewnej rozgrywki na planszy długości 24. Po pierwszym ruchu wolne pola tworzą układ dwu prostokątów o długościach 10 i 6, a po następnym mamy trzy prostokąty o długościach 3, 3 i 6.
Definicja. Spójny prostokąt, zbudowany z wolnych pól, do którego skrajów przylegają pola zajęte lub brzegi planszy (czyli nie dający się powiększyć o kolejne wolne pola bez naruszania spójności), nazywać będziemy obszarem. Każdy układ obszarów (również początkowy, czyli zbudowany z jednego obszaru 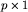 ) będziemy nazywać planszą.
) będziemy nazywać planszą.
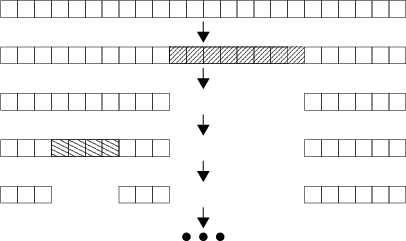
Zwróćmy uwagę, że z punktu widzenia strategii rozgrywki (w szczególności tego, kto wygra), nie ma znaczenia kolejność, w jakiej na danej planszy występują poszczególne obszary. Czyli plansze 3, 3, 6 oraz 3, 6, 3 możemy uważać za jednakowe. Dlatego odpowiednim pojęciem matematycznym do reprezentowania plansz będzie multizbiór, którego elementami będą liczby całkowite dodatnie - długości poszczególnych obszarów.
Definicja. Multizbiór jest to zbiór par (x,n), gdzie x jest elementem multizbioru, zaś n=1,2,3,... jest liczbą całkowitą dodatnią, określającą w ilu egzemplarzach dany element należy do multizbioru. Oczywiście dla każdego x do multizbioru może należeć co najwyżej jedna para postaci (x,n). Operacje sumy i części wspólnej są dla multizbiorów zdefiniowane w sposób naturalny. Na przykład, jeśli 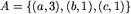 , zaś
, zaś 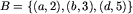 , to
, to 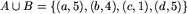 oraz
oraz 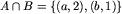 .
.
Plansze przedstawimy jako multizbiory długości tworzących je obszarów. Przykładowo, przedstawieniem planszy 3, 3, 6, jak również planszy 3, 6, 3, jest ten sam multizbiór 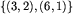 . W dalszych rozważaniach potrzebna nam będzie operacja łączenia dwu plansz, czyli budowania planszy, składającej się ze wszystkich obszarów, wchodzących w skład obu plansz. Operacji łączenia plansz dokładnie odpowiada suma multizbiorów.
. W dalszych rozważaniach potrzebna nam będzie operacja łączenia dwu plansz, czyli budowania planszy, składającej się ze wszystkich obszarów, wchodzących w skład obu plansz. Operacji łączenia plansz dokładnie odpowiada suma multizbiorów.
Rozważamy grę rozpoczynającą się od planszy 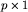 i prowadzoną przy użyciu pasków o długościach c, z i n. W każdym stanie gry plansza będzie zatem zbudowana z obszarów o długościach
i prowadzoną przy użyciu pasków o długościach c, z i n. W każdym stanie gry plansza będzie zatem zbudowana z obszarów o długościach 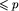 . Oczywiście, nie każda plansza zbudowana z takich obszarów może się pojawić w naszej rozgrywce, w szczególności suma długości obszarów nigdy nie przekroczy p.
. Oczywiście, nie każda plansza zbudowana z takich obszarów może się pojawić w naszej rozgrywce, w szczególności suma długości obszarów nigdy nie przekroczy p.
Na nasze potrzeby wygodnie jednak będzie o tym zapomnieć i zbadać zbiór X wszystkich plansz, zbudowanych ze skończonej liczby obszarów, z których każdy ma długość 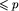 . Zatem X jest rodziną skończonych multizbiorów, których elementy są liczbami od 1 do p. Dzięki temu, w zbiorze X wykonalne jest działanie łączenia plansz (czyli dodawania multizbiorów) - to znaczy, że plansza uzyskana przez połączenie dwu elementów zbioru X również należy do tego zbioru. Zwróćmy uwagę, że w zbiorze X znajduje się również plansza pusta, czyli pusty multizbiór (odpowiada ona całkowitemu wypełnieniu planszy paskami). Oznaczmy ją przez
. Zatem X jest rodziną skończonych multizbiorów, których elementy są liczbami od 1 do p. Dzięki temu, w zbiorze X wykonalne jest działanie łączenia plansz (czyli dodawania multizbiorów) - to znaczy, że plansza uzyskana przez połączenie dwu elementów zbioru X również należy do tego zbioru. Zwróćmy uwagę, że w zbiorze X znajduje się również plansza pusta, czyli pusty multizbiór (odpowiada ona całkowitemu wypełnieniu planszy paskami). Oznaczmy ją przez  . Dla dowolnego
. Dla dowolnego 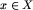 mamy oczywiście
mamy oczywiście 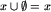 , czyli
, czyli  jest elementem neutralnym dla działania łączenia plansz. Nadto łączenie plansz jest, jak każdy widzi, przemienne i (jak sama nazwa wskazuje) łączne.
jest elementem neutralnym dla działania łączenia plansz. Nadto łączenie plansz jest, jak każdy widzi, przemienne i (jak sama nazwa wskazuje) łączne.
Definicja. Zbiór Y z działaniem dwuargumentowym + nazywamy grupą przemienną albo abelową, jeśli spełnia on następujące warunki:
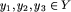 mamy y_1+(y_2+y_3)=(y_1+y_2)+y_3.
mamy y_1+(y_2+y_3)=(y_1+y_2)+y_3.
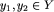 zachodzi y_1+y_2=y_2+y_1.
zachodzi y_1+y_2=y_2+y_1.
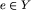 taki, że dla każdego
taki, że dla każdego 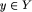 zachodzi y+e=e+y=y. Element e nazywamy elementem neutralnym grupy.
zachodzi y+e=e+y=y. Element e nazywamy elementem neutralnym grupy.
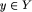 istnieje taki
istnieje taki 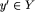 , że y+y'=e. Przyjmuje się oznaczenie -y=y'. Mówimy, że -y jest elementem odwrotnym do y.
, że y+y'=e. Przyjmuje się oznaczenie -y=y'. Mówimy, że -y jest elementem odwrotnym do y.
Pojęcie grupy przemiennej powinno być dobrze znane każdemu: najprostsze przykłady to liczby całkowite (lub wymierne, lub rzeczywiste) z dodawaniem (w tym kontekście mówi się raczej o elemencie przeciwnym, a nie odwrotnym), liczby wymierne (lub rzeczywiste) bez zera z mnożeniem, wektory na płaszczyźnie z dodawaniem wektorów, itd.
Widzimy, że zbiór X z działaniem  spełnia wszystkie warunki oprócz odwracania. Przypomnijmy sobie jednak, że na planszy, dającej się podzielić na dwa identyczne fragmenty gracz, na którego przypada kolejka, musi przegrać, tak samo jak na planszy
spełnia wszystkie warunki oprócz odwracania. Przypomnijmy sobie jednak, że na planszy, dającej się podzielić na dwa identyczne fragmenty gracz, na którego przypada kolejka, musi przegrać, tak samo jak na planszy  . Z punktu widzenia strategii można więc uważać, że plansza postaci
. Z punktu widzenia strategii można więc uważać, że plansza postaci 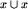 jest równoważna planszy
jest równoważna planszy  . Postaramy się zatem tak przerobić zbiór X z działaniem
. Postaramy się zatem tak przerobić zbiór X z działaniem  , by każdy jego element był odwrotny sam do siebie. Z grubsza biorąc, utożsamimy elementy postaci
, by każdy jego element był odwrotny sam do siebie. Z grubsza biorąc, utożsamimy elementy postaci 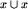 z
z  . Znów będzie nam potrzebna
. Znów będzie nam potrzebna
Definicja. Relacja dwuargumentowa  na zbiorze Y jest relacją równoważności, jeśli jest
na zbiorze Y jest relacją równoważności, jeśli jest
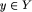 zachodzi
zachodzi 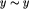 ,
,
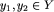 jeśli
jeśli 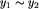 , to również
, to również 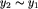 ,
,
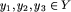 zachodzi
zachodzi 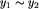 oraz
oraz 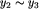 , to także
, to także 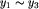 .
.
Relacje równoważności są matematycznym sposobem na utożsamienie pewnych elementów zbioru: każda relacja równoważności na zbiorze Y jednoznacznie zadaje jego podział, czyli rodzinę  podzbiorów zbioru Y taką, że
podzbiorów zbioru Y taką, że 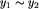 wtedy i tylko wtedy, gdy dla pewnego elementu B rodziny
wtedy i tylko wtedy, gdy dla pewnego elementu B rodziny 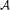 zachodzi jednocześnie
zachodzi jednocześnie 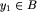 oraz
oraz 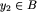 . Taką rodzinę oznacza się przez
. Taką rodzinę oznacza się przez 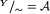 . Każdy element
. Każdy element 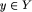 należy do dokładnie jednego elementu
należy do dokładnie jednego elementu 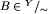 ; ten jedyny element oznaczamy [y]=B i nazywamy klasą abstrakcji elementu y. Oczywiście [y_1]=[y_2] wtedy i tylko wtedy, gdy
; ten jedyny element oznaczamy [y]=B i nazywamy klasą abstrakcji elementu y. Oczywiście [y_1]=[y_2] wtedy i tylko wtedy, gdy 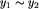 . Czyli
. Czyli ![[y]subseteq Y](img/blue259.png) jest zbiorem tych i tylko tych elementów zbioru Y, które właśnie utożsamiliśmy z y za pomocą relacji
jest zbiorem tych i tylko tych elementów zbioru Y, które właśnie utożsamiliśmy z y za pomocą relacji  .
.
Dobrym pomysłem okazuje się następujące określenie naszej relacji: 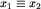 wtedy i tylko wtedy, gdy na planszy
wtedy i tylko wtedy, gdy na planszy 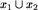 gracz rozpoczynający musi przegrać (tzn. jego przeciwnik posiada strategię wygrywającą). Wiemy zatem, że zawsze
gracz rozpoczynający musi przegrać (tzn. jego przeciwnik posiada strategię wygrywającą). Wiemy zatem, że zawsze  . Poza tym jest oczywiście wiele innych par x_1, x_2 takich, że
. Poza tym jest oczywiście wiele innych par x_1, x_2 takich, że 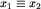 - jak się niedługo okaże, działa to na naszą korzyść. Przypominam, że rozmiary pasków c, z, n są cały czas ustalone. Dla innych rozmiarów pasków możemy otrzymać zupełnie inną relację!
- jak się niedługo okaże, działa to na naszą korzyść. Przypominam, że rozmiary pasków c, z, n są cały czas ustalone. Dla innych rozmiarów pasków możemy otrzymać zupełnie inną relację!
Z drugiej strony, uważny Czytelnik niedługo już zorientuje się, że utożsamianie plansz, na których gracz rozpoczynający ma strategię wygrywającą, byłoby dużo gorszym pomysłem. Poza bardzo prostymi przypadkami, musielibyśmy wówczas w trosce o przechodniość naszej relacji konsekwentnie posklejać ze sobą wszystko.
Zadanie dla czytelnika. Proszę sprawdzić, że  jest istotnie relacją równoważności (spełnia definicję). Wskazówka: aby udowodnić przechodniość, należy, znając strategię wygrywającą drugiego gracza dla plansz
jest istotnie relacją równoważności (spełnia definicję). Wskazówka: aby udowodnić przechodniość, należy, znając strategię wygrywającą drugiego gracza dla plansz 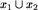 oraz
oraz 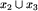 , opisać sposób (algorytm) gry dla drugiego gracza, który zagwarantuje mu zwycięstwo na planszy
, opisać sposób (algorytm) gry dla drugiego gracza, który zagwarantuje mu zwycięstwo na planszy 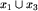 .
.
Zagadka tylko dla wtajemniczonych: czy jeśli zdefiniowalibyśmy  jako najmniejszą relację równoważności na X, która utożsamia wszystkie plansze postaci
jako najmniejszą relację równoważności na X, która utożsamia wszystkie plansze postaci 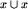 z
z  , to czy
, to czy  ? A gdyby dodatkowo zarządać, by
? A gdyby dodatkowo zarządać, by  było najmniejszą kongruencją na X ze względu na
było najmniejszą kongruencją na X ze względu na  ?
?
No dobrze, powiecie, utożsamiliśmy jakieś elementy, ale przecież działanie  było określone na X, a my mamy teraz inny zbiór
było określone na X, a my mamy teraz inny zbiór 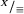 . A jednak wszystko jest pod kontrolą! Przypomnijmy tylko jedno pojęcie, z którym każdy spotkał się (lub spotka) w szkole:
. A jednak wszystko jest pod kontrolą! Przypomnijmy tylko jedno pojęcie, z którym każdy spotkał się (lub spotka) w szkole:
Definicja. Relacja równoważności  jest kongruencją na zbiorze Y ze względu na działanie +, jeśli dla dowolnych
jest kongruencją na zbiorze Y ze względu na działanie +, jeśli dla dowolnych 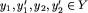 jeśli tylko
jeśli tylko 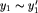 oraz
oraz 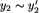 , to zachodzi również
, to zachodzi również 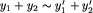 .
.
Przypadek "szkolny" to relacja przystawania modulo n, która utożsamia liczby całkowite 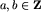 wtedy i tylko wtedy, gdy a-b dzieli się przez n. Jest to relacja równoważności, co więcej jest to kongruencja ze względu na dodawanie, odejmowanie i mnożenie.
wtedy i tylko wtedy, gdy a-b dzieli się przez n. Jest to relacja równoważności, co więcej jest to kongruencja ze względu na dodawanie, odejmowanie i mnożenie.
Kongruencja pozwala wykonywać działania w zbiorze klas abstrakcji 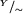 : aby np. dodać dwie klasy, bierzemy dowolną parę ich elementów i dodajemy, a następnie znajdujemy klasę abstrakcji sumy. To, że relacja jest kongruencją, nie oznacza nic więcej, niż że tak zdefiniowane działanie jest dobrze określone w zbiorze
: aby np. dodać dwie klasy, bierzemy dowolną parę ich elementów i dodajemy, a następnie znajdujemy klasę abstrakcji sumy. To, że relacja jest kongruencją, nie oznacza nic więcej, niż że tak zdefiniowane działanie jest dobrze określone w zbiorze 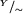 , tzn. że różne wybory reprezentantów prowadzą w wyniku do tej samej klasy abstrakcji.
, tzn. że różne wybory reprezentantów prowadzą w wyniku do tej samej klasy abstrakcji.
Na całe szczęście,  jest kongruencją w X ze względu na
jest kongruencją w X ze względu na  . Proszę to sprawdzić wprost z definicji, dowód będzie podobny do dowodu faktu, że relacja
. Proszę to sprawdzić wprost z definicji, dowód będzie podobny do dowodu faktu, że relacja  jest przechodnia.
jest przechodnia.
Mamy zatem
Fakt. 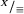 z działaniem zadanym przez
z działaniem zadanym przez  jest grupą przemienną, z elementem neutralnym
jest grupą przemienną, z elementem neutralnym ![[emptyset]](img/blue276.png) (klasa abstrakcji zbioru pustego). Działanie w tej grupie również będziemy oznaczać
(klasa abstrakcji zbioru pustego). Działanie w tej grupie również będziemy oznaczać  , zaś element neutralny po prostu przez
, zaś element neutralny po prostu przez ![0=[emptyset]](img/blue277.png) .
.
Istotnie, podzielenie X przez  nie mogło popsuć łączności, ani przemienności
nie mogło popsuć łączności, ani przemienności  , ani neutralności
, ani neutralności  (która przeniosła się na całą klasę abstrakcji
(która przeniosła się na całą klasę abstrakcji ![[emptyset]](img/blue276.png) ), i oczywiście uzyskaliśmy elementy odwrotne: każdy element jest odwrotny sam do siebie.
), i oczywiście uzyskaliśmy elementy odwrotne: każdy element jest odwrotny sam do siebie.
Potrzeba wyjaśnić, czemu miał służyć ten długi ciąg definicji. Celów było kilka. Po pierwsze, możemy teraz zwięźle sformułować nasz cel: algorytm ma stwierdzać, czy dla danej planszy x, składającej się z jednego obszaru długości p, zachodzi 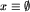 , czyli czy [x]=0 (gdyż zgodnie z naszą definicją,
, czyli czy [x]=0 (gdyż zgodnie z naszą definicją, 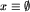 wtedy i tylko wtedy, gdy drugi gracz ma strategię wygrywającą na planszy
wtedy i tylko wtedy, gdy drugi gracz ma strategię wygrywającą na planszy 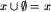 ).
).
Po drugie, bez określenia naszej grupy 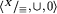 wiele faktów, które w tej chwili są dla nas najzupełniej oczywiste, należałoby za każdym razem dowodzić "ręcznie" w sposób podobny do dowodu przechodniości relacji
wiele faktów, które w tej chwili są dla nas najzupełniej oczywiste, należałoby za każdym razem dowodzić "ręcznie" w sposób podobny do dowodu przechodniości relacji  (a więc byłyby one pozostawione jako zadania dla Ciebie, Szanowny Czytelniku). Przykład takiego faktu: jeśli na planszy x strategię wygrywającą ma drugi gracz (w szczególności, jeśli np.
(a więc byłyby one pozostawione jako zadania dla Ciebie, Szanowny Czytelniku). Przykład takiego faktu: jeśli na planszy x strategię wygrywającą ma drugi gracz (w szczególności, jeśli np. 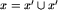 ), to na planszy
), to na planszy 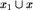 strategię wygrywającą ma ten sam gracz, co na planszy x1. Uzasadnienie: [x]=0, więc
strategię wygrywającą ma ten sam gracz, co na planszy x1. Uzasadnienie: [x]=0, więc ![[x_1]cup[x]=[x_1]](img/blue283.png) . Własności grup pozwalają nam wycisnąć wszystko co się da z przeprowadzonych już przez Ciebie dowodów, że
. Własności grup pozwalają nam wycisnąć wszystko co się da z przeprowadzonych już przez Ciebie dowodów, że  jest relacją równoważności i kongruencją ze względu na
jest relacją równoważności i kongruencją ze względu na  .
.
Po trzecie i najważniejsze, jak się za chwilę okaże, klasy abstrakcji naszej relacji dają się efektywnie obliczać metodą programowania dynamicznego.
Na drodze do rozwiązania czeka nas jeszcze jedno niespodziewane odkrycie: klasy plansz (czyli klasy abstrakcji relacji  ) dają się uporządkować!
) dają się uporządkować!
Zauważmy najpierw, że dla dowolnej planszy x, jeśli ![[x]not=0](img/blue284.png) , to z planszy x można jednym ruchem dojść do pewnej planszy
, to z planszy x można jednym ruchem dojść do pewnej planszy ![x_0in0=[emptyset]](img/blue285.png) . Innymi słowy, z każdej planszy x wygrywającej dla gracza, na którego przypada kolejka, można zawsze jednym ruchem przejść do jakiejś planszy x0 przegrywającej dla gracza, którego kolejka wypadnie po tym ruchu (a więc który będzie musiał położyć pierwszy pasek na planszy x0). Jest to ten właśnie ruch, który graczowi rozpoczynającemu grę na planszy x gwarantuje zwycięstwo. Oczywiście, na planszy x być może da się wykonać wiele innych ruchów, które mogą prowadzić do plansz z innych klas. Ważne jest jednak istnienie co najmniej jednego wygrywającego posunięcia dla każdej spośród plansz z klasy
. Innymi słowy, z każdej planszy x wygrywającej dla gracza, na którego przypada kolejka, można zawsze jednym ruchem przejść do jakiejś planszy x0 przegrywającej dla gracza, którego kolejka wypadnie po tym ruchu (a więc który będzie musiał położyć pierwszy pasek na planszy x0). Jest to ten właśnie ruch, który graczowi rozpoczynającemu grę na planszy x gwarantuje zwycięstwo. Oczywiście, na planszy x być może da się wykonać wiele innych ruchów, które mogą prowadzić do plansz z innych klas. Ważne jest jednak istnienie co najmniej jednego wygrywającego posunięcia dla każdej spośród plansz z klasy ![[x]not=0](img/blue284.png) .
.
Wykorzystajmy konsekwentnie tę obserwację i określmy relację dwuargumentową  na zbiorze
na zbiorze 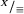 jak następuje: dla klas
jak następuje: dla klas 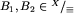 zachodzi
zachodzi 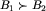 wtedy i tylko wtedy, gdy z każdej planszy
wtedy i tylko wtedy, gdy z każdej planszy 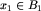 można jednym ruchem dojść do pewnej planszy
można jednym ruchem dojść do pewnej planszy 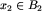 .
.
Na razie wiemy tylko, że dla ![[x]=Bnot=0](img/blue291.png) jest
jest 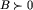 . Nie wiemy ani czy może zajść
. Nie wiemy ani czy może zajść 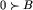 dla jakiegoś B, ani czy może być
dla jakiegoś B, ani czy może być 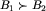 dla jakichkolwiek
dla jakichkolwiek 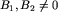 .
.
Fakt 1. (najważniejszy) Jeśli 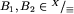 i
i 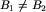 , to albo
, to albo 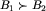 , albo
, albo 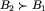 .
.
Dowód. Niech nie zachodzi ani 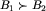 , ani
, ani 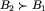 . Czyli istnieje plansza
. Czyli istnieje plansza 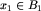 , z której jednym ruchem nie da się dojść do żadnej spośród plansz z klasy B2. Analogicznie, istnieje pewna plansza
, z której jednym ruchem nie da się dojść do żadnej spośród plansz z klasy B2. Analogicznie, istnieje pewna plansza 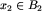 , na której żadne posunięcie nie prowadzi do klasy B1. Rozważmy planszę
, na której żadne posunięcie nie prowadzi do klasy B1. Rozważmy planszę 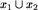 . Jeśli gracz, na którego przypada kolejność, wykona na tej połączonej planszy ruch w obrębie części x1, to przejdzie do pewnej planszy
. Jeśli gracz, na którego przypada kolejność, wykona na tej połączonej planszy ruch w obrębie części x1, to przejdzie do pewnej planszy 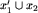 , gdzie
, gdzie 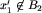 . A zatem
. A zatem ![[x'_1]not=[x_2]](img/blue300.png) . Do tej nierówności dodajmy stronami [x_2], otrzymamy
. Do tej nierówności dodajmy stronami [x_2], otrzymamy ![[x'_1]cup[x_2]not=[x_2]cup[x_2...](img/blue301.png) , czyli
, czyli ![[x'_1cup x_2]not=0](img/blue302.png) . Jest to zatem ruch prowadzący do porażki. Gracz przegra również, jeśli położy pasek w obrębie planszy x2. Czyli plansza
. Jest to zatem ruch prowadzący do porażki. Gracz przegra również, jeśli położy pasek w obrębie planszy x2. Czyli plansza 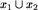 jest dla niego przegrywająca, to znaczy
jest dla niego przegrywająca, to znaczy ![[x_1cup x_2]=0](img/blue303.png) , skąd B_1=B_2, co kończy dowód.
, skąd B_1=B_2, co kończy dowód.
Fakt 2. Dla żadnego 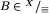 nie zachodzi
nie zachodzi 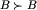 .
.
Dowód. Jeśli by tak było, to startując od dowolnej planszy 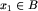 moglibyśmy wykonać ruch, prowadzący do pewnej planszy
moglibyśmy wykonać ruch, prowadzący do pewnej planszy 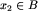 , następnie jednym ruchem przeszlibyśmy do planszy
, następnie jednym ruchem przeszlibyśmy do planszy 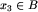 i tak w nieskończoność. A nie jest to możliwe, bo po każdym ruchu liczba wolnych pól zmniejsza się co najmniej o długość najkrótszego z pasków c, z, n!
i tak w nieskończoność. A nie jest to możliwe, bo po każdym ruchu liczba wolnych pól zmniejsza się co najmniej o długość najkrótszego z pasków c, z, n!
Fakt 3. Dla żadnych 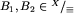 nie zachodzi jednocześnie
nie zachodzi jednocześnie 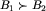 i
i 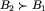 .
.
Dowód. Podobnie jak poprzednio, prowadziłoby to do istnienia nieskończonej rozgrywki, w której na zmianę przechodzilibyśmy z planszy z klasy B1 do planszy z klasy B2 i z powrotem.
Fakt 4. Jeśli 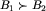 oraz
oraz 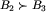 , to
, to 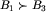 .
.
Dowód. Ten fakt jest chyba dość zaskakujący, gdyż oznacza, że z planszy z klasy B1 do planszy z klasy B3 można zawsze przejść jednym ruchem, a nie dwoma (choć oczywiście dwoma też się da). Uzasadnienie jest jednak proste: nie może oczywiście być B_1=B_3 (wykluczyliśmy to przed chwilą). Musi być zatem 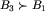 lub
lub 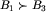 . Jednak w tym pierwszym przypadku znów znaleźlibyśmy nieskończoną rozgrywkę, prowadzącą kolejno z klasy B1 do B2, z B2 do B3, a z B3 na powrót do B1 i tak w kółko. Pozostaje jedyna możliwość
. Jednak w tym pierwszym przypadku znów znaleźlibyśmy nieskończoną rozgrywkę, prowadzącą kolejno z klasy B1 do B2, z B2 do B3, a z B3 na powrót do B1 i tak w kółko. Pozostaje jedyna możliwość 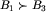 .
.
Fakt 5. Klas plansz w X jest skończenie wiele.
Dowód. (Pamiętamy, że sam zbiór X był nieskończony.) Niech xm oznacza planszę, zbudowaną z jednego obszaru długości m (czyli 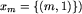 , gdzie
, gdzie 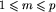 . Wówczas oczywiście każda plansza
. Wówczas oczywiście każda plansza 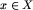 daje się przedstawić jako suma
daje się przedstawić jako suma
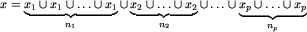
 , trzeba tylko pominąć te pary (k, n_k), dla których n_k=0.
, trzeba tylko pominąć te pary (k, n_k), dla których n_k=0.
Aby znaleźć klasę planszy x zauważmy, że ![underbrace[x_m]cup ldotscup [...](img/blue316.png) jest równe [x_m] dla nm nieparzystego, zaś 0 dla nm parzystego. Suma ta upraszcza się zatem do co najwyżej jednego składnika. W związku z tym, mamy
jest równe [x_m] dla nm nieparzystego, zaś 0 dla nm parzystego. Suma ta upraszcza się zatem do co najwyżej jednego składnika. W związku z tym, mamy
![[x]=B_1cup B_2cupldotscup B_p](img/blue317.png)
Zwróćmy uwagę, że klas plansz może nie być dokładnie 2p, tylko mniej, gdyż może się np. zdarzyć, że dla pewnych 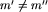 jest
jest ![[x_m']=[x_m](img/blue319.png) . Np. jeśli
. Np. jeśli 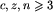 , to oczywiście 0=[x_1]=[x_2].
, to oczywiście 0=[x_1]=[x_2].
Wniosek z faktów 1-5: Klasy plansz można ponumerować kolejnymi liczbami naturalnymi tak, by klasa 0 miała numer 0 i by dla dowolnych dwóch klas B',B" numer klasy B' był większy od numeru klasy B" wtedy i tylko wtedy, gdy 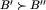 .
.
Na podstawie udowodnionych faktów wniosek ten powinien wydawać się oczywisty. Takie własności może po prostu mieć tylko naturalny porządek na liczbach naturalnych 0<1<2...<l-1<l. Jako zadanie proponuję uważnie uzasadnić ten wniosek np. przez indukcję lub posiłkując się pojęciami "dagu" (acyklicznego grafu skierowanego) i sortowania topologicznego. Klasę o numerze j będziemy od teraz oznaczać Bj. W szczególności, 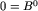 .
.
Najwyższa pora przejść do opisu algorytmu. Przypominam, że naszym celem jest obliczanie klas poszczególnych plansz.
Na podstawie wyciągniętego przed chwilą wniosku wiemy, że z każdej planszy z klasy Bj można jednym ruchem przejść do każdej z klas 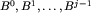 .
.
Wiemy też, że nie zachodzi 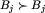 , czyli z pewnej planszy z klasy Bj nie da się wykonać ruchu tak, by pozostać w klasie Bj. Prawdą jest jednak mocniejsze stwierdzenie: nigdy nie da się wykonać ruchu tak, by pozostać w tej samej klasie. Dowód jest bardzo prosty: gdyby tak było dla pewnej planszy
, czyli z pewnej planszy z klasy Bj nie da się wykonać ruchu tak, by pozostać w klasie Bj. Prawdą jest jednak mocniejsze stwierdzenie: nigdy nie da się wykonać ruchu tak, by pozostać w tej samej klasie. Dowód jest bardzo prosty: gdyby tak było dla pewnej planszy 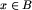 , to na planszy
, to na planszy 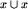 gracz pierwszy wykonałby to posunięcie na jednej z połówek, doprowadzając do sytuacji
gracz pierwszy wykonałby to posunięcie na jednej z połówek, doprowadzając do sytuacji 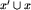 , gdzie
, gdzie 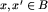 , czyli [x]=[x']=B, skąd
, czyli [x]=[x']=B, skąd ![[x'cup x]=0](img/blue328.png) . Z sytuacji dla siebie przegrywającej
. Z sytuacji dla siebie przegrywającej 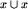 przeszedłby zatem do sytuacji, w której przegrać musi jego oponent, co oczywiście jest sprzeczne z naszymi definicjami i ze zdrowym rozsądkiem.
przeszedłby zatem do sytuacji, w której przegrać musi jego oponent, co oczywiście jest sprzeczne z naszymi definicjami i ze zdrowym rozsądkiem.
Widzimy zatem co następuje: numer planszy x to jedyna taka liczba j, że z planszy x da się jednym posunięciem przejść do każdej z klas 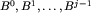 , i nie da się żadnym posunięciem przejść do żadnej spośród plansz, należących do klasy Bj.
, i nie da się żadnym posunięciem przejść do żadnej spośród plansz, należących do klasy Bj.
Ta obserwacja poprowadzi nas już prosto do algorytmu, który indukcyjnie wyznacza numery klas plansz. Dla porządku przytoczę jeszcze tylko jedną definicję:
Definicja. Jeśli Y z działaniem + jest grupą, a 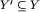 takim podzbiorem, który również jest grupą ze względu na to samo działanie, to mówimy, że Y' jest podgrupą Y.
takim podzbiorem, który również jest grupą ze względu na to samo działanie, to mówimy, że Y' jest podgrupą Y.
Przykładowo, liczby całkowite podzielne przez 3 stanowią podgrupę grupy liczb całkowitych z dodawaniem.
Oznaczmy przez  zbiór wszystkich plansz, zbudowanych z obszarów, z których żaden nie jest dłuższy niż m. Oczywiście X=X_p.
zbiór wszystkich plansz, zbudowanych z obszarów, z których żaden nie jest dłuższy niż m. Oczywiście X=X_p.
Niech 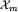 oznacza zbiór tych wszystkich klas plansz (elementów grupy
oznacza zbiór tych wszystkich klas plansz (elementów grupy 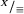 ), które mają reprezentanta z Xm. Jest on zamknięty ze względu na działanie
), które mają reprezentanta z Xm. Jest on zamknięty ze względu na działanie  i oczywiście jest podgrupą grupy
i oczywiście jest podgrupą grupy 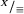 . Mamy zatem
. Mamy zatem 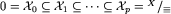 . Zauważmy też, że każdy ze zbiorów
. Zauważmy też, że każdy ze zbiorów 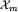 składa się z klas o kolejnych numerach, od B0 do pewnego BN. Jest tak, gdyż jeśli N jest największą liczbą taką, że
składa się z klas o kolejnych numerach, od B0 do pewnego BN. Jest tak, gdyż jeśli N jest największą liczbą taką, że 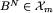 , to pewna plansza
, to pewna plansza 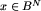 składa się z obszarów nie dłuższych niż m. Można z niej jednym ruchem dojść do każdej z klas
składa się z obszarów nie dłuższych niż m. Można z niej jednym ruchem dojść do każdej z klas  , a ruch w grze w paski nie może spowodować, by którykolwiek z obszarów wydłużył się. To dowodzi, że każda z tych klas ma reprezentanta w Xm, czyli należy do
, a ruch w grze w paski nie może spowodować, by którykolwiek z obszarów wydłużył się. To dowodzi, że każda z tych klas ma reprezentanta w Xm, czyli należy do 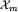 .
.
Podam teraz algorytm, który po każdym kroku dla kolejnych liczb m potrafi
 w grupie
w grupie 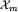 (to znaczy, wyznaczać numer klasy
(to znaczy, wyznaczać numer klasy 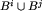 dla
dla 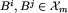 )
)
Pierwszy krok algorytmu jest trywialny: wiemy, że plansza pusta ma numer 0, a grupa 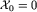 jest grupą trywialną.
jest grupą trywialną.
Załóżmy więc, że potrafimy wyznaczać klasy dla plansz z 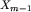 oraz że dla takich klas potrafimy wykonywać działanie
oraz że dla takich klas potrafimy wykonywać działanie  . Weźmy planszę xm zbudowaną z jednego obszaru długości m. Przejrzyjmy wszystkie możliwe ruchy, jakie możemy wykonać na tej planszy. Każdy z tych ruchów prowadzi do planszy zbudowanej z 1 lub 2 obszarów, z których każdy ma długość
. Weźmy planszę xm zbudowaną z jednego obszaru długości m. Przejrzyjmy wszystkie możliwe ruchy, jakie możemy wykonać na tej planszy. Każdy z tych ruchów prowadzi do planszy zbudowanej z 1 lub 2 obszarów, z których każdy ma długość 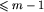 . Zatem zgodnie z założeniem potrafimy wyznaczyć numery klas wszystkich tych plansz (jeśli jakiś ruch rozspaja naszą planszę, to numer klasy wyznaczymy, obliczając
. Zatem zgodnie z założeniem potrafimy wyznaczyć numery klas wszystkich tych plansz (jeśli jakiś ruch rozspaja naszą planszę, to numer klasy wyznaczymy, obliczając  klas obu obszarów, na które rozpadła się nasza plansza). Mamy wówczas pewność, że klasa, do której należy xm, jest najmniejszą liczbą naturalną, jaka nie pojawiła się wśród otrzymanych numerów klas plansz. Jeśli np. możliwe ruchy prowadzą z xm do plansz z klas o numerach 0,1,2,3,6,9,13, to znaczy, że
klas obu obszarów, na które rozpadła się nasza plansza). Mamy wówczas pewność, że klasa, do której należy xm, jest najmniejszą liczbą naturalną, jaka nie pojawiła się wśród otrzymanych numerów klas plansz. Jeśli np. możliwe ruchy prowadzą z xm do plansz z klas o numerach 0,1,2,3,6,9,13, to znaczy, że ![[x_m]=B^4](img/blue341.png) .
.
Są tu dwie możliwości. Albo ![[x_m]in cal X_m-1](img/blue342.png) , skąd wynika, że
, skąd wynika, że 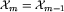 i nic więcej w tym kroku algorytmu nie musimy robić, albo z planszy xm można dojść do każdej z klas, należących do
i nic więcej w tym kroku algorytmu nie musimy robić, albo z planszy xm można dojść do każdej z klas, należących do 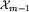 , czyli klasa [x_m] nie jest nam jeszcze znana. Ten drugi przypadek musimy rozważyć dokładniej.
, czyli klasa [x_m] nie jest nam jeszcze znana. Ten drugi przypadek musimy rozważyć dokładniej.
Wiemy, że 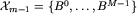 dla pewnego M. Stąd natychmiastowy wniosek, że
dla pewnego M. Stąd natychmiastowy wniosek, że ![[x_m]=B^M in cal X_msetmin...](img/blue346.png) .
.
Rozważmy teraz klasy postaci ![[x_m]cup B^j](img/blue347.png) , gdzie
, gdzie 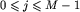 .
.
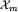 .
. 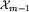 , gdyż jeśli
, gdyż jeśli ![[x_m]cup B^j=B^kin cal X_m-...](img/blue349.png) , to oczywiście mielibyśmy również
, to oczywiście mielibyśmy również ![[x_m]=[x_m]cup B^jcup B^j=B^kc...](img/blue350.png) (suma elementów Bj i Bk grupy
(suma elementów Bj i Bk grupy 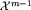 również należy do tej grupy).
również należy do tej grupy). 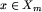 , jeśli nie należy do grupy
, jeśli nie należy do grupy 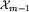 , to może być przedstawiona w tej postaci. Plansza
, to może być przedstawiona w tej postaci. Plansza 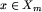 jest bowiem połączeniem pewnej (parzystej bądź nieparzystej) liczby obszarów długości m oraz planszy, należącej do
jest bowiem połączeniem pewnej (parzystej bądź nieparzystej) liczby obszarów długości m oraz planszy, należącej do 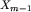 , czyli
, czyli 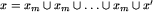 , gdzie
, gdzie 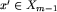 . Stąd istotnie
. Stąd istotnie ![[x]=[x_m]cup[x']](img/blue355.png) lub
lub ![[x]=[x']in cal X_m-1](img/blue356.png) , gdzie
, gdzie ![[x']=B^j](img/blue357.png) dla pewnego j< M.
dla pewnego j< M. ![[x_m]cup B^j](img/blue347.png) są między sobą różne, bo do nierówności
są między sobą różne, bo do nierówności 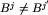 można stronami dodać [x_m].
można stronami dodać [x_m].
W takim razie mamy
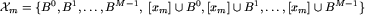
Co więcej, skoro umieliśmy wykonywać działanie  w grupie
w grupie 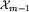 , to pamiętając, że
, to pamiętając, że ![[x_m]cup [x_m]=0](img/blue360.png) , umiemy je wykonać także w
, umiemy je wykonać także w 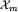 !
!
Teraz już nietrudno zgadnąć, że numerem klasy ![[x_m]cup B^j](img/blue347.png) będzie M+j. Aby się o tym przekonać, wybierzmy dowolnego reprezentanta
będzie M+j. Aby się o tym przekonać, wybierzmy dowolnego reprezentanta 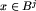 i rozważmy planszę
i rozważmy planszę 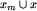 . Na tej planszy możemy wykonać ruch albo w obrębie części xm, albo x.
. Na tej planszy możemy wykonać ruch albo w obrębie części xm, albo x.
Wykonując ruch w części x możemy przejść do dowolnie wybranej spośród klas ![[x_m]cup B^i](img/blue363.png) , gdzie
, gdzie 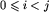 . Być może uda nam się również przejść do którejś z klas
. Być może uda nam się również przejść do którejś z klas ![[x_m]cup B^k](img/blue365.png) dla k>j, ale dla każdego takiego k znajdziemy reprezentanta
dla k>j, ale dla każdego takiego k znajdziemy reprezentanta 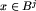 , dla którego nie będzie to możliwe. Wszystko odbywa się analogicznie jak na samej planszy
, dla którego nie będzie to możliwe. Wszystko odbywa się analogicznie jak na samej planszy 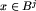 , bez dołączonej części xm.
, bez dołączonej części xm.
Natomiast kładąc pasek w części xm, możemy przejść do dowolnej klasy 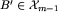 . Wystarczy wziąć
. Wystarczy wziąć 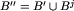 . Wiemy, że
. Wiemy, że 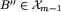 , więc istnieje taki ruch na planszy xm, który prowadzi do klasy B". Wykonując ten ruch na planszy
, więc istnieje taki ruch na planszy xm, który prowadzi do klasy B". Wykonując ten ruch na planszy 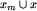 , istotnie otrzymamy w wyniku planszę klasy
, istotnie otrzymamy w wyniku planszę klasy 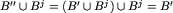 . Widzimy też, że ruch w obrębie xm nie doprowadzi nas do żadnej klasy spoza
. Widzimy też, że ruch w obrębie xm nie doprowadzi nas do żadnej klasy spoza 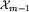 .
.
Podsumowując, widzimy wyraźnie, że:
![B^M-1prec [x_m]=[x_m]cup B^0...](img/blue370.png) .
.
Ponieważ wiemy skądinąd, że 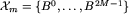 , to musi rzeczywiście zachodzić
, to musi rzeczywiście zachodzić ![[x_m]cup B^j=B^M+j](img/blue372.png) , dla każdego
, dla każdego 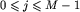 .
.
W ten sposób z nawiązką wypełniamy wszystkie warunki indukcyjne, dotyczące naszego algorytmu.
Pozostaje jeszcze jeden drobiazg: widzimy, że po pierwszym kroku znamy tylko jedną planszę (pustą), a po każdym następnym liczba znanych nam plansz (tzn. liczba elementów grupy 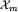 ) albo nie zmienia się, albo się podwaja. Będzie zatem zawsze potęgą dwójki. W szczególności, w całym powyższym rozumowaniu M było potęgą dwójki. Po tej uwadze nie powinno być dla Czytelnika najmniejszym problemem udowodnienie przez indukcję, że działaniu
) albo nie zmienia się, albo się podwaja. Będzie zatem zawsze potęgą dwójki. W szczególności, w całym powyższym rozumowaniu M było potęgą dwójki. Po tej uwadze nie powinno być dla Czytelnika najmniejszym problemem udowodnienie przez indukcję, że działaniu  w grupie klas plansz odpowiada dokładnie operacja XOR na numerach tych klas.
w grupie klas plansz odpowiada dokładnie operacja XOR na numerach tych klas.
W ten sposób wszystkie tajemnice gry w paski zostały ujawnione.
Na potrzeby testowania rozwiązań przygotowano 15 testów. Każdy z nich zawierał p przypadków plansz do rozpatrzenia - było to zawsze kolejno p plansz o długościach od 1 do p.
W poniższej tabeli zestawiono wartości c, z, n oraz p dla poszczególnych testów. Ponadto, k oznacza największą liczbę taką, że co najmniej jedna z plansz xm przy 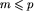 należy do klasy Bk. Dalej, W1 oznacza liczbę tych plansz spośród x_1,...,x_p, które są wygrywające dla gracza rozpoczynającego (czyli należą do klasy Bj dla j>0), zaś W2 - liczbę plansz przegrywających dla rozpoczynającego.
należy do klasy Bk. Dalej, W1 oznacza liczbę tych plansz spośród x_1,...,x_p, które są wygrywające dla gracza rozpoczynającego (czyli należą do klasy Bj dla j>0), zaś W2 - liczbę plansz przegrywających dla rozpoczynającego.
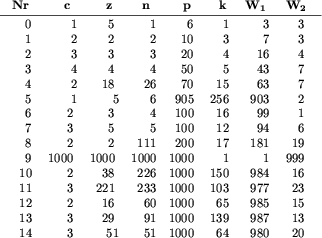
Testy 4 i 5 oraz 6, 7, 8 i 9 zostały zgrupowane.
Zadanie "Paski" było prawdopodobnie jednym z najtrudniejszych zadań w historii Olimpiady. Mimo że było zadaniem z pierwszego etapu, a więc można było poświęcić na nie wiele czasu i posiłkować się przy pracy literaturą, to jednak poprawnie rozwiązał je tylko jeden zawodnik.
Przedstawione w niniejszym artykule rozumowanie jest oparte na dowodzie poprawności programu wzorcowego. Autorem tego programu i dowodu jest Tomasz Waleń.
Podstawowe pojęcia teorii gier są przystępnie objaśnione w pierwszym rozdziale znakomitej książki [HS]. Serdecznie zachęcam do lektury!
Czytelnikom zainteresowanym tematem polecam również pozycję [JC], a w szczególności zawarte tam informacje o grze Nim. Gra ta okazuje się mieć wiele wspólnego z grą w paski. W niej także do znalezienia strategii wygrywającej przydaje się operacja XOR.
[HS] Hugo Steinhaus "Kalejdoskop matematyczny", WSiP Warszawa 1989
[JC] John Conway "On Numbers and Games", Academic Press, Inc. New York 1976