Podpisy

W Urzędzie Ochrony Bajtocji (UOB) zatrudnieni są urzędnicy oraz dowódcy. W archiwum znajdują się teczki z aktami wszystkich urzędników. W każdej teczce znajduje się podpis urzędnika oraz podpisy pracowników (urzędników lub dowódców), którzy poręczają za jego lojalność. Każdy nowoprzyjmowany urzędnik musi uzyskać przynajmniej jedno poręczenie. Z biegiem czasu lista poręczycieli może się powiększać. UOB dowiedział się ostatnio, że do grona dowódców przeniknął szpieg wrogiej Mikromięklandii. Kolejni szpiedzy byli wprowadzani do UOB na stanowiska urzędnicze dzięki poręczeniu szpiega-dowódcy i/lub innych wprowadzonych szpiegów. Tacy szpiedzy mają poręczenia wyłącznie od pracowników będących szpiegami.

Wiarygodność urzędnika można podważyć, jeżeli pośrednio nie ma on poręczenia żadnego dowódcy, który nie jest szpiegiem, tzn. nie istnieje taki ciąg pracowników UOB p_1, p_2, ..., p_k, że p₁ jest dowódcą nie będącym szpiegiem, p_k jest danym urzędnikiem i (dla i = 1, ..., k-1) p_i poręczył za .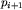

Jeżeli założenie o pewnym dowódcy, że jest szpiegiem spowodowałoby, że wiarygodność urzędnika zostałaby podważona, to urzędnik ten jest podejrzany o szpiegostwo. Dowództwo UOB chciałoby zobaczyć listę takich urzędników, i to jak najszybciej!

Przykład

Dowódcy: Anna, Grzegorz.

Urzędnicy: Bolesław (poręczyła Anna), Celina (poręczył Bolesław), Dorota (poręczyli Bolesław i Celina), Eugeniusz (poręczyli Anna i Grzegorz), Felicja (poręczył Eugeniusz), Halina (poręczyli Grzegorz i Ireneusz), Ireneusz (poręczyli Grzegorz i Halina).

Podejrzani: Bolesław, Celina, Dorota, Halina, Ireneusz.

Zadanie

Napisz program, który:

• wczyta z pliku tekstowego POD.IN liczbę dowódców i urzędników w UOB oraz informacje o poręczeniach,
• wyznaczy listę urzędników podejrzanych o szpiegostwo,
• wyniki zapisze do pliku tekstowego POD.OUT.

Wejście

W pierwszym wierszu pliku tekstowego POD.IN zapisana jest dokładnie jedna dodatnia liczba całkowita n (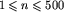) będąca liczbą pracowników UOB. Pracownicy są ponumerowani od 1 do n. W kolejnych n wierszach zapisane są opisy poręczeń. W i+1-ym wierszu pliku znajduje się opis poręczeń udzielonych pracownikowi nr i. Jest to ciąg liczb całkowitych poodzielanych pojedynczymi odstępami. Pierwsza liczba w tym ciągu, 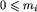, jest równa liczbie poręczeń udzielonych pracownikowi nr i. Kolejne m_i liczb to numery pracowników, którzy poręczyli za prawdomówność pracownika nr i. (Tak więc liczba wyrazów ciągu w i+1-ym wierszu wynosi m_i + 1.) Dowódcy to Ci pracownicy, za których nikt nie poręczył.

Wyjście

Twój program powinien:

• w kolejnych wierszach pliku tekstowego POD.OUT zapisać w rosnącej kolejności, po jednej liczbie w każdym wierszu, ciąg dodatnich liczb całkowitych będących numerami urzędników podejrzanych o szpiegostwo - jeżeli tacy urzędnicy są,
• w pierwszym i jedynym wierszu pliku wyjściowego POD.OUT zapisać dokładnie jedno słowo BRAK - jeżeli takich urzędników nie ma.

Przykład

9
0
1 1
1 2
2 2 3
2 1 7
1 5
0
2 7 9
2 7 8

2
3
4
8
9

Rozwiązanie

Zadanie to można w naturalny sposób wyrazić w języku teorii grafów. Mamy dany graf skierowany. Wierzchołki tego grafu reprezentują pracowników UOB, a krawędzie reprezentują poręczenia. Krawędź reprezentuje poręczenie udzielone przez pracownika v urzędnikowi u. Dowódcy są reprezentowani przez te wierzchołki, do których nie prowadzą żadne krawędzie.

Niech u będzie wierzchołkiem reprezentującym urzędnika. Jak sprawdzić czy u jest podejrzany o szpiegostwo? Zależy to od tego, ilu dowódców pośrednio poręczyło za jego lojalność. Temu, że pewien dowódca d pośrednio poręczył za lojalność urzędnika u odpowiada ścieżka prowadząca z d do u. Tak więc, jeśli istnieją przynajmniej dwa wierzchołki reprezentujące dowódców, z których możemy poprowadzić ścieżki do u, to u nie jest podejrzany o szpiegostwo - gdyby jeden z tych dowódców okazał się szpiegiem, to i tak drugi poręczył pośrednio za lojalność u. Jeżeli natomiast istnieje co najwyżej jeden wierzchołek d reprezentujący dowódcę, z którego możemy poprowadzić ścieżkę kończącą się w u, to u jest podejrzany o szpiegostwo - gdyby d okazał się szpiegiem, to wiarygodność u zostałaby podważona.

Zadanie to można rozwiązać wykorzystując przeszukiwanie grafu wszerz lub w głąb (zobacz [10] lub [10]). W najprostszej wersji możemy dla każdego urzędnika wyznaczyć liczbę dowódców, którzy pośrednio poręczyli za niego, przeszukując graf "wstecz". Podobnie, możemy dla każdego dowódcy wyznaczyć urzędników, za których on poręczył, przeszukując graf zgodnie z kierunkiem krawędzi. Rozwiązania te są jednak nieefektywne. Ich złożoność czasowa jest O(nm), gdzie n jest liczbą wierzchołków, a m jest liczbą krawędzi w grafie.

Zauważmy jednak, że nie musimy wyznaczać wszystkich dowódców, którzy pośrednio poręczyli za danego urzędnika. Jeśli znajdziemy dwóch takich dowódców, to nie musimy wyznaczać kolejnych - dany urzędnik i tak nie jest podejrzany o szpiegostwo. Również wszyscy ci, za których ten urzędnik poręczył też nie są podejrzani o szpiegostwo. Ponadto nie jest istotne, którzy dowódcy poręczyli pośrednio za danego urzędnika, a jedynie ilu.

Możemy więc każdemu urzędnikowi przyporządkować licznik określający ilu dowódców pośrednio poręczyło za niego: "żaden", "jeden", "dwóch lub więcej". Jeśli licznik jest równy jeden, to dodatkowo pamiętamy który dowódca poręczył pośrednio za urzędnika - informację tę będziemy wykorzystywać zamiast kolorowania wierzchołków w trakcie przeszukiwania grafu. Początkowo przyjmujemy, że żaden dowódca nie poręczył pośrednio za żadnego urzędnika. Następnie, dla każdego dowódcy przeszukujemy graf począwszy od niego i zwiększamy liczniki odwiedzonych urzędników. Jeśli licznik któregoś urzędnika jest równy jeden i poręczył za niego pośrednio ten dowódca, od którego zaczęliśmy przeszukiwanie grafu, to urzędnik ten był już w tym przeszukiwaniu odwiedzony. Jeśli licznik któregoś urzędnika osiągnie wartość "dwóch lub więcej', to pomijamy go przy dalszych przeszukiwaniach grafu. W ten sposób każdy wierzchołek zostanie odwiedzony co najwyżej dwa razy. W rezultacie złożoność czasowa takiego rozwiązania jest O(n + m), gdzie n jest liczbą wierzchołków, a m jest liczbą krawędzi w grafie. Złożoność pamięciowa jest takiego rzędu jak wielkość grafu i wynosi O(n + m). Rozwiązanie to może być zaimplementowane w następujący sposób:

1	const
2	N_MAX = 500; { Maksymalna liczba wierzchołków. }
3
4	ST_UNKNOWN = 0; { Brak poręczeń. }
5	{ Jedno poręczenie = nr poręczającego dowódcy. }
6	ST_CLEAN = N_MAX + 1; { Co najmniej dwa poręczenia. }
7
8	type
9	t_array = array [1..N_MAX] of word;
10	p_array = ^t_array;
11	t_official = record
12	status: word; { Licznik poręczeń. }
13	cpt: boolean; { Czy jest dowódcą? }
14	vouchees_no: word; { Liczba poręczanych urzędników. }
15	vouchees: p_array; { Poręczani urzędnicy. }
16	end
17
18	var
19	officials: array [1..N_MAX] of t_official; { Graf. }
20	n: word; { Liczba wierzchołków. }
21
22	procedure find_suspects;
23	{ Wyznacz wartości liczników poręczeń dla urzędników. }
24	var
25	i: word;
26
27	procedure go_down (no: word);
28	{ Przeszukiwanie grafu w głąb, począwszy od wierzchołka nr no. }
29	var
30	i: word;
31	captain: word;
32	begin
33	captain := officials[no].status;
34	for i := 1 to officials[no].vouchees_no do
35	with officials[officials[no].vouchees^[i]] do begin
36	if (status = ST_UNKNOWN) then begin
37	{ Pierwszy raz wchodzimy do wierzchołka. }
38	{ Przepisujemy status poprzedniego wierzchołka. }
39	status := captain;
40	go_down (officials[no].vouchees^[i])
41	end end if ((status < ST_CLEAN) and
42	(status 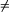captain)) then begin
43	{ Znaleźliśmy drugiego dowódcę. }
44	status := ST_CLEAN;
45	go_down (officials[no].vouchees^[i])
46	end
47	end
48	end { go_down }
49
50	begin
51	for i := 1 to n do officials[i].status := ST_UNKNOWN;
52	for i := 1 to n do if officials[i].cpt then begin
53	{ Dowódca }
54	officials[i].status := i;
55	go_down (i);
56	officials[i].status := ST_CLEAN
57	end
58	end

Testy

Do sprawdzania rozwiązań zawodników użyto 14 testów.

Większość testów ma postać: 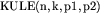, gdzie:

1. cały graf n-wierzchołkowy jest podzielony na k równolicznych podgrafów

2. każdy z podgrafów jest losowy, przy czym prawdopodobieństwo, że między danymi dwoma wierzchołkami występuje krawędź wynosi p1
3. każdy podgraf zawiera dokładnie jednego dowódcę
4. każdy podgraf zawiera jeden wyróżniony wierzchołek, który nie jest dowódcą
5. na wierzchołkach wyróżnionych znów mamy strukturę grafu, tym razem z prawdopodobieństwem wystąpienia krawędzi równym p2
6. jeśli k=1, to dodatkowo doczepiamy do grafu gadżety, które powodują, że nie wszyscy urzędnicy są podejrzani (nie chcemy trywializować testu)

POD2.IN - ,

POD3.IN - ,

POD4.IN - ,

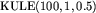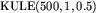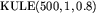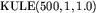POD5.IN - - duży graf pełny z gadżetami,

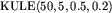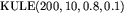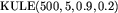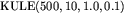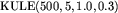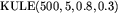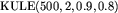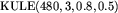POD6.IN - ,

POD7.IN - ,

POD8.IN - ,

POD9.IN - ,

POD10.IN - ,

POD11.IN - ,

POD12.IN - ,

POD13.IN - .