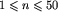Po-łamana

W prostokątnym układzie współrzędnych każdy punkt o współrzędnych całkowitych nazywamy p-punktem.

Dowolny odcinek równoległy do jednej z osi współrzędnych, o różnych końcach będących p-punktami, nazywamy p-odcinkiem. Rozważamy odcinki domknięte, tzn. końce należą do odcinka. Łamaną zbudowaną z k p-odcinków, z których każde kolejne dwa są prostopadłe, nazywamy po-łamaną stopnia k.

Zadanie

Napisz program, który:

• wczyta z pliku tekstowego POL.IN opisy pewnej liczby p-odcinków oraz współrzędne dwóch różnych p-punktów A i B,
• wyznaczy minimalny stopień po-łamanej łączącej te dwa punkty i nie przecinającej żadnego z danych p-odcinków lub stwierdzi, że taka po-łamana nie istnieje,
• zapisze wynik do pliku tekstoweg POL.OUT.

Wejście

Opis p-punktu składa się z dwóch nieujemnych liczb całkowitych oddzielonych pojedynczym odstępem, będących odpowiednio współrzędnymi x i y tego p-punktu. Liczby te należą do przedziału [0..1 000 000 000]. W pierwszym wierszu pliku wejściowego POL.IN znajduje się tylko opis p-punktu A. W drugim wierszu znajduje się tylko opis p-punktu B. W trzecim wierszu zapisana jest dokładnie jedna nieujemna liczba całkowita n będąca liczbą p-odcinków, 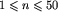. W każdym z kolejnych n wierszy znajdują się opisy dokładnie dwóch p-punktów, oddzielone pojedynczym odstępem. Są to współrzędne końców jednego p-odcinka.

Wyjście

W pierwszym i jedynym wierszu pliku tekstowego POL.OUT powinna znaleźć się jedna liczba będąca minimalnym stopniem po-łamanej łączącej punkty A i B oraz nie przecinającej żadnego z zadanych p-odcinków, lub słowo BRAK, jeśli po-łamana o powyższych własnościach nie istnieje.

\openin\tmpfile testdir.inp \ifeof\tmpfile \write16SINOL: brak pliku 'testdir.inp' \else \read\tmpfile to\sinolTestIn \ifeof\tmpfile \write16SINOL: plik 'testdir.inp' skonczyl sie zbyt wczesnie \else \read\tmpfile to\sinolTestOut \fi \fi \closein\tmpfile

Przykład

Dla pliku wejściowego POL.IN:

1 2
3 4
5
0 0 7 0
0 5 7 5
2 2 2 7
4 0 4 3
3 2 6 2

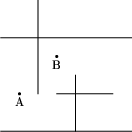
poprawną odpowiedzią jest plik wyjściowy POL.OUT:

5

Rozwiązanie wzorcowe

Niech x_1 < x_2 < ... będzie rosnąco uporządkowanym ciągiem (bez powtórzeń) współrzędnych x wszystkich końców odcinków z dodatkowo dodaną współrzędną x punktu B. Niech y_1 < y_2 < ... będzie analogicznym ciągiem dla współrzędnej y. Rozważmy podział osi 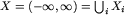, gdzie

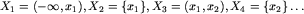
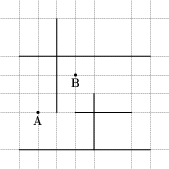
Niech P₁ i P₂ będą dwoma elementami powyższego podziału. Jeśli z pewnego punktu 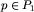istnieje łamana o ustalonym stopniu i końcu w P₂, to z każdego innego punktu P₁ także. W szczególności za P₂ można przyjąć punkt B.

Oznacza to, że punkty w jednym elemencie podziału zachowują się identycznie, jeśli chodzi o istnienie łamanych o końcu w punkcie B. Rozwiązanie w zasadzie się narzuca. Trzeba skonstruować graf, w którym wierzchołkami są elementy podziału (ma on strukturę kraty, co ułatwia implementację), krawędzie zaś oznaczają możliwość przejścia z jednego elementu do innego. Następnie w tym grafie używamy procedury przeszukiwania wszerz (BFS), aby znaleźć łamaną minimalnego stopnia łączącą element zawierający punkt A z punktem B. Musimy jednak w procedurze BFS dokonać dwu modyfikacji:

1. oddzielnie rozpatrywać wejścia pionowe i poziome, ponieważ ze względu na dalszą trasę nie są to sytuacje jednakowe,

2. po dojściu do wierzchołka "pionowo" przechodzimy nie do jego najbliższych sąsiadów, ale do wszystkich wierzchołków, do których można z niego dojść poziomo (przypadek dojścia poziomego jest analogiczny) - w ten sposób algorytm ma złożoność przeszukiwania BFS, a pierwsze dojście do punktu B od razu daje odpowiedź na postawione w zadaniu pytanie.

Testy

Do sprawdzenia rozwiązań zawodników użyto 12 testów: