 . Należy znaleźć długość najdłuższego słowa występującego jako spójny fragment w każdym z danych słów.
. Należy znaleźć długość najdłuższego słowa występującego jako spójny fragment w każdym z danych słów. Dany jest ciąg słów nad alfabetem  . Należy znaleźć długość najdłuższego słowa występującego jako spójny fragment w każdym z danych słów.
. Należy znaleźć długość najdłuższego słowa występującego jako spójny fragment w każdym z danych słów.
Napisz program, który:
W pierwszym wierszu pliku tekstowego POW.IN zapisano liczbę n, gdzie 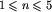 , oznaczającą liczbę słów. W każdym z n kolejnych wierszy znajduje się jedno słowo utworzone z małych liter alfabetu angielskiego 'a',...,'z'. Każde ze słów ma długość przynajmniej 1, ale nie większą niż 2 000.
, oznaczającą liczbę słów. W każdym z n kolejnych wierszy znajduje się jedno słowo utworzone z małych liter alfabetu angielskiego 'a',...,'z'. Każde ze słów ma długość przynajmniej 1, ale nie większą niż 2 000.
Plik tekstowy POW.OUT powinien zawierać dokładnie jeden wiersz zawierający pojedynczą liczbę całkowitą równą długości najdłuższego słowa występującego jako spójny fragment w każdym z danych słów.
3 abcb bca acbcpoprawną odpowiedzią jest plik wyjściowy POW.OUT
2
Do rozwiązania zadania posłuży nam adaptacja struktury danych zwanej phsłownikiem podsłów bazowych. Słownik podsłów bazowych to z grubsza rzecz biorąc tablica phnazw wszystkich podsłów danego słowa o długościach będących potęgami dwójki, przy czym takie same podsłowa mają te same nazwy, a różne podsłowa o tej samej długości - różne nazwy (nazwa to po prostu liczba całkowita z zakresu od 1 do długości słowa; num[i,k] to nazwa podsłowa o długości 2k zaczynającego się na pozycji i w danym słowie). Taka informacja umożliwia nam sprawdzenie w czasie stałym, czy dwa podsłowa tej samej długości są jednakowe, nawet jeśli ich długości nie są potęgami dwójki: nazwą identyfikującą jednoznacznie podsłowo długości r (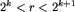 ) zaczynające się na pozycji i jest para
) zaczynające się na pozycji i jest para  num[i,k], num[
num[i,k], num[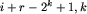 ]
] . Rozmiar tej struktury danych, to oczywiście
. Rozmiar tej struktury danych, to oczywiście 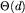 , gdzie d jest długością słowa, i można ją skonstruować w takim właśnie czasie phmetodą wstępującą (ang. bottom-up):
, gdzie d jest długością słowa, i można ją skonstruować w takim właśnie czasie phmetodą wstępującą (ang. bottom-up):
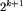 zaczynającemu się na pozycji i, gdzie
zaczynającemu się na pozycji i, gdzie 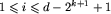 , nadajemy tymczasową nazwę
, nadajemy tymczasową nazwę  num[i,k], num[
num[i,k], num[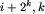 ]
] . Jest to dobra, unikalna nazwa - tyle, że nie jest liczbą z zakresu od 1 do d, lecz parą takich liczb.
. Jest to dobra, unikalna nazwa - tyle, że nie jest liczbą z zakresu od 1 do d, lecz parą takich liczb.
Czas wypełniania każdego wiersza jest liniowy, a liczba wierszy do wypełnienia to 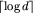 . Szczegóły konstrukcji można znaleźć w książce [10].
. Szczegóły konstrukcji można znaleźć w książce [10].
W rozwiązaniu wzorcowym obliczamy phwspólny słownik dla wszystkich zadanych słów, sklejonych w jedno długie słowo z separatorami (specjalnymi znakami występującymi tylko jednokrotnie) na granicach słów wejściowych. Separatory wprowadzamy po to, żeby uniknąć odrębnego analizowania podsłów "przechodzących przez granice" słów wejściowych. Żeby zaoszczędzić pamięć, przechowujemy tylko jeden, ostatnio obliczony wiersz tablicy num. Schemat postępowania wygląda następująco:
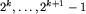 , to jej dokładną wartość wyznaczamy metodą bisekcji w k krokach. (Zachodzi tu potrzeba wyznaczenia nazw dla podsłów o długości p na podstawie nazw dla podsłów o długości r, gdzie r<p<2r. Robimy to, posługując się opisaną na początku sztuczką, czyli jako nazwę tymczasową biorąc parę nazw zachodzących na siebie podsłów długości r pokrywających podsłowo długości p.)
, to jej dokładną wartość wyznaczamy metodą bisekcji w k krokach. (Zachodzi tu potrzeba wyznaczenia nazw dla podsłów o długości p na podstawie nazw dla podsłów o długości r, gdzie r<p<2r. Robimy to, posługując się opisaną na początku sztuczką, czyli jako nazwę tymczasową biorąc parę nazw zachodzących na siebie podsłów długości r pokrywających podsłowo długości p.)
Przedstawione tu rozwiązanie nie jest optymalne. Postawiony w zadaniu problem można rozwiązać w czasie phliniowym względem sumy długości słów wejściowych. Wymaga to jednak użycia dość wyrafinowanych struktur danych (np. phdrzew sufiksowych), raczej trudnych do zaimplementowania podczas pięciogodzinnej sesji. W dodatku stopień komplikacji tych struktur mógłby spowodować na tyle duże stałe narzuty czasowe, że przy określonych w zadaniu ograniczeniach na rozmiar danych wejściowych, rozwiązanie asymptotycznie optymalne byłoby przy testowaniu trudne do odróżnienia lub wręcz gorsze, od znacznie prostszego rozwiązania opisanego powyżej.
Do sprawdzenia rozwiązań zawodników użyto 14 testów, niekiedy łączonych w grupy.