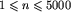Promocja

Wielka bajtocka sieć supermarketów poprosiła Cię o napisanie programu symulującego koszty właśnie przygotowywanej promocji.

Przygotowywana promocja ma mieć następujące zasady:

• klient, który chce wziąć udział w promocji, wpisuje na zapłaconym przez siebie rachunku swoje dane i wrzuca go do specjalnej urny,
• pod koniec każdego dnia promocji z urny wyciągane są dwa rachunki:
  • najpierw wybierany jest rachunek opiewający na największą kwotę,
  • następnie wybierany jest rachunek opiewający na najmniejszą kwotę;
  
     klient, który zapłacił największy rachunek otrzymuje nagrodę pieniężną równą różnicy pomiędzy wysokością jego rachunku, a wysokością rachunku opiewającego na najmniejszą kwotę,
• aby uniknąć kilkukrotnych nagród za jeden zakup, oba wybrane wg reguł z poprzedniego punktu rachunki nie wracają już do urny, ale wszystkie pozostałe rachunki dalej biorą udział w promocji.

Obroty supermarketu są bardzo duże, możesz więc założyć, że pod koniec każdego dnia, przed wyciągnięciem rachunków opiewających na największą i najmniejszą kwotę, w urnie znajdują się co najmniej 2 rachunki.

Twoim zadaniem jest obliczenie na podstawie informacji o wysokościach rachunków wrzucanych do urny w poszczególnych dniach promocji, jaki będzie łączny koszt nagród w całej promocji.

Zadanie

Napisz program, który:

• wczyta z pliku tekstowego PRO.IN listę wysokości rachunków wrzucanych do urny w poszczególnych dniach promocji,
• obliczy łączny koszt nagród wypłacanych w kolejnych dniach promocji,
• zapisze wynik w pliku tekstowym PRO.OUT.

Wejście

W pierwszym wierszu pliku tekstowego PRO.IN znajduje się jedna dodatnia liczba całkowita n, gdzie 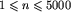, oznaczająca czas trwania promocji w dniach.

W każdym z kolejnych n wierszy znajduje się ciąg nieujemnych liczb całkowitych pooddzielanych pojedynczymi odstępami. Liczby w (i+1)-szym wierszu pliku określają wysokości rachunków wrzuconych do urny w i-tym dniu promocji. Pierwsza w wierszu liczba k, 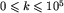, jest liczbą rachunków z danego dnia, a kolejne k liczb to dodatnie liczby całkowite będące wysokościami poszczególnych rachunków, każda z tych liczb jest nie większa niż 10⁶.

Łączna liczba rachunków wrzuconych do urny podczas całej promocji nie przekracza 10⁶.

Wyjście

Plik tekstowy PRO.OUT powinien zawierać dokładnie jedną liczbę całkowitą równą łącznemu kosztowi nagród wypłacanych podczas całej promocji.

Przykład

5
3 1 2 3
2 1 1
4 10 5 5 1
0
1 2

19

Rozwiązanie

Przy rozwiązaniu tego zadania bardzo pomocna będzie struktura danych umożliwiająca wykonywanie następujących operacji:

  ADD(x) - dodanie elementu x do struktury;   MIN - podanie wartości minimalnego elementu w strukturze;   MAX - podanie wartości maksymalnego element w strukturze;   ExtractMin - usunięcie minimalnego elementu;   ExtractMax - usunięcie maksymalnego elementu.

Zwykły kopiec (zob. [13]) oferuje efektywną implementację trzech z tych operacji: ADD, MIN, ExtractMin (lub ADD, MAX, ExtractMax). Rozwiązaniem może być struktura składającą się z dwóch połączonych kopców, jeden z nich udostępnia operacje ADD, MIN, ExtractMin, natomiast drugi ADD, MAX, ExtractMax. W takim rozwiązaniu decydujemy się na pewną rozrzutność i każdy element należący do struktury będziemy pamiętać podwójnie: w pierwszym i drugim kopcu, dodatkowo z każdym elementem jest związany wskaźnik do bliźniaczego elementu w drugim kopcu. Operacje MIN, MAX odwołują się do odpowiednich kopców i wymagają stałego czasu. Operacja ADD wymaga dodania elementu do obu kopców, oraz uaktualnienia wskaźników, i tak jak w zwykłym kopcu wymaga czasu O(logn). Operacje ExtractMin, ExtractMax sprowadzają się do wykonania odpowiedniej operacji na odpowiednim kopcu (tym który oferuje tę operację), oraz usunięciu elementu bliźniaczego z drugiego kopca (ponieważ pamiętamy wskaźnik do tego elementu, możemy wykonać i tę operację w czasie O(logn)). Zatem całość również wymaga czasu O(logn). Przy wszystkich modyfikacjach, należy zwracać baczną uwagę na uaktualnianie wskaźników między oboma kopcami.

Rozwiązanie 1

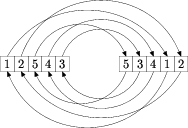
Mając do dyspozycji powyższą stukturę danych, schemat algorytmu jest już oczywisty. Dla każdego dnia dodajemy do struktury rachunki, a następnie wyjmujemy z niej jeden największy i jeden najmniejszy, oraz odpowiednio zwiększamy całkowity koszt promocji.

Niestety takie rozwiązanie, ze względu na bardzo dużą liczbę rachunków, które mogły pojawić się w promocji, nie jest akceptowalne ze względu na ogranicznia pamięciowe. Należy zastanowić się, jakie rachunki na pewno nie mają szans na wyjęcie z urny. Można spostrzec, że gdy mamy w strukturze więcej niż 2n rachunków, to szanse na wyciągnięcie z urny ma jedynie n największych i n najmniejszych, natomiast wszystkie pozostałe, "środkowe" rachunki, nie mają już takiej szansy i można je pominąć. To spostrzeżenie prowadzi już do ulepszonego rozwiązania, które będzie wymagać jedynie pamięci rzędu O(n).

Rozwiązanie 2

• Dopóki liczba rachunków w strukturze S nie przekracza 2n stosuj rozwiązanie 1.
• Jeśli liczba rachunków osiągnie 2n, przepisz n najmiejszych do struktury S_min, natomiast n największych do struktury S_max. Strukturę S można już usunąc, natomiast wszystkie dalsze operację będą wykonywane na S_min i S_max. Dodawanie nowego rachunku x wygląda następująco:
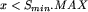  • jeśli , to usuwamy z S_min element 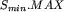(operacja 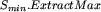) i dodajemy x do S_min;
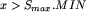  • jeśli , to postępujemy symetrycznie jak w poprzednim przypadku (zamieniając MAX na MIN i S_min na S_max);
  • w przeciwnym przypadku możemy zapomnieć o tym rachunku.
  Chcąc wydobyć rachunek o najmniejszej wartości wykonujemy operację ExtractMin na S_min i analogicznie, chcąc otrzymać rachunek o największej wartości wykonujemy operację ExtractMax na S_max.

Testy

Do sprawdzania rozwiązań zawodników użyto 10 testów opisanych poniżej: