Wojciech Rytter (treść, opracowanie) Tomasz Waleń (program wzorcowy)
Trójramienny dźwig
Trójramienny dźwig ustawia kontenery na wagonach kolejowych. Wagony są ponumerowane kolejno 1, 2, .... Na każdym wagonie można postawić co najwyżej jeden kontener. W jednym ruchu dźwig pobiera ze składowiska trzy kontenery i ustawia je na wagonach o numerach i, i+p oraz i+p+q, albo na wagonach o numerach i, i+q oraz i+p+q (dla pewnych stałych 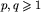 ). Dźwig trzeba zaprogramować tak, żeby załadował kontenerami pierwsze n wagonów pociągu (pociąg ma n+p+q wagonów). Program składa się z ciągu instrukcji. Każda z instrukcji opisuje jeden ruch dźwigu. Instrukcja programu ma postać trójki (x,y,z), gdzie
). Dźwig trzeba zaprogramować tak, żeby załadował kontenerami pierwsze n wagonów pociągu (pociąg ma n+p+q wagonów). Program składa się z ciągu instrukcji. Każda z instrukcji opisuje jeden ruch dźwigu. Instrukcja programu ma postać trójki (x,y,z), gdzie 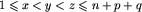 , i określa numery wagonów, na które dźwig ma ustawić kontenery. Jeżeli po wykonaniu programu na każdym spośród n pierwszych wagonów pociągu znajduje się dokładnie jeden kontener, to mówimy, że program jest poprawny.
, i określa numery wagonów, na które dźwig ma ustawić kontenery. Jeżeli po wykonaniu programu na każdym spośród n pierwszych wagonów pociągu znajduje się dokładnie jeden kontener, to mówimy, że program jest poprawny.
Zadanie
Napisz program, który:
- z pliku tekstowego TRO.IN wczyta charakterystykę dźwigu (liczby p i q) oraz liczbę wagonów do załadowania (n),
- wygeneruje poprawny program dla dźwigu,
- zapisze go do pliku tekstowego TRO.OUT.
Wejście
W pierwszym i jedynym wierszu pliku tekstowego TRO.IN znajdują się dokładnie trzy dodatnie liczby całkowite pooddzielane pojedynczymi odstępami. Są to odpowiednio: liczby p i q określające parametry dźwigu oraz liczba n, będąca liczbą początkowych wagonów pociągu do załadowania. Liczby te spełniają nierówności 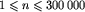 ,
, 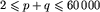 .
.
Wyjście
W pierwszym wierszu pliku tekstowego TRO.OUT powinna znajdować się dokładnie jedna liczba całkowita m będąca liczbą instrukcji w wygenerowanym programie. W każdym z kolejnych m wierszy powinny znajdować się dokładnie trzy liczby naturalne x, y, z pooddzielane pojedynczymi odstępami, 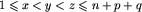 ,
, 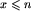 ,
, 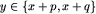 , z = x+p+q. Są to numery wagonów, na które dźwig ma położyć kontenery w kolejnym ruchu.
, z = x+p+q. Są to numery wagonów, na które dźwig ma położyć kontenery w kolejnym ruchu.
Przykład
Dla pliku wejściowego TRO.IN
2 3 10
poprawną odpowiedzią jest plik wyjściowy TRO.OUT
4
1 3 6
2 4 7
5 8 10
9 11 14
Rozwiązanie
Przyjmijmy, że 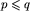 . Ruch typu i,i+p,i+p+q nazwijmy ruchem typu 1, a i,i+q,i+p+q ruchem typu 2, gdzie i jest najmniejszym numerem wolnego wagonu.
. Ruch typu i,i+p,i+p+q nazwijmy ruchem typu 1, a i,i+q,i+p+q ruchem typu 2, gdzie i jest najmniejszym numerem wolnego wagonu.
Opis algorytmu
Rozwiązanie polega na wykonywaniu tak długo jak to możliwe, ruchów typu 1, a gdy to nie jest możliwe ruchu typu 2. Okazuje się, że takie rozwiązanie zawsze generuje prawidłowy program.
Złożoność czasowa takiego algorytmu wynosi O(n+p+q), pamięciowa - O(p+q).
Rys. 1. Przykładowa historia działania dźwigu trójramiennego. W każde pole wpisany jest kolejny numer ruchu, w którym to pole zostaje zajęte. Jedynie 7-my ruch jest typu 2.
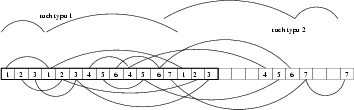
Na przykład, jeśli charakterystyką dźwigu jest (3,10) oraz n=16, to jeden z możliwych programów dźwigu jest przedstawiony na rysunku 1.
Dowód poprawności
Załóżmy, że dla pewnego wagonu i=s po raz pierwszy nie można wykonać żadnego z ruchów. Łatwo zauważyć, że wagon i+p+q jest wolny. Również s jest wolny, natomiast s+p, s+q są zajęte, ponieważ nie można wykonać ruchu. Wagon s+q został zajęty w czasie wykonywania ruchu typu 2 dla pozycji j =s-p. Ale z tego wynika, że w momencie wykonywania ruchu dla i=j wolne były i, j+p, j+p+q, zatem można było wykonać ruch typu 1, który ma priorytet i zająć pozycje j, s, s+q. Pozycja s nie może być zatem wolna - sprzeczność.
Obserwacja
Można się zastanowić nad podobnym problem dla dźwigu czteroramiennego. Jest to trudne zadanie, ponieważ najpierw dla danego n trzeba sprawdzić, czy w ogóle istnieje odpowiedni program dźwigu - nie każdy ciąg kolejnych n liczb da się wtedy "pokryć". Na przykład nie ma pokrycia dla n=3 i dźwigu o charakterystyce (1, 2, 1), tzn. takiego który zapełnia wagony i, i+1, i+3, i+4.
Testy
Do sprawdzania rozwiązań zawodników użyto 24 testów, których charakterystyki znajdują się poniżej.
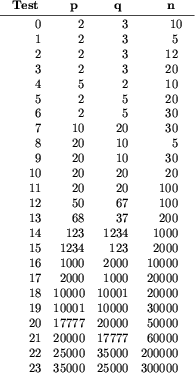
Następujące testy zostały zgrupowane: (1,2 i 3), (4,5 i 6), (7,8 i 9), (10 i 11), (12 i 13), (14 i 15), (16 i 17), (18 i 19), (20 i 21), (22 i 23).
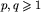 ). Dźwig trzeba zaprogramować tak, żeby załadował kontenerami pierwsze n wagonów pociągu (pociąg ma n+p+q wagonów). Program składa się z ciągu instrukcji. Każda z instrukcji opisuje jeden ruch dźwigu. Instrukcja programu ma postać trójki (x,y,z), gdzie
). Dźwig trzeba zaprogramować tak, żeby załadował kontenerami pierwsze n wagonów pociągu (pociąg ma n+p+q wagonów). Program składa się z ciągu instrukcji. Każda z instrukcji opisuje jeden ruch dźwigu. Instrukcja programu ma postać trójki (x,y,z), gdzie 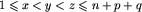 , i określa numery wagonów, na które dźwig ma ustawić kontenery. Jeżeli po wykonaniu programu na każdym spośród n pierwszych wagonów pociągu znajduje się dokładnie jeden kontener, to mówimy, że program jest poprawny.
, i określa numery wagonów, na które dźwig ma ustawić kontenery. Jeżeli po wykonaniu programu na każdym spośród n pierwszych wagonów pociągu znajduje się dokładnie jeden kontener, to mówimy, że program jest poprawny.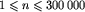 ,
, 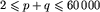 .
.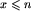 ,
, 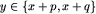 , z = x+p+q. Są to numery wagonów, na które dźwig ma położyć kontenery w kolejnym ruchu.
, z = x+p+q. Są to numery wagonów, na które dźwig ma położyć kontenery w kolejnym ruchu.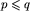 . Ruch typu i,i+p,i+p+q nazwijmy ruchem typu 1, a i,i+q,i+p+q ruchem typu 2, gdzie i jest najmniejszym numerem wolnego wagonu.
. Ruch typu i,i+p,i+p+q nazwijmy ruchem typu 1, a i,i+q,i+p+q ruchem typu 2, gdzie i jest najmniejszym numerem wolnego wagonu.
