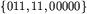 nieskończonym, bezpiecznym ciągiem jest 010101.... Dla zbioru kodów
nieskończonym, bezpiecznym ciągiem jest 010101.... Dla zbioru kodów 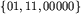 nie istnieje nieskończony, bezpieczny ciąg zer i jedynek.
nie istnieje nieskończony, bezpieczny ciąg zer i jedynek.Komisja Badania Wirusów Binarnych wykryła, że pewne ciągi zer i jedynek są kodami wirusów. Komisja wyodrębniła zbiór wszystkich kodów wirusów. Ciąg zer i jedynek nazywamy bezpiecznym, gdy żaden jego segment (tj. ciąg kolejnych wyrazów) nie jest kodem wirusa. Komisja dąży do ustalenia, czy istnieje nieskończony, bezpieczny ciąg zer i jedynek.
Dla zbioru kodów 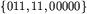 nieskończonym, bezpiecznym ciągiem jest 010101.... Dla zbioru kodów
nieskończonym, bezpiecznym ciągiem jest 010101.... Dla zbioru kodów 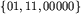 nie istnieje nieskończony, bezpieczny ciąg zer i jedynek.
nie istnieje nieskończony, bezpieczny ciąg zer i jedynek.
Napisz program, który:
W pierwszym wierszu pliku wejściowego WIR.IN znajduje się jedna liczba całkowita n będąca liczbą wszystkich kodów wirusów.
W każdym z kolejnych n wierszy znajduje się jedno niepuste słowo złożone ze znaków 0 i 1 - kod wirusa. Sumaryczna długość wszystkich słów nie przekracza 30000.
W pierwszym i jedynym wierszu pliku wyjściowego WIR.OUT powinno znajdować się słowo:
3 01 11 00000poprawną odpowiedzią jest plik wyjściowy WIR.OUT
NIE
W rozwiązaniu zadania najważniejszą rolę odgrywają sufiksy i prefiksy wirusów. Jeśli słowo  można zapisać jako złożenie trzech słów
można zapisać jako złożenie trzech słów 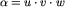 , to u nazywamy prefiksem, a w sufiksem
, to u nazywamy prefiksem, a w sufiksem  . Na przykład prefiksami słowa rytter są
. Na przykład prefiksami słowa rytter są 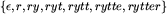 , a sufiksami
, a sufiksami 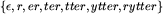 , gdzie
, gdzie  oznacza słowo puste o długości zero.
oznacza słowo puste o długości zero.
Dla słowa  i zbioru słów-wirusów W, przez
i zbioru słów-wirusów W, przez 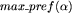 oznaczmy najdłuższy sufiks
oznaczmy najdłuższy sufiks  , który jest jednocześnie prefiksem pewnego wirusa z W. Jeśli chcemy sprawdzić, czy dany ciąg binarny nie zawiera wirusa, to wystarczy przeglądać ten ciąg znak po znaku i pamiętać jedynie ostatni istotny fragment. Tym istotnym fragmentem jest maksymalny prefiks wirusa, zatem po wczytaniu ciągu a_1a_2a_3 ... a_k pamiętamy
, który jest jednocześnie prefiksem pewnego wirusa z W. Jeśli chcemy sprawdzić, czy dany ciąg binarny nie zawiera wirusa, to wystarczy przeglądać ten ciąg znak po znaku i pamiętać jedynie ostatni istotny fragment. Tym istotnym fragmentem jest maksymalny prefiks wirusa, zatem po wczytaniu ciągu a_1a_2a_3 ... a_k pamiętamy 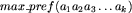 . Słowo a_1a_2a_3 ... a_n jest bezpieczne, gdy każdy z pośrednich istotnych fragmentów jest bezpieczny, tzn. gdy
. Słowo a_1a_2a_3 ... a_n jest bezpieczne, gdy każdy z pośrednich istotnych fragmentów jest bezpieczny, tzn. gdy
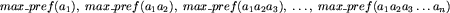
Motywuje to wprowadzenie pomocniczego grafu G, którego ścieżki odpowiadają dokładnie wszystkim możliwym bezpiecznym słowom i którego węzłami są wszystkie bezpieczne prefiksy wirusów. Od węzła x prowadzimy skierowaną krawędź do y, gdy dla pewnej litery a (gdzie a=0 lub a=1) po dopisaniu jej do x otrzymamy słowo takie, że maksymalnym jego sufiksem, który jest prefiksem pewnego wirusa, jest y. Oznaczmy y przez 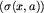 . Można to zapisać bardziej formalnie:
. Można to zapisać bardziej formalnie:
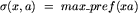 , gdy xa jest bezpieczny,
, gdy xa jest bezpieczny,
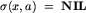 , gdy xa nie jest bezpieczny (NIL oznacza brak krawędzi).
, gdy xa nie jest bezpieczny (NIL oznacza brak krawędzi).
Rysunek 2 przedstawia graf G dla przykładowego zbioru wirusów
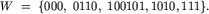
Grafy tego typu odpowiadają w teorii obliczeń tzw. automatom skończonym. Zbiór W jest bezpieczny wtedy i tylko wtedy, gdy w grafie G istnieje cykl skierowany osiągalny z węzła startowego odpowiadającego słowu pustemu. Każda ścieżka w tym grafie zaczynająca się od węzła startowego wyznacza ciąg bezpieczny.
Pierwszym krokiem w konstrukcji grafu G jest zbudowanie drzewa właściwych prefiksów wirusów, tzn. takich prefiksów słów ze zbioru W, które nie są równe żadnemu wirusowi. Drzewo dla przykładowego zbioru W jest przedstawione na rysunku 1.
Uwaga: Załóżmy początkowo, że żaden wzorzec nie jest właściwym podsłowem innego wzorca.
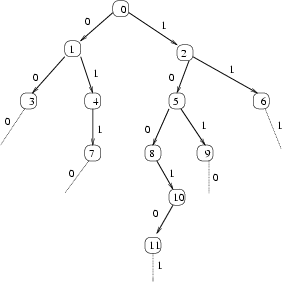
Wierzchołki są ponumerowane, jednakże każdy węzeł utożsamiamy z pewnym prefiksem wzorca. Załóżmy, że syn(x,a) oznacza węzeł xa, jeśli xa jest bezpiecznym prefiksem wzorca. Jeśli 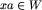 , to syn(x,a) = N, gdzie N jest specjalną wartością oznaczającą, że krawędzi etykietownej symbolem a z węzła x nigdy być nie może. W pozostałych przypadkach syn(x,a) = NIL.
, to syn(x,a) = N, gdzie N jest specjalną wartością oznaczającą, że krawędzi etykietownej symbolem a z węzła x nigdy być nie może. W pozostałych przypadkach syn(x,a) = NIL.
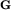
Algorytm korzysta istotnie z drzewa prefiksów T zbudowanego wcześniej i opisanego funkcją syn.
Algorytm
Inicjujemy 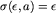 ,
, 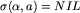 , dla a=0,1 i
, dla a=0,1 i 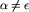 (słowa
(słowa  odpowiadają węzłom w drzewie).
odpowiadają węzłom w drzewie).
Przechodząc drzewo T wszerz, dla każdego węzła 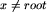 wykonaj:
wykonaj:
| 1 | niech y oraz a będą takie, że x = syn(y,a); |
| 2 | if 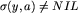 then begin then begin |
| 3 | 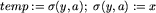 ; ; |
| 4 | for b:=0 to 1 do begin |
| 5 | if syn(x,b)=N  syn(temp,b)=N then syn(temp,b)=N then |
| 6 | 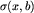 :=NIL :=NIL |
| 7 | end if 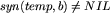 then then |
| 8 | 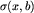 :=syn(temp,b) :=syn(temp,b) |
| 9 | end 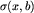 := :=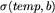 |
| 10 | end |
| 11 | end |
Na zakończenie algorytmu należy ograniczyć graf G do jego podgrafu indukowanego przez wierzchołki osiągalne z wierzchołka startowego.
Uwaga: Założenie, że żaden wirus nie jest podsłowem innego wirusa było użyteczne przy wprowadzeniu pomocniczego drzewa prefiksów. Algorytm konstrukcji grafu automatycznie wykrywa takie sytuacje, tak więc założenie to nie jest istotne.
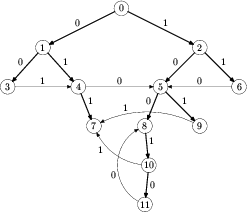
Aby stwierdzić, czy w grafie jest cykl należy sprawdzić, czy wierzchołki grafu można posortować topologicznie. Można zastosować dwie alternatywne metody:
Nie opisujemy dokładnie tych metod ponieważ sprawdzanie acykliczności grafu wystąpiło już w wielu poprzednich zadaniach olimpijskich.
Dla naszego przykładowego zbioru wirusów nieskończona ścieżka "idąca" po węzłach grafu G.
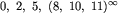
odpowiada nieskończonemu bezpiecznemu słowu:
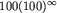
Wprowadzamy dwie operacje na zbiorze W. Niech 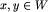 .
.
Usuwanie y. Jeśli x jest podsłowem y, to y usuwamy z W.
Skracanie y. Jeśli y = za, gdzie 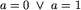 , oraz
, oraz  i u jest sufiksem z, to y:=z.
i u jest sufiksem z, to y:=z.
Symbol  oznacza 1-a.
oznacza 1-a.
Na przykład jeśli x = 0010, y = 001010011, to skracając y dostajemy y=00101001.
Operację skracania możemy zastosować dlatego, że jeśli w pewnym nieskończonym ciągu wystąpi skrócone y, to albo w tym ciągu wystąpi samo y, albo x.
Niech W' będzie zbiorem powstałym z W za pomocą jednej z tych operacji, wtedy:
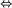 W' jest bezpieczny.
W' jest bezpieczny.Można wówczas skonstruować dowolnie długi bezpieczny ciąg postępując w następujący sposób: zaczynamy od ciągu pustego i dokładamy po jednym symbolu, do chwili gdy otrzymujemy ciąg niebezpieczny (gdy sufiks należy do w); zamieniamy ostatnio dodany symbol na przeciwny i kontynuujemy naszą konstrukcję. Nasz algorytm polega na stosowaniu w dowolnej kolejności jednej z powyższych operacji, aż otrzymany zbiór zawierający obie litery 0,1, albo zbiór zawierający dłuższe słowo, który to zbiór nie da się dalej zmienić za pomocą jednej z naszych operacji. W pierwszym przypadku W jest niebezpieczny. Dla naszego przykładowego zbioru wirusów W z rysunku 1 od razu widać, że jest on bezpieczny, ponieważ żadna z dwóch operacji się do niego nie stosuje.
Rozważmy przykład zbioru, który nie jest bezpieczny. W poniższym ciągu przekształceń podkreślamy słowo biorące udział w przekształceniu, słowo to jest usuwane lub skracane o jeden symbol od końca. 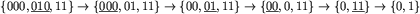 .
.
Zatem 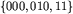 jest niebezpieczny, gdyż końcowy zbiór
jest niebezpieczny, gdyż końcowy zbiór 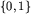 jest niebezpieczny.
jest niebezpieczny.
Do sprawdzania rozwiązań zawodników użyto 10 testów: