


| About Olympic -> Problems -> II OI 1994/1995 |  |

|
II Olympiad in Informatics 1994/1995
|
|
Task: DRZ
|
Author: Krzysztof Diks
|
| III stage contest |
A graph is a pair (V, E), where V is a finite set of elements called vertices of the graph, and E is a subset of the set of all unordered pairs of distinct vertices. The elements of the set E are called edges of the graph. If for each pair of distinct vertices u, v there exists exactly one sequence of distinct vertices w0, w1, ..., wk, such that w0 = u, wk = v and the pairs {wi, wi + 1} are in E, for i = 0, ..., k - 1, then the graph is called a tree. We say that the distance between the vertices u and v in the tree is k.
It is known that a tree of n vertices has exactly n - 1 edges. A tree T whose vertices are numbered from 1 to n can be unambiguously described by giving the number of its vertices n, and an appropriate sequence of n - 1 pairs of positive integers describing its edges.
Any permutation of vertices - i.e. a sequence in which each vertex appears exactly once - is called a traversing order of a tree. If the distance of each two consecutive vertices in some order of the tree T is at most c, then we say that it is a traversing order of the tree with step c.
It is known that for each tree its traversing order with step 3 can be found.
Example
The picture shows a tree of 7 vertices. The vertices are represented by black dots, and edges by line segments joining the dots.
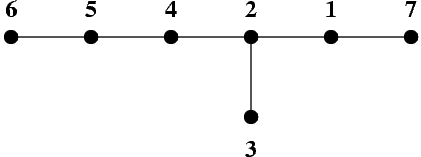
This tree can be traversed with step 3 by visiting its vertices in the following order: 7 2 3 5 6 4 1.
Task
Write a program that:- reads a description of a tree from the text file DRZ.IN,
- finds an arbitrary traversing order of that tree with step 3,
- writes that order in the text file DRZ.OUT.
Input
- In the first line of the file DRZ.IN there is a positive integer n, not greater than 5000 - it is the number of vertices of the tree.
- In each of the following n - 1 lines there is one pair of positive integers separated by a single space and representing one edge of the tree.
Output
In the successive lines of the file DRZ.OUT one should write the numbers of the successive vertices in a traversing order of the tree with step 3 - each number should be written in a separate line.Example
The following file DRZ.IN is a correct description of the tree presented in the picture:7 1 2 2 3 2 4 4 5 5 6 1 7The following file DRZ.OUT is a correct solution:
7 2 3 5 6 4 1
Your program should look for the file DRZ.IN in the current directory
and create the file DRZ.OUT also in the current directory. The source
file containing the program written by you should be named DRZ.???,
where ??? are substituted by at most three-letter abbreviation of the
programming language used. The same program in an executable form
should be written in a file DRZ.EXE.

Print friendly version

