


| About Olympic -> Problems -> XII OI 2004/2005 |  |

Task: Two parties
King Byteasar has decided to throw two great parties and wants to invite to them every single Byteotian inhabitant. Of course he wants to invite each of them to exactly one of the parties. The king knows from his own vast experience that a person is having a good time when there is an even number of her/his friends at the party. Thus he has asked you to divide the country's inhabitants between two parties in a way that as many people as possible have an even number of friends at their party. A trivial division, i.e. one that leaves one party with no guests invited, is allowed. The acquaintanceship is a symmetric relation, i.e. whenever a person A knows the person B, the person B also knows the person A.
Task
Write a programme that:- reads from the standard input the number of Byteotia's inhabitants and the description of their acquaintances,
- splits the habitants into two parties in such way that the number of people who have an even number of friends at their party is as large as possible,
- writes to the standard output a list of people who should be invited to the first party.
Input
In the first line of the standard input there is one integer N ( 1 <= N <= 200) -- it is the number of inhabitants of Byteotia. The habitants are numbered from 1 to N. In the following N lines there are the descriptions of subsequent persons' acquaintances. At the beginning of the (i + 1)th line there is an integer li ( 0 <= li <= N - 1) -- the number of friends of the ith inhabitant. It is followed by li pairwise distinct numbers of the ith inhabitant's friends. We assume that no inhabitant is her/his own friend. It follows that each acquaintance is written twice: if A and B know each other, then B appears on A's list of friends and A appears on B's.
Output
In the first line of the standard output your programme should write one integer M -- the number of people who are to come to the first party. In the second line the M numbers of these people should be written. The rest shall come to the second party.There are many correct divisions in this task -- your programme should write any one of them.
Example
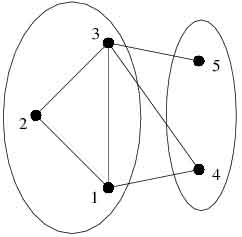
In the above example everyone will have even number of friends at the party.

Print friendly version

