


| About Olympic -> Problems -> XIII OI 2005/2006 |  |

Task: Professor Szu
Memory limit: 32MB
The Byteotian University is situated in the city of Byteion. Apart from the main building the university owns n cottages for its academic staff. The cottages are connected with one-way alleys, however, there could be more than one alley between any two cottages (the alley can also form a loop connecting a building to itself). There are also alleys connecting the cottages to the main building. Byteion has been constructed so that no two alleys intersect in a point different from a cottage or the main building (there can however be bridges or tunnels on alleys). Moreover, each and every alley starts and ends in a cottage or the main building. A route exists between each of the cottages and the main building.
Once upon a time, the Byteotian University fancied to hire a well-known computer science pundit - professor Szu. As most outstanding scientists professor Szu has a certain peculiarity to him: each day he wishes to go to the university using a different route (a route being a sequence of alleys, each starting at the cottage the previous one ended at; the main building and each of the cottages may be visited many times). The professor considers two routes distinct if they differ by at least one alley (the order matters; two different alleys connecting the very same two cottages are considered distinct).
Knowing the diagram of connections help the university in finding a cottage which has the greatest number of different routes to the main building possible (staying in such a cottage professor Szu will spend the longest time working at the university). Should there be more than one such cottage - find all of them. Should there be more than 36 500 possible routes between a certain cottage and the main building we will assume that professor Szu can stay in this particular cottage forever (as he surely cannot live infinitely and 100 years seems a safe guess).
Task
Write a programme which:- reads from the standard input the diagram of connections between the cottages of Byteion.
- determines the cottages which Professor Szu could live the longest time in and the longest possible time of habitation.
- writes the outcome to the standard output.
Input
The first line of the standard input contains two integers n and m ( 1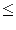 n, m
n, m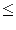 1 000 000)
separated by a single space denoting the number of cottages and alleys in Byteion, respectively
(the cottages are numbered from 1 to n,
and the university main building is denoted by n + 1).
In the following lines (2 to m + 1) there are pairs of integers
ai, bi (
1
1 000 000)
separated by a single space denoting the number of cottages and alleys in Byteion, respectively
(the cottages are numbered from 1 to n,
and the university main building is denoted by n + 1).
In the following lines (2 to m + 1) there are pairs of integers
ai, bi (
1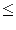 ai, bi
ai, bi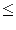 n + 1 for
1
n + 1 for
1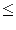 i
i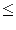 m)
separated by single spaces denoting the number of the cottage which the i-th alley starts at and the number of the cottage which the i-th alley ends at, respectively.
m)
separated by single spaces denoting the number of the cottage which the i-th alley starts at and the number of the cottage which the i-th alley ends at, respectively.
Output
The first line of the standard output should contain the largest number of days that professor Szu could spend in Byteion or a single word ''zawsze'' (Always in Polish) should this number exceed 36 500 days. The second line of the standard output should contain the number of cottages, living in which the professor can stay in Byteion for the amount of time specified in the first line. In the third line of the standard output your programme should write out the numbers of all such cottages, separated by single spaces, and arranged in increasing order. All cottages, which the professor can stay forever in, are considered equal.
Example
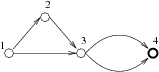
For the input data:3 5 1 2 1 3 2 3 3 4 3 4the correct outcome is: 4 1 1 |
|
3 5 1 2 2 3 3 1 3 4 3 4the correct outcome is:
zawsze 3 1 2 3

Print friendly version

