


| About Olympic -> Problems -> XIII OI 2005/2006 |  |

Task: Tetris 3D
Available memory: 128 MB
The authors of the game "Tetris" have decided to make a new, three-dimensional version, in which cuboids would fall down on a rectangular platform. The blocks fall down separately in a certain order, just like in the two-dimensional game. A block falls down until it reaches an obstacle: the platform or another block, that has already stopped - then it stops and remains in this exact position till the game is over.
However, the authors wanted to change the spirit of the game, turning it from a simple arcade-game into a play far more puzzling. Knowing the order of the falling blocks and their flight path the player's task is to tell the height of the heighest point of the arrangement after all blocks have fallen down (and stopped). All the blocks are falling down vertically and do not rotate while falling. For convenience we'll introduce a cartesian coordinate system on the platform, with the center in one of the platform's corners and the axes parallel to the platform's edges.
Write a programme that automates verification of the player's answer.
Task
Write a programme that:- reads the descriptions of subsequent falling blocks from the standard input,
- determines the height of the highest point of the arrangement of blocks after all have fallen down and stopped,
- writes the result to the standard output.
Input
In the first line of the input there are three integers D, S and N ( 1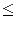 N
N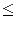 20 000,
1
20 000,
1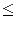 D, S
D, S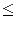 1 000),
separated by single spaces and denoting respectively:
the length and the depth of the platform and the number of blocks that are going to fall down on it.
In the following N lines the descriptions of subsequent blocks are given, one in each line.
1 000),
separated by single spaces and denoting respectively:
the length and the depth of the platform and the number of blocks that are going to fall down on it.
In the following N lines the descriptions of subsequent blocks are given, one in each line.
Each description of a block consists of five integers:
d, s, w, x and y
(1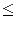 d, 0
d, 0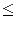 x, d + x
x, d + x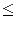 D,
1
D,
1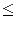 s, 0
s, 0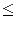 y, s + y
y, s + y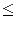 S,
1
S,
1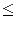 w
w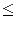 100 000),
representing a block of length d
depth s and height w
This very block will be be falling down on the platform with its d×s face as the bottom,
where the length and depth of the block are parallel to those of the platform.
The coordinates of the vertices of the projection of the block on the platform are:
(x, y), (x + d, y), (x, y + s) and (x + d, y + s).
100 000),
representing a block of length d
depth s and height w
This very block will be be falling down on the platform with its d×s face as the bottom,
where the length and depth of the block are parallel to those of the platform.
The coordinates of the vertices of the projection of the block on the platform are:
(x, y), (x + d, y), (x, y + s) and (x + d, y + s).
Output
The first and only line of the standard output should contain exactly one integer, the height of the highest point of the arrangement of blocks after all have fallen down ad stopped.
Example
For the following input data:7 5 4 4 3 2 0 0 3 3 1 3 0 7 1 2 0 3 2 3 3 2 2the correct answer is:
6

Print friendly version

