


| About Olympic -> Problems -> XIII OI 2005/2006 |  |

Task: Frogs
Available memory: 64 MBA scourge of frogs destroying all the crop has started in Byteotia. A farmer named Byteasar has decided to fight the vermin with peculiar "scarefrogs", that he has set up at certain points of his field. While moving from one place to another, every frog tries to keep as far of them as possible, i.e. maximizes the distance to the closest scarefrog.
The field that belongs to Byteasar has rectangular shape. The frogs leap in directions parallel to the field's sides and their leaps are unitary (of length 1). The scarefrogs-distance, for a given frog's route, is the minimum of all distances from all scarefrogs at all inter-leap-points of the route.
Byteasar already knows the most common starting and destination points of the frogs' routes, therefore he experiments with various deployments of the scarefrogs. He asks you for help, namely he would like you to write a programme that calculates the maximum (over all routes) scarefrogs-distance for a given deployment of scarefrogs -- which we call in short the frogshold distance.
Task
Write a programme that:- reads from the standard input the size of the field, the coordinates of the screfrogs and the source and target position of a frog,
- determines the frogshold distance (the maximum scarefrogs-distance a frog may achieve while still being able to reach the target point)
- writes the square of this number to the standard output.
Input
The first line of the input contains two integers: wx and wy separated by a single space -- the breadth and length of the field ( 2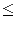 wx, wy
wx, wy 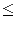 1 000).
The second line of the input contains four integers:
px, py, kx and ky separated by single spaces;
(px, py) is the initial position of the frog,
(kx, ky) is the target (final) position of the frog
(
1
1 000).
The second line of the input contains four integers:
px, py, kx and ky separated by single spaces;
(px, py) is the initial position of the frog,
(kx, ky) is the target (final) position of the frog
(
1 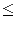 px, kx
px, kx 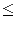 wx,
1
wx,
1 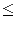 py, ky
py, ky 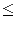 wy).
The third line of the stanard input contains one integer
n -- the number of scarefrogs deployed on the field
(
1
wy).
The third line of the stanard input contains one integer
n -- the number of scarefrogs deployed on the field
(
1 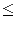 n
n 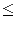 wx . wy).
The following n lines contain the coordinates of subsequent scarefrogs.
The line no. i + 3 for
1
wx . wy).
The following n lines contain the coordinates of subsequent scarefrogs.
The line no. i + 3 for
1 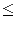 i
i 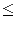 n contains two integers xi and yi separated
by a single space -- these are the coordinates of the ith scarefrog
(
1
n contains two integers xi and yi separated
by a single space -- these are the coordinates of the ith scarefrog
(
1 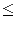 xi
xi 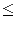 wx,
1
wx,
1 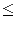 yi
yi 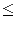 wy).
No two scarefrogs occupy the same position and none of them is at the point
(px, py) nor
(kx, ky).
wy).
No two scarefrogs occupy the same position and none of them is at the point
(px, py) nor
(kx, ky).
Output
In the first and only line of the standard output one integer should be written, namely the square of the frogshold distance. If the frog cannot avoid leaping directly on some scarefrog the result is 0.
Example
For the following input data:5 5 1 1 5 5 2 3 3 4 2the correct answer is:
4

Optimal route of the frog.

Print friendly version

