


| O olimpiadzie |  |

|
XI Olimpiada Informatyczna 2003/2004
|
| Zawody I stopnia |
| Plik źródłowy: | szn.xxx (xxx=pas,c,cpp) |
| Limit pamięci: | 32 MB |
Przedsiębiorstwo String-Toys S.A. zwróciło się do Ciebie o pomoc w rozwiązaniu następującego problemu. String-Toys S.A. chce produkować ze sznurka modele spójnych grafów acyklicznych.
Każdy graf składa się z wierzchołków i pewnej liczby krawędzi łączących różne wierzchołki. Ten sam wierzchołek może być połączony z wieloma innymi wierzchołkami. Graf jest spójny i acykliczny, gdy od każdego wierzchołka można przejść do każdego innego wierzchołka wędrując po krawędziach i co więcej, bez zawracania można to zrobić dokładnie na jeden sposób.
Wierzchołki grafów mają być modelowane przez węzły zawiązane na kawałkach sznurka, a krawędzie przez odcinki sznurka pomiędzy węzłami. Każdy węzeł może być wynikiem zasuplenia kawałka sznurka lub związania w tym samym miejscu wielu kawałków. Ze względów technicznych koszty produkcji zależą od liczby kawałków sznurka użytych do wykonania modelu, oraz od długości najdłuższego z kawałków. (Każda krawędź ma długość 1. Długość sznurka użytego do zrobienia węzłów jest pomijalna.)
Zadanie
Zadanie polega na napisaniu programu, który:
- wczyta ze standardowego wejścia opis spójnego grafu acyklicznego, który ma być modelowany,
- obliczy:
- minimalną liczbę kawałków sznurka potrzebnych do wykonania modelu,
- zakładając, że liczba kawałków sznurka jest minimalna, minimalną długość najdłuższego kawałka sznurka potrzebnego do wykonania modelu.
- wypisze dwie obliczone liczby na standardowe wyjście.
Wejście
Pierwszy wiersz zawiera jedną dodatnią liczbę całkowitą n - liczbę wierzchołków w grafie, 2 <= n <= 10 000. Wierzchołki są ponumerowane od 1 do n. Kolejne n - 1 wierszy zawiera opisy krawędzi, po jednej w wierszu. Każdy z tych wierszy zawiera parę liczb całkowitych a i b oddzielonych pojedynczym odstępem, 1 <= a, b <= n, a <> b. Para taka reprezentuje krawędź łączącą wierzchołki a i b.
Wyjście
Twój program powinien wypisać w pierwszym wierszu wyjścia dwie liczby całkowite k i l oddzielone pojedynczym odstępem: k powinno być minimalną liczbą kawałków sznurka potrzebnych do wykonania modelu grafu, a l powinno być minimalną długością najdłuższego kawałka sznurka (zakładając, że zużyliśmy k kawałków sznurka).
Przykład
Dla danych wejściowych:
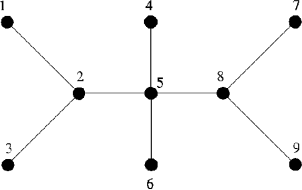
9 7 8 4 5 5 6 1 2 3 2 9 8 2 5 5 8
poprawnym wynikiem jest:
4 2

Wersja do druku