Olimpiada Informatyczna

Ten dokument nie jest dostępny w polskiej wersji językowej.
Niebieskie ksi.eczki

II Olympiad in Informatics 1994/1995

Task: DRZ

Author: Krzysztof Diks

Step Traversing a Tree

III stage contest

A graph is a pair (V, E), where V is a finite set of elements called vertices of the graph, and E is a subset of the set of all unordered pairs of distinct vertices. The elements of the set E are called edges of the graph. If for each pair of distinct vertices u, v there exists exactly one sequence of distinct vertices w₀, w₁, ..., w_k, such that w₀ = u, w_k = v and the pairs {w_i, w_i + 1} are in E, for i = 0, ..., k - 1, then the graph is called a tree. We say that the distance between the vertices u and v in the tree is k.

It is known that a tree of n vertices has exactly n - 1 edges. A tree T whose vertices are numbered from 1 to n can be unambiguously described by giving the number of its vertices n, and an appropriate sequence of n - 1 pairs of positive integers describing its edges.

Any permutation of vertices - i.e. a sequence in which each vertex appears exactly once - is called a traversing order of a tree. If the distance of each two consecutive vertices in some order of the tree T is at most c, then we say that it is a traversing order of the tree with step c.

It is known that for each tree its traversing order with step 3 can be found.

Example

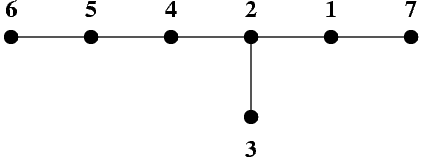
The picture shows a tree of 7 vertices. The vertices are represented by black dots, and edges by line segments joining the dots.

a tree

This tree can be traversed with step 3 by visiting its vertices in the following order: 7 2 3 5 6 4 1.

Task

Write a program that:

reads a description of a tree from the text file DRZ.IN,
finds an arbitrary traversing order of that tree with step 3,
writes that order in the text file DRZ.OUT.

Input

In the first line of the file DRZ.IN there is a positive integer n, not greater than 5000 - it is the number of vertices of the tree.
In each of the following n - 1 lines there is one pair of positive integers separated by a single space and representing one edge of the tree.

Output

In the successive lines of the file DRZ.OUT one should write the numbers of the successive vertices in a traversing order of the tree with step 3 - each number should be written in a separate line.

Example

The following file DRZ.IN is a correct description of the tree presented in the picture:

The following file DRZ.OUT is a correct solution:

Your program should look for the file DRZ.IN in the current directory and create the file DRZ.OUT also in the current directory. The source file containing the program written by you should be named DRZ.???, where ??? are substituted by at most three-letter abbreviation of the programming language used. The same program in an executable form should be written in a file DRZ.EXE.