


| O olimpiadzie -> Zadania -> XI OI 2003/2004 |  |

|
XI Olimpiada Informatyczna 2003/2004
|
| Zawody I stopnia |
| Plik źródłowy: | gra.xxx (xxx=pas,c,cpp) |
| Limit pamięci: | 32 MB |
Rozważmy grę na prostokątnej planszy m x 1 złożonej z m jednostkowych kwadratów ponumerowanych kolejno od l do m. Na planszy ustawionych jest n pionków, każdy na innym polu, przy czym żaden pionek nie znajduje się na polu o numerze m. Pojedynczy ruch w grze polega na przestawieniu dowolnie wybranego pionka na pierwsze wolne pole o większym numerze. Dwaj gracze wykonują na zmianę po jednym ruchu. Wygrywa ten, który postawi pionek na ostatnim polu, tzn. na polu o numerze m.
Dla przykładu z rysunku (m = 7), gracz może wykonać ruch z pola 2 na 4, z pola 3 na 4 lub z pola 6 na 7. Ten ostatni ruch kończy grę.
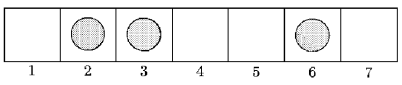
Mówimy, że ruch gracza jest wygrywający, jeżeli po jego wykonaniu gracz ten może wygrać grę niezależnie od tego, jakie ruchy będzie wykonywał jego przeciwnik.
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia rozmiar planszy i początkowe rozstawienie pionków,
- wyznaczy liczbę różnych ruchów wygrywających, jakie w zadanej sytuacji początkowej ma do wyboru gracz rozpoczynający grę,
- wypisze wynik na standardowe wyjście.
Wejście
Pierwszy wiersz wejścia zawiera dwie liczby całkowite m i n (2 <= m <= 109, 1 <= n <= 106, n < m) oddzielone pojedynczym odstępem. Drugi wiersz zawiera n rosnących numerów pól, na których znajdują się pionki. Liczby w wierszu są pooddzielane pojedynczymi odstępami.
Wyjście
Pierwszy i jedyny wiersz wyjścia powinien zawierać liczbę różnych ruchów wygrywających, jakie może wykonać w zadanej sytuacji początkowej gracz rozpoczynający grę.
Przykład
Dla danych wejściowych:
5 2 1 3
prawidłową odpowiedzią jest:
1
Dla danych wejściowych:
5 2 2 3
prawidłową odpowiedzią jest:
0

Wersja do druku

