


| Historia OI -> XII OI 2004/2005 -> Zadania |  |

|
XII Olimpiada Informatyczna 2004/2005
|
| Zawody I stopnia |
| Plik źródłowy: | pun.xxx (xxx=pas,c,cpp) |
| Limit pamięci: | 32 MB |
Alternatywne formaty: PostScript | PDF
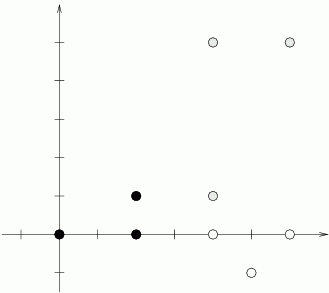
Dany jest zbiór punktów na płaszczyźnie o współrzędnych całkowitych, który będziemy nazywać wzorem, oraz zestaw innych zbiorów punktów na płaszczyźnie (również o współrzędnych całkowitych). Interesuje nas, które z podanych zestawów są podobne do wzoru, tzn. czy można je tak przekształcić za pomocą obrotów, przesunięć, symetrii osiowej i jednokładności, aby były identyczne ze wzorem. Przykładowo: zbiór punktów {(0,0), (2,0), (2,1)} jest podobny do zbioru {(6,1), (6,5), (4,5)}, ale nie do zbioru {(4,0), (6,0), (5,-1)}.
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia opisy: wzoru oraz zestawu badanych zbiorów punktów,
- wyznaczy, które z badanych zbiorów punktów są podobne do wzoru,
- wypisze wynik na standardowe wyjście.
Wejście
W pierwszym wierszu standardowego wejścia zapisana jest jedna liczba całkowita k (1 <= k <= 25.000) - liczba punktów tworzących wzór. W kolejnych k wierszach zapisane są pary liczb całkowitych pooddzielanych pojedynczymi odstępami. W i+1-ym wierszu są współrzędne i-tego punktu należącego do wzoru: x_i i y_i (-20.000 <= x_i, y_i <= 20.000). Punkty tworzące wzór są (parami) różne. W kolejnym wierszu zapisana jest liczba zbiorów do zbadania n (1 <= n <= 20). Dalej następuje n opisów zbiorów punktów. Opis każdego zbioru rozpoczyna się od wiersza zawierającego jedną liczbę całkowitą l - liczbę punktów w danym zbiorze (1 <= l <= 25.000). Punkty te są opisane w kolejnych wierszach, po jednym w wierszu. Opis punktu to dwie liczby całkowite oddzielone pojedynczym odstępem, jego współrzędne x i y (-20.000 <= x, y <= 20.000). Punkty tworzące jeden zbiór są parami różne.
Wyjście
Twój program powinien wypisać na standardowe wyjście n wierszy - po jednym dla każdego badanego zbioru punktów. Wiersz nr i powinien zawierać słowo TAK, gdy i-ty z podanych zbiorów punktów jest podobny do podanego wzoru, lub słowo NIE w przeciwnym przypadku.
Przykład
Dla danych wejściowych:
3 0 0 2 0 2 1 2 3 4 1 6 5 4 5 3 4 0 6 0 5 -1
prawidłową odpowiedzią jest:
TAK NIE

Wersja do druku

