


| Historia OI -> XI OI 2003/2004 |  |

|
XI Olimpiada Informatyczna 2003/2004
|
| Zawody III stopnia |
| Plik źródłowy: | kag.* |
| Limit pamięci: | 32 MB |
Kaglony to narodowa ulubiona potrawa mieszkańców Bajtocji. Kaglony mają bardzo charakterystyczną budowę. Glon składający się z jednej komórki jest kaglonem. Mając dwa kaglony K1 i K2, można je połączyć w następujący sposób:
-
biorąc wszystkie komórki z K1 i K2, oraz wszystkie połączenia
z K1 i K2,

-
biorąc wszystkie komórki z K1 i K2, wszystkie połączenia
z K1 i K2, oraz dodając nowe połączenia:
każdą komórkę z K1 łączymy z każdą komórką z K2.
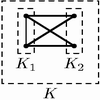
Niestety niedawno wrogie państwo Bitocji rozpoczęło sprzedaż glonów imitujących kaglony. Glony te są na tyle podobne że na pierwszy rzut oka trudno odróżnić je od oryginału, dlatego też rząd Bajtocji poprosił Cię o napisanie programu, który umożliwiłby sprawdzanie czy dany glon jest kaglonem.
Zadanie
Napisz program który:
- wczyta ze standardowego wejścia opisy glonów,
- sprawdzi które z nich są poprawnymi kaglonami,
- zapisze na standardowym wyjściu odpowiedź.
Wejście
W pierwszym wierszu standardowego wejścia zapisana jest jedna liczba całkowita k, 1 <= k <= 10, liczba badanych glonów. W kolejnych wierszach zapisane jest k opisów glonów. Pojedynczy opis ma następującą postać: w pierwszym wierszu zapisane są dwie liczby całkowite oddzielone pojedynczym odstępem n i m, 1 <= n <= 10.000, 0 <= m <= 100.000, odpowiednio liczba komórek i liczba połączeń. Komórki są ponumerowane od 1 do n. W kolejnych m wierszach opisane są połączenia, w każdym z tych wierszy zapisano dwie liczby całkowite oddzielone pojedynczym odstępem a, b, a<>b, 1 <= a,b <= n, oznaczające, że komórki a i b są połączone. Każde połączenie wymienione jest jeden raz.
Wyjście
Na standardowym wyjściu należy zapisać k wierszy. W i-tym wierszy należy zapisać jedno słowo:
- TAK - jeśli i-ty glon jest poprawnym kaglonem,
- NIE - wpp.

Wersja do druku

