


| Historia OI -> IX OI 2001/2002 -> Zadania |  |

|
IX Olimpiada Informatyczna 2001/2002
|
|
Zadanie: izo
|
Autor: Zbigniew Czech
|
| Zawody II stopnia, dzień próbny |
| Plik źródłowy: | izo.??? (np. pas, c, cpp) |
| Plik wejściowy: | izo.in |
| Plik wyjściowy: | izo.out |
Firma Izomax produkuje wielowarstwowe izolatory cieplne. Każda z i warstw, i=1, 2, ..., n, cechuje się dodatnim współczynnikiem izolacji ai. Warstwy są ponumerowane zgodnie z kierunkiem ucieczki ciepła.
ciepło -> || a1 | a2 | ... | ai | ai+1 | ... | an || ->
Współczynnik izolacji całego izolatora, A, określony jest sumą współczynników izolacji jego warstw. Ponadto współczynnik A rośnie, jeśli po warstwie o niższym współczynniku izolacji występuje warstwa o wyższym współczynniku, zgodnie z wzorem:
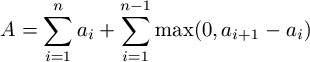
Na przykład, współczynnik izolacji izolatora o postaci:
-> || 5 | 4 | 1 | 7 || ->
wynosi A = (5+4+1+7)+(7-1) = 23.
Zadanie
Napisz program, który dla zadanych współczynników izolacji warstw a1, a2, ..., an wyznacza taką kolejność warstw, dla której współczynnik izolacji A całego izolatora jest największy.
Wejście
W pierwszym wierszu pliku tekstowego izo.in zapisana jest liczba warstw n, 1 <= n <= 100000. W kolejnych n wierszach zapisane są współczynniki a1, a2, ..., an, po jednym w każdym wierszu. Współczynniki te są liczbami całkowitymi i spełniają nierówności 1 <= ai <= 10000.
Wyjście
W pierwszym i jedynym wierszu pliku tekstowego izo.out. Twój program powinien zapisać jedną liczbę całkowitą równą największej możliwej wartości współczynnika izolacji A izolatora zbudowanego z warstw o podanych współczynnikach, ułożonych w odpowiedniej kolejności.
Przykład
Dla pliku wejściowego izo.in:
4 5 4 1 7poprawną odpowiedzią jest plik wyjściowy izo.out:
24

