


| Historia OI -> VI OI 1998/1999 -> Zadania |  |

|
VI Olimpiada Informatyczna 1998/99
|
|
Zadanie: LUN
|
Autor: Wojciech Rytter
|
| Zawody II stopnia, dzień pierwszy | 10 lutego 1999 |
| Plik źródłowy: | LUN.??? (np. pas, c, cpp) |
| Plik wykonywalny: | LUN.exe |
| Plik wejściowy: | LUN.in |
| Plik wyjściowy: | LUN.out |
Płaski dach budynku ma kształt kwadratu o rozmiarach 3k, 3k i bokach równoległych do kierunków północ-południe oraz wschód-zachód. Dach pokryto kwadratowymi kaflami o boku 1, ale jeden kafel został wyrwany i w tym miejscu jest dziura. Kafle na dachu tworzą prostokątną siatkę, wobec tego ich pozycje można określić za pomocą współrzędnych. Kafel położony w południowo-zachodnim rogu ma współrzędne (1,1). Pierwsza współrzędna rośnie przy przemieszczaniu się na wschód, a druga przy przemieszczaniu się na północ.
Lunatyk przemierza dach przemieszczając się w każdym kroku z kafla, na którym aktualnie się znajduje, na kafel sąsiedni od wschodu (E), zachodu (W), południa (S) lub północy (N). Wędrówka lunatyka po dachu zaczyna się zawsze od kafla w rogu południowo-zachodnim, a opisem drogi jest słowo dk złożone z liter N, S, E, W oznaczających, odpowiednio, krok na północ, na południe, na wschód i na zachód. Dla k = 1 opisem drogi lunatyka jest słowo
Dla k = 2 opisem drogi lunatyka jest słowo
| d2 | = |
NNEESWSEENNEESWSEEEENNWSWNNEENNWSW - NNEENNWSWNWWWSSENESSSSWWNENWWSSW - WNENWNEENNWSWN. |
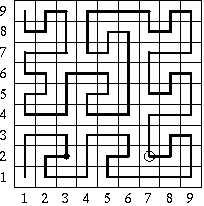
Spójrz na rysunek przedstawiający drogi lunatyka po dachach o rozmiarach 3*3 i 9*9. Ogólnie, dla dowolnego k>=1, opisem drogi lunatyka po dachu o rozmiarach 3k+1*3k+1 jest słowo:
| a: | E->N | W->S | N->E | S->W |
| b: | E->S | W->N | N->W | S->E |
| c: | E->W | W->E | N->S | S->N |
np. a(SEN)=WNE, b(SEN)=ESW, c(SEN)=NWS.
Zaczynamy obserwować lunatyka w momencie, gdy znajduje się na
kaflu o współrzędnych (u 1,u 2). Po ilu krokach lunatyk wpadnie do
dziury, która znajduje się w kwadracie o współrzędnych (v 1,v 2)?
Przykład
Na rysunku przedstawiono drogi lunatyka po dachu o rozmiarach 3*3 oraz po dachu o rozmiarach 9*9. W drugim przypadku zaznaczono punkt, od którego rozpoczynamy obserwację lunatyka i dziurę w dachu. Lunatyka dzieli od dziury 20 kroków.
 |
 |
Zadanie
Napisz program, który:
- wczytuje z pliku tekstowego LUN.IN liczbę naturalną k określającą rozmiary dachu (3k*3k), pozycję lunatyka w chwili, gdy rozpoczynamy jego obserwację oraz pozycję dziury,
- oblicza liczbę kroków, które dzielą lunatyka od dziury,
- zapisuje wynik w pliku tekstowym .
Wejście
W pierwszym wierszu pliku tekstowego LUN.IN jest zapisana jedna liczba naturalna k, 1<=k<=60, określająca rozmiary dachu (3k*3k). W każdym z kolejnych dwóch wierszy pliku LUN.IN są zapisane dwie liczby naturalne x, y oddzielone odstępem, 1<=x<=3^k, 1<=y<=3^k. Liczby w drugim wierszu pliku LUN.IN są współrzędnymi kafla, na którym stoi lunatyk; liczby w trzecim wierszu pliku LUN.IN są współrzędnymi dziury. Możesz założyć, że dane są tak dobrane, iż po pewnej liczbie kroków lunatyk wpadnie do dziury.
Wyjście
Jedyny wiersz pliku wyjściowego LUN.OUT powinien zawierać liczbę kroków, które dzielą lunatyka od dziury.
Przykład
Dla pliku wejściowego LUN.IN2 3 2 7 2poprawną odpowiedzią jest plik tekstowy LUN.OUT
20

