


| Historia OI -> II OI 1994/1995 |  |

|
II Olimpiada Informatyczna 1994/95
|
|
Zadanie: DRZ
|
Autor: Wojciech Rytter
|
| Zawody I stopnia |
| Plik źródłowy: | DRZ.??? (np. pas, c, cpp) |
| Plik wykonywalny: | DRZ.exe |
| Plik wejściowy: | DRZ.in |
| Plik wyjściowy: | DRZ.out |
Drzewa występują bardzo często w informatyce. W odróżnieniu od drzew w naturze drzewa w informatyce rosną do góry nogami: korzeń jest na górze, a liście są na dole. Drzewo składa się z elementów zwanych węzłami. Jeden z węzłów jest korzeniem. Każdy węzeł w (oprócz korzenia) ma swojego (dokładnie jednego) ojca v. Jeśli węzeł v jest ojcem w, to w jest synem v. Węzły nie mające synów nazywamy liśćmi. Synów węzła w, ich synów, synów ich synów itd. nazywamy potomkami węzła w. Każdy węzeł - oprócz korzenia - jest potomkiem korzenia. Każdy węzeł ma swój poziom. Korzeń ma poziom 0, a synowie mają poziom o jeden większy od swoich ojców.
Drzewo jest pełnym drzewem binarnym wtedy i tylko wtedy, gdy każdy węzeł ma dokładnie dwóch lub zero synów. W drzewach binarnych rozróżniamy lewego i prawego syna.
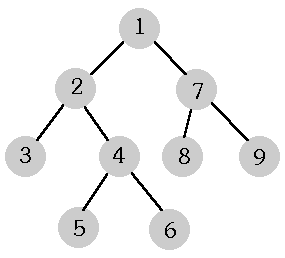
Powyższy rysunek przedstawia przykładowe pełne drzewo binarne. Węzły tego drzewa są ponumerowane w specjalnej kolejności (nazywanej w literaturze angielskiej preorder). W kolejności tej korzeń ma numer 1, ojciec poprzedza synów, a lewy syn i dowolny jego potomek ma numer mniejszy niż prawy syn i każdy jego potomek.
Jest wiele sposobów zapisu pełnych drzew binarnych z taką numeracją węzłów. Oto trzy z nich.
Zapis genealogiczny
Jest to ciąg liczb. Pierwszy element ciągu jest równy 0 (zero), zaś dla j > 1, j-ty wyraz ciągu jest numerem ojca węzła
j.
Zapis nawiasowy
Każdemu węzłowi przyporządkowujemy napis złożony z nawiasów. Liściom przyporządkowujemy napis ().
Każdemu z pozostałych węzłów w przyporządkowujemy napis postaci: (lp), gdzie l i p oznaczają napisy
przyporządkowane odpowiednio lewemu i prawemu synowi w. Napis przyporządkowany korzeniowi jest zapisem
nawiasowym drzewa.
Zapis poziomowy
Jest to ciąg poziomów kolejnych liści drzewa (zgodnie z przyjętą numeracją).
Drzewo przedstawione na rysunku można opisać następująco:
| Zapis genealogiczny | 0 1 2 2 4 4 1 7 7 |
| Zapis nawiasowy | ((()(()()))(()())) |
| Zapis poziomowy | 2 3 3 2 2 |
Zadanie
Napisz program, który wczytuje z pliku tekstowego DRZ.IN ciąg liczb i bada, czy jest on zapisem poziomowym pełnego drzewa binarnego. Jeśli nie jest, to zapisuje w pliku tekstowym DRZ.OUT jeden wyraz NIE, a jeśli jest, to znajduje dwa inne zapisy tego drzewa (genealogiczny i nawiasowy) i zapisuje je w pliku tekstowym DRZ.OUT.
Wejście
W pierwszym wierszu pliku DRZ.IN zapisana jest dodatnia liczba wyrazów ciągu (nie większa niż 2500). W drugim wierszu zapisane są kolejne wyrazy ciągu oddzielone pojedynczymi odstępami. Liczby w pliku DRZ.IN są zapisane poprawnie. Twój program nie musi tego sprawdzać.
Wyjście
Plik DRZ.OUT powinien zawierać- tylko jeden wyraz NIE
- albo:
- w pierwszym wierszu kolejne wyrazy zapisu genealogicznego oddzielone pojedynczymi odstępami,
- w drugim wierszu zapis nawiasowy, tzn. ciąg nawiasów lewych i prawych bez odstępów między nimi.
Przykłady
Dla pliku DRZ.IN:5
2 2 3 3 2
Twój program powinien utworzyć następujący plik DRZ.OUT:
0 1 2 2 1 5 6 6 5
((()())((()())()))
Dla pliku DRZ.IN:
4
1 2 2 3
Twój program powinien utworzyć plik DRZ.OUT:
NIE
Twój program powinien szukać pliku DRZ.IN w katalogu bieżącym i tworzyć plik DRZ.OUT również w bieżącym katalogu. Plik zawierający napisany przez Ciebie program w postaci źródłowej powinien mieć nazwę DRZ.???, gdzie zamiast ??? należy wpisać co najwyżej trzyliterowy skrót nazwy użytego języka programowania. Ten sam program w postaci wykonywalnej powinien być zapisany w pliku DRZ.EXE.

