Marcin Kubica (treść, opracowanie) Krzysztof Sobusiak (program wzorcowy)
Labirynt studni
Wewnątrz Bajtogóry znajduje się mityczny labirynt studni. Wejście do labiryntu znajduje się na szczycie góry. Labirynt składa się z wielu komnat. Każda z nich jest w jednym z trzech kolorów: czerwonym, zielonym lub niebieskim. Dwie komnaty tego samego koloru wyglądają identycznie i są nieodróżnialne. W każdej komnacie znajdują się trzy studnie oznaczone numerami 1, 2 i 3. Między komnatami można poruszać się tylko w jeden sposób - wskakując do jednej ze studni spada się (niekoniecznie pionowo) do jednej z komnat położonych niżej. Z komnaty, w której znajduje się wejście do labiryntu można przedostać się w ten sposób do każdej z pozostałych komnat. Wszystkie drogi przez labirynt prowadzą do smoczej jamy znajdującej się na samym jego dnie. Każdemu przejściu przez labirynt odpowiada ciąg numerów studni wybieranych w kolejno odwiedzanych komnatach. Ciąg ten nazywa się planem podróży.
W smoczej jamie żyje Bajtosmok. Legenda głosi, że ten, kto przedstawi Bajtosmokowi dokładny plan labiryntu, otrzyma wielkie skarby. Wszystkich innych Bajtosmok potężnym kopnięciem wyprasza z wnętrza góry.
Śmiałek o imieniu Bajtazar wielokrotnie przemierzał labirynt i opracował jego mapę. Jednak Bajtosmok orzekł, że co prawda wszystkie komnaty znajdują się na mapie, ale wiele komnat jest na niej powtórzonych.
- Ja też - powiedział poklepując Bajtazara po ramieniu - projektując labirynt narysowałem podobny rysunek, ale szybko stwierdziłem, że komnat można zrobić o wiele mniej, a gość poruszający się według dowolnego planu podróży i tak będzie oglądał takie same sekwencje komnat. Pomyślałem trochę i maksymalnie zredukowałem projekt.
Zadanie
Napisz program, który:
- wczyta mapę Bajtazara z pliku tekstowego LAB.IN,
- obliczy prawdziwą liczbę komnat w labiryncie,
- zapisze wynik do pliku tekstowego LAB.OUT.
Wejście
W pierwszym wierszu pliku tekstowego LAB.IN zapisana jest jedna liczba całkowita n, 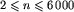 , będąca liczbą komnat (łącznie ze smoczą jamą). Komnaty są ponumerowane od 1 do n tak, że komnaty o większych numerach znajdują się niżej (komnata, w której znajduje się wejście do labiryntu ma numer 1, a smocza jama ma numer n). W kolejnych n-1 wierszach pliku są opisane komnaty (poza smoczą jamą) oraz studnie prowadzące od nich w dół. W każdym z tych wierszy znajduje się litera, po niej jeden znak odstępu, a następnie trzy liczby całkowite oddzielone pojedynczymi odstępami. Litera oznacza kolor komnaty (C - czerwony, Z - zielony, N - niebieski), a i-ta liczba (dla i = 1, 2, 3) jest numerem komnaty, do której prowadzi i-ta studnia.
, będąca liczbą komnat (łącznie ze smoczą jamą). Komnaty są ponumerowane od 1 do n tak, że komnaty o większych numerach znajdują się niżej (komnata, w której znajduje się wejście do labiryntu ma numer 1, a smocza jama ma numer n). W kolejnych n-1 wierszach pliku są opisane komnaty (poza smoczą jamą) oraz studnie prowadzące od nich w dół. W każdym z tych wierszy znajduje się litera, po niej jeden znak odstępu, a następnie trzy liczby całkowite oddzielone pojedynczymi odstępami. Litera oznacza kolor komnaty (C - czerwony, Z - zielony, N - niebieski), a i-ta liczba (dla i = 1, 2, 3) jest numerem komnaty, do której prowadzi i-ta studnia.
Wyjście
W pierwszym i jedynym wierszu pliku tekstowego LAB.OUT powinna znaleźć się dokładnie jedna liczba całkowita będąca minimalną liczbą komnat w labiryncie (łącznie ze smoczą jamą), przy której podróżnik poruszający się według dowolnego planu obserwuje taką samą sekwencję komnat, jak dla labiryntu opisanego w pliku wejściowym.
Przykład
Dla pliku wejściowego LAB.IN:
11
N 3 5 2
Z 4 5 6
N 7 11 9
N 8 11 10
C 11 9 9
Z 11 9 10
C 11 11 11
C 11 11 11
Z 11 11 11
Z 11 11 11
opisującego następujący labirynt: 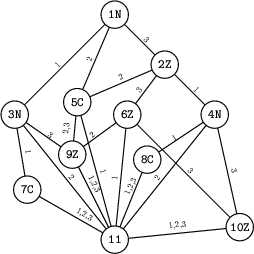 poprawną odpowiedzią jest plik tekstowy LAB.OUT:
poprawną odpowiedzią jest plik tekstowy LAB.OUT:
8
Rozwiązanie
Sformułujmy to zadanie w terminologii grafowej. Plan labiryntu to multigraf(Multigraf różni się tym od grafu, że może mieć wiele krawędzi łączących tę samą parę wierzchołków.) skierowany bez cykli - jego wierzchołki reprezentują komnaty, a krawędzie reprezentują studnie. Każdy wierzchołek (z wyjątkiem smoczej jamy) jest pokolorowany jednym z trzech kolorów: czerwonym, zielonym lub niebieskim. Z każdego wierzchołka wychodzą po trzy krawędzie etykietowane liczbami 1, 2 i 3, z wyjątkiem smoczej jamy, z której nie wychodzą żadne krawędzie. Dla każdego wierzchołka na planie istnieje ścieżka prowadząca do niego z wierzchołka reprezentującego wejście do labiryntu. Podobnie, dla każdego wierzchołka istnieje ścieżka prowadząca z niego do smoczej jamy.
Każdej ścieżce prowadzącej z wejścia do labiryntu do smoczej jamy odpowiada plan podróży, będący ciągiem etykiet krawędzi tworzących daną ścieżkę, oraz ciąg kolorów wierzchołków tworzących tę ścieżkę. Równocześnie plan podróży wyznacza jednoznacznie odpowiadającą mu ścieżkę łączącą wejście do labiryntu ze smoczą jamą. Możemy powiedzieć, że dwa plany labiryntów są sobie równoważne, jeżeli:
- mają one takie same zbiory możliwych planów podróży, oraz
- dla każdego z tych planów podróży, odpowiadające im w obu multigrafach ścieżki łączące wejścia do labiryntów ze smoczymi jamami, charakteryzują się takimi samymi sekwencjami kolorów wierzchołków.
Zadanie polega na znalezieniu planu labiryntu o najmniejszej liczbie wierzchołków, równoważnego zadanemu planowi. Zastanówmy się, jak mógłby wyglądać taki minimalny plan.
Przez głębokość wierzchołka oznaczamy długość najdłuższej ścieżki prowadzącej z tego wierzchołka do smoczej jamy. Przyjmujemy, że smocza jama ma głębokość 0. Zbiór wszystkich wierzchołków o danej głębokości nazywamy warstwą.
Powiedzieliśmy, że każdej ścieżce łączącej wejście do labiryntu ze smoczą jamą odpowiada pewien plan podróży i jednocześnie ten plan podróży jednoznacznie wyznacza tę ścieżkę. Fakt ten można uogólnić. Każdej ścieżce możemy przyporządkować jej "plan" będący ciągiem etykiet krawędzi tworzących tę ścieżkę. Równocześnie taki plan, wraz z początkowym wierzchołkiem, wyznacza jednoznacznie tę ścieżkę.
Charakterystyką ścieżki będziemy nazywać parę złożoną z planu ścieżki oraz ciągu kolorów wierzchołków tworzących tę ścieżkę. Dla każdego wierzchołka definiujemy jego charakterystykę, jako zbiór charakterystyk wszystkich ścieżek prowadzących z tego wierzchołka do smoczej jamy.
Zauważmy, że wierzchołki mające taką samą charakterystykę należą do tej samej warstwy. Ponadto, jeśli z wierzchołków o takiej samej charakterystyce przejdziemy równocześnie wzdłuż krawędzi o takiej samej etykiecie, to dojdziemy do wierzchołków o takiej samej charakterystyce. Tak więc, w szukanym planie nie może być dwóch wierzchołków o takiej samej charakterystyce - gdyby były, to moglibyśmy skleić ze sobą dwa wierzchołki o takiej samej charakterystyce i minimalnej głębokości, uzyskując plan labiryntu równoważny danemu, ale o mniejszej liczbie wierzchołków. Ponadto, dla dowolnego wierzchołka v w danym planie labiryntu i dla dowolnej ścieżki prowadzącej od wejścia do labiryntu do v, w szukanym planie istnieje ścieżka o takiej samej charakterystyce, prowadząca od wejścia do labiryntu do wierzchołka o takiej samej charakterystyce, jak charakterystyka v. Wynika stąd, że szukany plan labiryntu możemy uzyskać sklejając wierzchołki o takich samych charakterystykach.
Sklejając wierzchołki nie musimy wyznaczać ich charakterystyk. Możemy skorzystać z następującego prostego faktu. Niech v i w będą dwoma wierzchołkami o głębokości h. Jeżeli wszystkie wierzchołki o głębokościach mniejszych od h mają różne charakterystyki, to v i w mają takie same charakterystyki wtedy i tylko wtedy, gdy krawędzie o takich samych etykietach, wychodzące z v i w prowadzą do takich samych wierzchołków. Fakt ten wynika bezpośrednio z definicji charakterystyki. Tak więc, najlepiej sklejać wierzchołki o tych samych charakterystykach z kolejnych warstw o rosnących głębokościach.
Nasze rozwiązanie składa się z dwóch faz: podzielenia wierzchołków na warstwy i sklejania wierzchołków z kolejnych warstw. Jak jednak podzielić wierzchołki na warstwy? Możemy posłużyć się tu algorytmem podobnym do sortowania topologicznego. Warstwy wyznaczamy w kolejności rosnących głębokości. W momencie, gdy wstawiamy jakiś wierzchołek do warstwy, to "przeglądamy" wszystkie krawędzie wchodzące do tego wierzchołka. Jeżeli wszystkie trzy krawędzie wychodzące z któregokolwiek wierzchołka zostaną przejrzane, to możemy wstawić ten wierzchołek do warstwy o głębokości o jeden większej od głębokości wierzchołka, do którego prowadzi ostatnia przejrzana krawędź.
Z każdym wierzchołkiem możemy mieć związany licznik, który początkowo jest równy 3. Wówczas "przejrzenie" krawędzi polega na zmniejszeniu o 1 licznika związanego z wierzchołkiem, z którego dana krawędź wychodzi. Gdy licznik osiągnie 0, to wszystkie krawędzie wychodzące z danego wierzchołka zostały przejrzane.
Do zaimplementowania opisanego algorytmu może być przydatna następująca struktura danych. Dla każdego wierzchołka pamiętamy jego kolor, krawędzie wychodzące z tego wierzchołka, krawędzie wchodzące do tego wierzchołka oraz pewne dodatkowe informacje potrzebne w trakcie sklejania wierzchołków, które omówimy dalej.
| 1 | const MAXN = 6000; { Maksymalna liczba wierzchołków. } |
| 2 | type |
| 3 | PElem = ^TElem; { Listy nieujemnych liczb całkowitych. } |
| 4 | TElem = record |
| 5 | l: Word; |
| 6 | nast: PElem |
| 7 | end |
| 8 | TKolejka = record { Kolejki nieujemnych liczb całkowitych. } |
| 9 | pocz, kon: PElem |
| 10 | end |
| 11 | TListy = array [0..MAXN] of PElem; { Tablica list. } |
| 12 | TKolejki = array [1..MAXN] of TKolejka; { Tablica kolejek. } |
| 13 | var |
| 14 | n: Word; { Liczba wierzchołków. } |
| 15 | V: array [1..MAXN] of record { Wierzchołki. } |
| 16 | kolor: Byte; { Kolor. } |
| 17 | numer: Word; { Numeracja używana przy sklejaniu wierzchołków. } |
| 18 | dol: array [1..3] of Word { Krawędzie wychodzące z wierzchołków. } |
| 19 | end |
| 20 | Gora: ^TListy; { Krawędzie prowadzące do wierzchołków. } |
| 21 | Warstwy: ^TListy; { Warstwy o kolejnych głębokościach. } |
Zwróćmy uwagę, że ze względu na ograniczoną wielkość pojedynczej tablicy, dane o wierzchołkach są pamiętane w trzech tablicach.
Funkcja dzieląca wierzchołki na warstwy wygląda następująco:
| 1 | procedure Wstaw(var L: PElem; i: Word); |
| 2 | { Wstawia liczbę i na początek listy L. } |
| 3 | ... |
| 4 | |
| 5 | function WyznaczWarstwy: Word; |
| 6 | { Wyznacza warstwy, w wyniku daje liczbę warstw. } |
| 7 | var |
| 8 | i, gleb: Word; |
| 9 | P, Q: PElem; |
| 10 | T: array [0..MAXN] of Byte; { Liczby nieodwiedzonych krawędzi. } |
| 11 | begin |
| 12 | for i := 0 to n do begin |
| 13 | Warstwy^[i] := nil; |
| 14 | T[i] := 3 |
| 15 | end; |
| 16 | Wstaw(Warstwy^[0], n); |
| 17 | gleb := 0; { Głębokość aktualnie przetwarzanej warstwy. } |
| 18 | while Warstwy^[gleb] 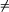 nil do begin nil do begin |
| 19 | { Wyznacz kolejne warstwy. } |
| 20 | P := Warstwy^[gleb]; |
| 21 | while 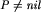 do begin do begin |
| 22 | { Przejrzyj wszystkie wierzchołki warstwy. } |
| 23 | i := P^.l; |
| 24 | Q := Gora^[i]; |
| 25 | while 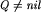 do begin do begin |
| 26 | { Przejrzyj wszystkie krawędzie wchodzące do danego } |
| 27 | { wierzchołka. } |
| 28 | Dec(T[Q^.l]); |
| 29 | if T[Q^.l] = 0 then |
| 30 | Wstaw(Warstwy^[gleb+1], Q^.l); |
| 31 | { Wierzchołek, z którego prowadzi krawędź, } |
| 32 | { należy do następnej warstwy. } |
| 33 | Q := Q^.nast |
| 34 | end; |
| 35 | P := P^.nast |
| 36 | end; |
| 37 | Inc(gleb) |
| 38 | end; |
| 39 | WyznaczWarstwy := gleb-1 |
| 40 | end; |
Każdy wierzchołek jest raz wstawiany do swojej warstwy i raz przeglądany. Każda krawędź jest przeglądana dokładnie raz. Tak więc złożoność czasowa pierwszej fazy algorytmu jest rzędu n, gdzie n jest liczbą wierzchołków.
Druga faza algorytmu polega na sklejaniu w kolejnych warstwach wierzchołków o takich samych charakterystykach. Każdemu wierzchołkowi możemy przyporządkować "kod" postaci 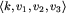 , gdzie k to kolor wierzchołka, a v_1, v_2, v_3, to wierzchołki, do których prowadzą krawędzie wychodzące z danego wierzchołka. Przetwarzając wierzchołki z kolejnej warstwy sklejamy wierzchołki o takich samych kodach. Jak jednak wyznaczyć, które wierzchołki mają takie same kody? Możemy skorzystać ze struktury słownikowej (dowolnego rodzaju, o dostępie w czasie logarytmicznym) - w momencie, gdy wstawiamy do struktury kod, który już w nim jest, to odpowiednie wierzchołki należy skleić. W ten sposób wyznaczenie wierzchołków do sklejenia wymaga czasu
, gdzie k to kolor wierzchołka, a v_1, v_2, v_3, to wierzchołki, do których prowadzą krawędzie wychodzące z danego wierzchołka. Przetwarzając wierzchołki z kolejnej warstwy sklejamy wierzchołki o takich samych kodach. Jak jednak wyznaczyć, które wierzchołki mają takie same kody? Możemy skorzystać ze struktury słownikowej (dowolnego rodzaju, o dostępie w czasie logarytmicznym) - w momencie, gdy wstawiamy do struktury kod, który już w nim jest, to odpowiednie wierzchołki należy skleić. W ten sposób wyznaczenie wierzchołków do sklejenia wymaga czasu 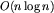 , gdzie n jest liczbą wierzchołków. Jeżeli zamiast słownika o dostępie w czasie logarytmicznym użyjemy tablicy haszującej, to możemy uzyskać oczekiwany czas O(n).
, gdzie n jest liczbą wierzchołków. Jeżeli zamiast słownika o dostępie w czasie logarytmicznym użyjemy tablicy haszującej, to możemy uzyskać oczekiwany czas O(n).
Można jednak wyznaczyć wierzchołki do sklejenia w pesymistycznym czasie 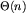 . Oznaczmy przez h głębokość wierzchołka z wejściem do labiryntu, przez ni oznaczmy liczbę wierzchołków w warstwie głębokości i. Zauważmy, że n_0 = n_h = 1 oraz
. Oznaczmy przez h głębokość wierzchołka z wejściem do labiryntu, przez ni oznaczmy liczbę wierzchołków w warstwie głębokości i. Zauważmy, że n_0 = n_h = 1 oraz 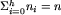 . W i-tym kroku drugiej fazy algorytmu sklejamy w i-tej warstwie wierzchołki o takich samych kodach. Z i-tej warstwy wychodzi 3ni krawędzi prowadzących do co najwyżej 3ni wierzchołków. Wierzchołki te możemy wyznaczyć i ponumerować w czasie rzędu ni. W kodach wierzchołków z i-tej warstwy wierzchołki, do których prowadzą krawędzie możemy reprezentować za pomocą numerów w tej numeracji. Wówczas możemy posortować kody leksykograficznie w czasie rzędu ni.
. W i-tym kroku drugiej fazy algorytmu sklejamy w i-tej warstwie wierzchołki o takich samych kodach. Z i-tej warstwy wychodzi 3ni krawędzi prowadzących do co najwyżej 3ni wierzchołków. Wierzchołki te możemy wyznaczyć i ponumerować w czasie rzędu ni. W kodach wierzchołków z i-tej warstwy wierzchołki, do których prowadzą krawędzie możemy reprezentować za pomocą numerów w tej numeracji. Wówczas możemy posortować kody leksykograficznie w czasie rzędu ni.
Oto fragment programu realizujący sortowanie kodów wierzchołków i-tej warstwy. Zakładamy, że początkowo wszystkie wierzchołki mają zainicjowane pola numer na 0, oraz że "kubły" są zainicjowane na puste kolejki.
| 1 | var num, i, j : Word; |
| 2 | P, Q, W: PElem; |
| 3 | Kubly : ^TKolejki; { Kubełki do sortowania leksykograficznego. } |
| 4 | |
| 5 | procedure Przerzuc(var K: TKolejka; var L: PElem); |
| 6 | { Przerzuca pierwszy element listy L na koniec kolejki K. } |
| 7 | ... |
| 8 | |
| 9 | function ScalKubly(maxnum: Word): PElem; |
| 10 | { Łączy kolejki z kubełków o numerach [1..maxnum] w jedną listę. } |
| 11 | ... |
| 12 | |
| 13 | begin |
| 14 | num := 0; |
| 15 | W := Warstwy[i]; |
| 16 | P := W; |
| 17 | while P 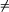 nil do begin nil do begin |
| 18 | { Ponumeruj wszystkie wierzchołki, do których prowadzą } |
| 19 | { krawędzie z i-tej warstwy. } |
| 20 | for j := 1 to 3 do with V[V[P^.l].Dol[j]] do |
| 21 | if numer = 0 then begin |
| 22 | Inc(num); |
| 23 | numer := num |
| 24 | end |
| 25 | P := P^.nast |
| 26 | end |
| 27 | { Sortuj leksykograficznie po numerach wierzchołków, } |
| 28 | { do których prowadzą krawędzie z i-tej warstwy. } |
| 29 | for j := 3 downto 1 do begin |
| 30 | while W 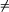 nil do nil do |
| 31 | Przerzuc(Kubly^[V[V[W^.l].Dol[j]].numer], W); |
| 32 | W := ScalKubly(num) |
| 33 | end |
| 34 | { Sortuj po kolorach wierzchołków. } |
| 35 | while W 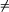 nil do nil do |
| 36 | Przerzuc(Kubly^[V[W^.l].kolor], W); |
| 37 | Warstwy[i] := ScalKubly(3); |
| 38 | end |
Po posortowaniu, takie same kody będą sąsiadować ze sobą - wystarczy więc przejrzeć je w kolejności posortowania i skleić wierzchołki o takich samych kodach.
Sklejając kilka wierzchołków, do wybranego wierzchołka doklejamy pozostałe. Doklejając jeden wierzchołek do drugiego musimy poprawić krawędzie prowadzące do pierwszego z nich - korzystamy tu z list wierzchołków, z których krawędzie prowadzą do danego wierzchołka. Możemy natomiast zaniedbać poprawianie list, na których występują sklejane wierzchołki, gdyż sklejamy wierzchołki w warstwach o coraz większych głębokościach i listy te nie będą już nam potrzebne. Oznaczmy przez wi liczbę krawędzi prowadzących do i-tej warstwy. Koszt czasowy sklejania wierzchołków z warstwy o głębokości i wynosi 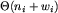 . Poniższy fragment kodu skleja odpowiednie wierzchołki.
. Poniższy fragment kodu skleja odpowiednie wierzchołki.
| 1 | function CzyZgodne(a, b: Word): Boolean; |
| 2 | { Sprawdza, czy a i b mają te same kody. } |
| 3 | var j: Word; |
| 4 | begin |
| 5 | CzyZgodne := False; |
| 6 | if V[a].kolor 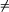 V[b].kolor { Muszą mieć ten sam kolor. } V[b].kolor { Muszą mieć ten sam kolor. } |
| 7 | then exit; |
| 8 | for j := 1 to 3 do |
| 9 | { Krawędzie muszą prowadzić do tych samych wierzchołków. } |
| 10 | if V[a].Dol[j] 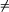 V[b].Dol[j] then exit; V[b].Dol[j] then exit; |
| 11 | CzyZgodne := True |
| 12 | end |
| 13 | |
| 14 | procedure LikwidujKomnate(a, b: Word); |
| 15 | { Dokleja wierzchołek b do a. } |
| 16 | var |
| 17 | P: PElem; j: Word; |
| 18 | begin |
| 19 | P := Gora^[b]; |
| 20 | while P 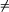 nil do begin nil do begin |
| 21 | with V[P^.l] do |
| 22 | for j := 1 to 3 do |
| 23 | if Dol[j] = b then Dol[j] := a; |
| 24 | P := P^.nast |
| 25 | end |
| 26 | end |
| 27 | |
| 28 | var |
| 29 | ile, a, b: Word; |
| 30 | P, Q, W: PElem; |
| 31 | begin |
| 32 | W := Warstwy[i]; P := W; Q := P^.nast; |
| 33 | ile := 1; {Liczba różnych wierzchołków warstwy.} |
| 34 | while Q 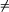 nil do begin {Przejdź posortowaną listę.} nil do begin {Przejdź posortowaną listę.} |
| 35 | a := P^.l; b := Q^.l; {Wierzchołki do ew. sklejenia.} |
| 36 | if CzyZgodne(a,b) then |
| 37 | LikwidujKomnate(a,b) |
| 38 | end begin {Wierzchołek istotnie różny od dotychczasowych.} |
| 39 | Inc(ile); |
| 40 | P := Q; |
| 41 | end |
| 42 | Q := Q^.nast |
| 43 | end |
| 44 | P := W; |
| 45 | while P 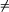 nil do begin {Likwiduj numerację.} nil do begin {Likwiduj numerację.} |
| 46 | for j := 1 to 3 do |
| 47 | V[V[P^.l].Dol[j]].numer := 0; |
| 48 | P := P^.nast |
| 49 | end |
| 50 | {ile = liczba różnych wierzchołków warstwy.} |
| 51 | end |
Pełną treść przedstawionego rozwiązania można znaleźć na załączonej dyskietce.
Zanalizujmy koszt działania opisanego algorytmu. Z każdym wierzchołkiem i każdą krawędzią jest związana stała ilość informacji. Liczba krawędzi jest liniowa ze względu na liczbę wierzchołków. Tak więc złożoność pamięciowa opisanego algorytmu wynosi 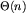 , gdzie n jest liczbą wierzchołków.
, gdzie n jest liczbą wierzchołków.
Podział wierzchołków na warstwy wymaga czasu 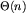 . Posortowanie wierzchołków i-tej warstwy według ich kodów wymaga czasu
. Posortowanie wierzchołków i-tej warstwy według ich kodów wymaga czasu 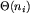 . Sklejenie wierzchołków z i-tej warstwy o tej samej charakterystyce wymaga czasu
. Sklejenie wierzchołków z i-tej warstwy o tej samej charakterystyce wymaga czasu 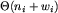 . Tak więc łączny czas działania opisanego algorytmu wynosi
. Tak więc łączny czas działania opisanego algorytmu wynosi
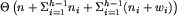 Zauważmy jednak, że
Zauważmy jednak, że 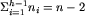 oraz, że
oraz, że 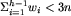 . Stąd czas działania opisanego algorytmu wynosi
. Stąd czas działania opisanego algorytmu wynosi 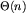 .
.
Binarne diagramy decyzyjne
Opisywane zadanie ma związek z tzw. binarnymi diagramami decyzyjnymi (ang. phbinary decision diagrams, w skrócie BDD) - stosowaną w praktyce strukturą danych. Struktura ta służy do zwięzłego reprezentowania formuł rachunku zdań. Przyjmijmy, że w formułach może się pojawiać k różnych zmiennych zdaniowych: x_1, ..., x_k. Podobnie jak w przypadku labiryntu Bajtosmoka, BDD ma postać multigrafu skierowanego. Wierzchołki tego multigrafu są podzielone na k+1 warstw, o głębokościach 0-k. Warstwę o głębokości 0 tworzą dokładnie dwa wierzchołki, reprezentujące prawdę i fałsz - tak jakby były dwie smocze jamy. Z każdego wierzchołka należącego do pozostałych warstw wychodzą dokładnie po dwie krawędzie, jedna z etykietą "prawda" i jedna z etykietą "fałsz" (zamiast trzech krawędzi ponumerowanych 1, 2 i 3). Krawędzie wychodzące z danego wierzchołka muszą prowadzić do wierzchołków należących do warstwy o głębokości o 1 mniejszej. Warstwę o głębokości k tworzy dokładnie jeden wierzchołek - odpowiednik wejścia do labiryntu. Zauważmy, że wszystkie ścieżki prowadzące z tego wierzchołka do wierzchołków reprezentujących prawdę i fałsz mają długość k+1.
W jaki sposób możemy traktować BDD jak formułę rachunku zdań? Dla zadanego wartościowania zmiennych zdaniowych (tzn. przypisania zmiennym zdaniowym wartości prawda/fałsz) formuła rachunku zdań jest albo prawdziwa, albo fałszywa. Aby odczytać, czy dla zadanego wartościowania zmiennych zdaniowych BDD jest prawdziwe, czy fałszywe musimy przejść przez BDD zgodnie z "planem podróży" wyznaczonym przez wartościowanie zmiennych. Przejście zaczynamy od jedynego wierzchołka należącego do warstwy o głębokości k. Między wierzchołkami przechodzimy wzdłuż krawędzi - będąc w wierzchołku należącym do warstwy o głębokości h wybieramy tę krawędź, która ma etykietę równą wartości zmiennej xh. Wartość BDD dla danego wartościowania jest taka, jak etykieta wierzchołka, do którego docieramy na końcu przejścia.
Poniższy rysunek przedstawia BDD reprezentujące formułę 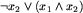 .
.
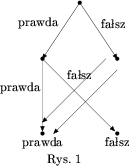
Zauważmy, że dla każdej formuły rachunku zdań istnieje BDD reprezentujące daną formułę. BDD takie możemy łatwo zbudować. Weźmy pełne drzewo binarne wysokości k+1. Krawędzie wychodzące z wierzchołków na lewo etykietujemy prawdą, a wychodzące na prawo fałszem. Zauważmy, że każdemu wartościowaniu zmiennych zdaniowych odpowiada dokładnie jeden liść - ten, do którego prowadzi z korzenia drzewa przejście zgodne z wartościowaniem. Liście drzewa etykietujemy prawdą i fałszem, zgodnie z tym jaka jest wartość formuły dla wartościowania zmiennych odpowiadającego danemu liściowi. Jeżeli skleimy liście mające takie same etykiety (i ew. dodamy jeden wierzchołek, jeżeli wszystkie liście mają takie same etykiety), to uzyskujemy BDD reprezentujące daną formułę.
Zauważmy, że formuła rachunku zdań jest tautologią wtw. gdy w reprezentującym ją BDD żadna krawędź nie prowadzi do wierzchołka reprezentującego fałsz.
Omawiane zadanie odpowiada przekształceniu BDD na równoważne o minimalnej liczbie wierzchołków. Takie BDD stosuje się jako formę zwięzłego reprezentowania formuł rachunku zdań. Warto nadmienić, że dwie formuły rachunku zdań są sobie równoważne wtedy i tylko wtedy, gdy minimalne BDD reprezentujące te formuły są takie same.
Testy
Do sprawdzania rozwiązań zawodników użyto 14-tu testów. Oto ich krótka charakterystyka:
LAB1.IN - prosty test badający poprawność rozwiązań, n=10,
LAB2.IN - test losowy badający poprawność rozwiązań, n=50,
LAB3.IN - test losowy badający poprawność rozwiązań, n=200,
LAB4.IN - w tym teście plan labiryntu składa się z 335 warstw, a każda warstwa z 3 wierzchołków: czerwonego, zielonego i niebieskiego, (z wyjątkiem najpłytszej i najgłębszej warstwy, które mają po jednym wierzchołku); z każdego wierzchołka prowadzą krawędzie łączące go z wszystkimi wierzchołkami o głębokości o 1 mniejszej; żadne wierzchołki nie są sklejane ze sobą,
LAB5.IN - prosty test badający poprawność rozwiązań, n=12,
LAB6.IN - w tym teście plan labiryntu ma kształt pełnego drzewa wysokości 8, plus smocza jama; wszystkie wierzchołki z jednej warstwy są tego samego koloru, a kolejne warstwy mają kolory dobierane na przemian; w każdej warstwie wszystkie wierzchołki są sklejane ze sobą,
LAB7.IN - losowy test badający efektywność rozwiązań, wszystkie wierzchołki są tego samego koloru, n=6 000, 558 sklejeń wierzchołków,
LAB8.IN - losowy test badający efektywność rozwiązań, wszystkie wierzchołki są tego samego koloru, n=6 000, 51 sklejeń wierzchołków,
LAB9.IN - losowy test badający efektywność rozwiązań, wszystkie wierzchołki są tego samego koloru, n=6 000, żadne wierzchołki nie są sklejane ze sobą,
LAB10.IN - prosty test badający poprawność rozwiązań, n=12,
LAB11.IN - test badający efektywność rozwiązań, wszystkie wierzchołki są tego samego koloru, n=6 000, dla każdego 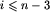 z wierzchołka nr i prowadzą krawędzie do wierzchołków o numerach i+1, i+2 i i+3, z wierzchołka nr n-2 prowadzi jedna krawędź do wierzchołka nr n-1 i dwie krawędzie do wierzchołka nr n, a z wierzchołka nr n-1 wszystkie krawędzie prowadzą do wierzchołka nr n; żadne wierzchołki nie są sklejane ze sobą,
LAB12.IN - prosty test badający poprawność rozwiązań, n=12,
LAB13.IN - test badający efektywność rozwiązań, wszystkie wierzchołki są tego samego koloru, n=6 000, każda warstwa składa się z dokładnie jednego wierzchołka, krawędzie wychodzące z każdego wierzchołka prowadzą do (jedynego) wierzchołka o głębokości o jeden mniejszej; żadne wierzchołki nie są sklejane ze sobą,
LAB14.IN - prosty test badający poprawność rozwiązań, n=12.
z wierzchołka nr i prowadzą krawędzie do wierzchołków o numerach i+1, i+2 i i+3, z wierzchołka nr n-2 prowadzi jedna krawędź do wierzchołka nr n-1 i dwie krawędzie do wierzchołka nr n, a z wierzchołka nr n-1 wszystkie krawędzie prowadzą do wierzchołka nr n; żadne wierzchołki nie są sklejane ze sobą,
LAB12.IN - prosty test badający poprawność rozwiązań, n=12,
LAB13.IN - test badający efektywność rozwiązań, wszystkie wierzchołki są tego samego koloru, n=6 000, każda warstwa składa się z dokładnie jednego wierzchołka, krawędzie wychodzące z każdego wierzchołka prowadzą do (jedynego) wierzchołka o głębokości o jeden mniejszej; żadne wierzchołki nie są sklejane ze sobą,
LAB14.IN - prosty test badający poprawność rozwiązań, n=12.
W testach nr 4, 9, 11 i 13 nie było żadnych sklejeń wierzchołków. Testy te zostały zgrupowane z prostymi testami badającymi poprawność rozwiązań (4 z 5, 9 z 10, 11 z 12 oraz 13 z 14) - oceniane rozwiązanie otrzymywało punkty za testy z danej grupy tylko wtedy, gdy uzyskiwało punkty za obydwa testy tworzące grupę. Takie grupowanie testów pozwalało wychwycić rozwiązania stwierdzające zawsze, że żadne wierzchołki nie ulegają sklejeniu.
Poniższa tabelka przedstawia wielkości poszczególnych testów oraz wyniki.

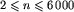 , będąca liczbą komnat (łącznie ze smoczą jamą). Komnaty są ponumerowane od 1 do n tak, że komnaty o większych numerach znajdują się niżej (komnata, w której znajduje się wejście do labiryntu ma numer 1, a smocza jama ma numer n). W kolejnych n-1 wierszach pliku są opisane komnaty (poza smoczą jamą) oraz studnie prowadzące od nich w dół. W każdym z tych wierszy znajduje się litera, po niej jeden znak odstępu, a następnie trzy liczby całkowite oddzielone pojedynczymi odstępami. Litera oznacza kolor komnaty (C - czerwony, Z - zielony, N - niebieski), a i-ta liczba (dla i = 1, 2, 3) jest numerem komnaty, do której prowadzi i-ta studnia.
, będąca liczbą komnat (łącznie ze smoczą jamą). Komnaty są ponumerowane od 1 do n tak, że komnaty o większych numerach znajdują się niżej (komnata, w której znajduje się wejście do labiryntu ma numer 1, a smocza jama ma numer n). W kolejnych n-1 wierszach pliku są opisane komnaty (poza smoczą jamą) oraz studnie prowadzące od nich w dół. W każdym z tych wierszy znajduje się litera, po niej jeden znak odstępu, a następnie trzy liczby całkowite oddzielone pojedynczymi odstępami. Litera oznacza kolor komnaty (C - czerwony, Z - zielony, N - niebieski), a i-ta liczba (dla i = 1, 2, 3) jest numerem komnaty, do której prowadzi i-ta studnia.
 nil do begin
nil do begin  do begin
do begin 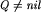 do begin
do begin 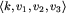 , gdzie k to kolor wierzchołka, a v_1, v_2, v_3, to wierzchołki, do których prowadzą krawędzie wychodzące z danego wierzchołka. Przetwarzając wierzchołki z kolejnej warstwy sklejamy wierzchołki o takich samych kodach. Jak jednak wyznaczyć, które wierzchołki mają takie same kody? Możemy skorzystać ze struktury słownikowej (dowolnego rodzaju, o dostępie w czasie logarytmicznym) - w momencie, gdy wstawiamy do struktury kod, który już w nim jest, to odpowiednie wierzchołki należy skleić. W ten sposób wyznaczenie wierzchołków do sklejenia wymaga czasu
, gdzie k to kolor wierzchołka, a v_1, v_2, v_3, to wierzchołki, do których prowadzą krawędzie wychodzące z danego wierzchołka. Przetwarzając wierzchołki z kolejnej warstwy sklejamy wierzchołki o takich samych kodach. Jak jednak wyznaczyć, które wierzchołki mają takie same kody? Możemy skorzystać ze struktury słownikowej (dowolnego rodzaju, o dostępie w czasie logarytmicznym) - w momencie, gdy wstawiamy do struktury kod, który już w nim jest, to odpowiednie wierzchołki należy skleić. W ten sposób wyznaczenie wierzchołków do sklejenia wymaga czasu 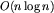 , gdzie n jest liczbą wierzchołków. Jeżeli zamiast słownika o dostępie w czasie logarytmicznym użyjemy tablicy haszującej, to możemy uzyskać oczekiwany czas O(n).
, gdzie n jest liczbą wierzchołków. Jeżeli zamiast słownika o dostępie w czasie logarytmicznym użyjemy tablicy haszującej, to możemy uzyskać oczekiwany czas O(n).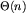 . Oznaczmy przez h głębokość wierzchołka z wejściem do labiryntu, przez ni oznaczmy liczbę wierzchołków w warstwie głębokości i. Zauważmy, że n_0 = n_h = 1 oraz
. Oznaczmy przez h głębokość wierzchołka z wejściem do labiryntu, przez ni oznaczmy liczbę wierzchołków w warstwie głębokości i. Zauważmy, że n_0 = n_h = 1 oraz 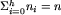 . W i-tym kroku drugiej fazy algorytmu sklejamy w i-tej warstwie wierzchołki o takich samych kodach. Z i-tej warstwy wychodzi 3ni krawędzi prowadzących do co najwyżej 3ni wierzchołków. Wierzchołki te możemy wyznaczyć i ponumerować w czasie rzędu ni. W kodach wierzchołków z i-tej warstwy wierzchołki, do których prowadzą krawędzie możemy reprezentować za pomocą numerów w tej numeracji. Wówczas możemy posortować kody leksykograficznie w czasie rzędu ni.
. W i-tym kroku drugiej fazy algorytmu sklejamy w i-tej warstwie wierzchołki o takich samych kodach. Z i-tej warstwy wychodzi 3ni krawędzi prowadzących do co najwyżej 3ni wierzchołków. Wierzchołki te możemy wyznaczyć i ponumerować w czasie rzędu ni. W kodach wierzchołków z i-tej warstwy wierzchołki, do których prowadzą krawędzie możemy reprezentować za pomocą numerów w tej numeracji. Wówczas możemy posortować kody leksykograficznie w czasie rzędu ni.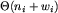 . Poniższy fragment kodu skleja odpowiednie wierzchołki.
. Poniższy fragment kodu skleja odpowiednie wierzchołki.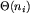 . Sklejenie wierzchołków z i-tej warstwy o tej samej charakterystyce wymaga czasu
. Sklejenie wierzchołków z i-tej warstwy o tej samej charakterystyce wymaga czasu 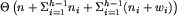
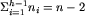 oraz, że
oraz, że 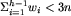 . Stąd czas działania opisanego algorytmu wynosi
. Stąd czas działania opisanego algorytmu wynosi 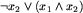 .
.
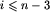 z wierzchołka nr i prowadzą krawędzie do wierzchołków o numerach i+1, i+2 i i+3, z wierzchołka nr n-2 prowadzi jedna krawędź do wierzchołka nr n-1 i dwie krawędzie do wierzchołka nr n, a z wierzchołka nr n-1 wszystkie krawędzie prowadzą do wierzchołka nr n; żadne wierzchołki nie są sklejane ze sobą,
z wierzchołka nr i prowadzą krawędzie do wierzchołków o numerach i+1, i+2 i i+3, z wierzchołka nr n-2 prowadzi jedna krawędź do wierzchołka nr n-1 i dwie krawędzie do wierzchołka nr n, a z wierzchołka nr n-1 wszystkie krawędzie prowadzą do wierzchołka nr n; żadne wierzchołki nie są sklejane ze sobą,
