| Wojciech Rytter | Marcin Stefaniak |
| Treść zadania, Opracowanie | Program wzorcowy |
Liczby antypierwsze
Oznaczmy przez 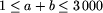 liczbę dzielników liczby i (włącznie z 1 i i). Dodatnią liczbę całkowitą nazywamy antypierwszą, gdy ma ona więcej dzielników niż wszystkie dodatnie liczby całkowite mniejsze od niej. Przykładowymi liczbami antypierwszymi są liczby: 1, 2, 4, 6, 12 i 24.
liczbę dzielników liczby i (włącznie z 1 i i). Dodatnią liczbę całkowitą nazywamy antypierwszą, gdy ma ona więcej dzielników niż wszystkie dodatnie liczby całkowite mniejsze od niej. Przykładowymi liczbami antypierwszymi są liczby: 1, 2, 4, 6, 12 i 24.
Zadanie
Napisz program, który:
- wczyta z pliku tekstowego ant.in dodatnią liczbę całkowitą n,
- wyznaczy największą liczbę antypierwszą nie przekraczającą n,
- zapisze wyznaczoną liczbę w pliku tekstowym ant.out.
Wejście
W jedynym wierszu pliku tekstowego ant.in znajduje się jedna liczba całkowita n, 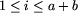 .
.
Wyjście
W jedynym wierszu pliku ant.out Twój program powinien zapisać dokładnie jedną liczbę całkowitą - największą liczbę antypierwszą nie przekraczającą n.
Przykład
Dla pliku wejściowego ant.in
1000
poprawną odpowiedzią jest plik wyjściowy ant.out
840
Rozwiązanie
Efektywne rozwiązanie zadania opiera się na prostych własnościach liczb antypierwszych:
- liczb antypierwszych mniejszych od zadanego n jest bardzo mało;
- liczby antypierwsze mają bardzo proste rozkłady względem liczb pierwszych;
- liczby pierwsze występujące w tych rozkładach są małe.
Aby obliczyć liczbę dzielników liczby n>1, można rozłożyć ją na czynniki pierwsze. Jeśli
to
Widać, że liczba dzielników danej liczby nie zależy od wielkości liczb pierwszych występujących w jej rozkładzie na czynniki pierwsze, a jedynie od krotności, z jaką do tego rozkładu wchodzą.
Przykład
Przykładowymi liczbami antypierwszymi są liczby 1, 2, 4, 6, 12, 24 oraz duże liczby:
27935107200 = 27335271111131171191 2248776129600 = 26335272111131171191231
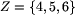

Przyjmijmy, że przez pi rozumiemy i-tą kolejną liczbę pierwszą, a przez ai rozumiemy krotność pi w rozkładzie n na czynniki pierwsze (możliwe, że ai = 0).
Jeżeli ciąg liczb ai nie jest nierosnący, to n nie może być liczbą antypierwszą, gdyż wtedy moglibyśmy tak zamienić miejscami pewne krotności, że otrzymalibyśmy mniejszą liczbę o tej samej liczbie dzielników. Dlatego możemy ograniczyć poszukiwania liczb antypierwszych do liczb o ,,nierosnących'' rozkładach na czynniki pierwsze. Łatwo możemy wygenerować wszystkie takie rozkłady dla liczb nie przekraczających danego ograniczenia górnego (kolejne rozkłady wyznaczamy w porządku leksykograficznym).
Jak się okazuje, liczb antypierwszych 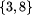 jest niedużo, dokładnie 68. Pierwsze 41 liczb antypierwszych przedstawiono w poniższej tabeli, razem z potęgami w rozkładach na kolejne liczby pierwsze.
jest niedużo, dokładnie 68. Pierwsze 41 liczb antypierwszych przedstawiono w poniższej tabeli, razem z potęgami w rozkładach na kolejne liczby pierwsze. 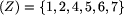
Niech p1, p2, ..., pt będzie najdłuższym ciągiem kolejnych liczb pierwszych takich, że ich iloczyn nie przekracza n. Liczymy najpierw t. Istotnym jest to, że t jest stosunkowo małe, zatem liczba liczb pierwszych i ciągów do rozważenia nie jest bardzo duża. Aby znaleźć największą liczbę antypierwszą mniejszą lub równą n, rozważmy (najlepiej w kolejności leksykograficznej) wszystkie ciągi i1, i2, ... it spełniające dwa poniższe warunki.
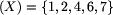
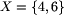 Jak się okazuje, takich ciągów, potencjalnych kandydatów na liczby antypierwsze
Jak się okazuje, takich ciągów, potencjalnych kandydatów na liczby antypierwsze 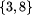 , jest niedużo - około 1500. Bez trudu możemy więc je przesortować i jeden raz przeglądając znaleźć największą liczbę antypierwszą nie przekraczającą danego ograniczenia górnego.
, jest niedużo - około 1500. Bez trudu możemy więc je przesortować i jeden raz przeglądając znaleźć największą liczbę antypierwszą nie przekraczającą danego ograniczenia górnego.
Obserwacja
Przyjrzyjmy się strukturze pierwszych 40 liczb antypierwszych. W tabeli pokazane są wszystkie liczby antypierwsze mniejsze od 3 milionów. Zauważmy, że ostatnie potęgi, poza dwoma przypadkami, są równe 1. Przedostatnie potęgi są też nieduże. Nie jest to przypadek, ponieważ zachodzi poniższy fakt (dosyć trudny do uzasadnienia, ale prawdziwy). Korzystając z tego można ograniczyć przestrzeń rozpatrywanych danych.
Fakt
Dla każdej liczby antypierwszej, oprócz liczb 2 i 36, ostatnia potęga w rozkładzie na liczby pierwsze jest równa 1, natomiast potęgi druga i trzecia od końca nie przekraczają nigdy 4.
Zauważmy olbrzymią różnicę w liczbie liczb antypierwszych mniejszych od zadanej liczby n (dostatecznie dużej) w porównaniu z liczbą liczb pierwszych. Właśnie dzięki temu testowanie liczb antypierwszych jest znacznie łatwiejsze od testowania liczb pierwszych.
Testy
Zadanie testowane było na zestawie 21 danych testowych.
- ant0.in - n = 1000, wynik: 840;
- ant1.in - n = 1, wynik: 1;
- ant2.in - n = 3, wynik: 2;
- ant3.in - n = 5, wynik: 4;
- ant4.in - n = 100000, wynik: 83160;
- ant5.in - n = 8, wynik: 6;
- ant6.in - n = 5041, wynik: 5040;
- ant7.in - n = 20159, wynik: 15120;
- ant8.in - n = 15120, wynik: 15120;
- ant9.in - n = 75000, wynik: 55440;
- ant10.in - n = 150000, wynik: 110880;
- ant11.in - n = 1000000, wynik: 720720;
- ant12.in - n = 3000, wynik: 2520;
- ant13.in - n = 8000000, wynik: 7207200;
- ant14.in - n = 15000000, wynik: 14414400;
- ant15.in - n = 30000, wynik: 27720;
- ant16.in - n = 60000000, wynik: 43243200;
- ant17.in - n = 110000000, wynik: 73513440;
- ant18.in - n = 354218765, wynik: 294053760;
- ant19.in - n = 600000000, wynik: 551350800;
- ant20.in - n = 1000000000, wynik: 735134400;
- ant21.in - n = 2000000000, wynik: 1396755360.
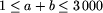 liczbę dzielników liczby i (włącznie z 1 i i). Dodatnią liczbę całkowitą nazywamy antypierwszą, gdy ma ona więcej dzielników niż wszystkie dodatnie liczby całkowite mniejsze od niej. Przykładowymi liczbami antypierwszymi są liczby: 1, 2, 4, 6, 12 i 24.
liczbę dzielników liczby i (włącznie z 1 i i). Dodatnią liczbę całkowitą nazywamy antypierwszą, gdy ma ona więcej dzielników niż wszystkie dodatnie liczby całkowite mniejsze od niej. Przykładowymi liczbami antypierwszymi są liczby: 1, 2, 4, 6, 12 i 24.
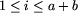 .
.
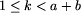
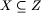
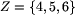

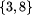 jest niedużo, dokładnie 68. Pierwsze 41 liczb antypierwszych przedstawiono w poniższej tabeli, razem z potęgami w rozkładach na kolejne liczby pierwsze.
jest niedużo, dokładnie 68. Pierwsze 41 liczb antypierwszych przedstawiono w poniższej tabeli, razem z potęgami w rozkładach na kolejne liczby pierwsze.