| Marcin Kubica | Marcin Sawicki |
| Treść zadania, Opracowanie | Program wzorcowy |
Bank
W Bajtocji funkcjonują cztery rodzaje waluty:
denary, franki, grosze i talary, nie wymienialne między sobą.
Przysparza to wiele kłopotów mieszkańcom Bajtocji.
Bajtocki Bank Biznesu (w skrócie BBB) na skutek pomyłki w rodzaju
waluty stanął w obliczu utraty płynności gotówkowej.
Zawarł on z klientami szereg umów na kredytowanie różnych
przedsięwzięć.
Wszystkie te umowy są zawarte według takiego samego wzoru:
- umowa określa maksymalną wysokość kredytu w każdym rodzaju waluty,
- w ramach tak określonego limitu, gdy klient potrzebuje
gotówki, to zgłasza się do BBB prosząc o określoną sumę w
każdym rodzaju waluty;
BBB może dowolnie długo zwlekać z wypłaceniem pieniędzy, ale
dopóki klient nie przekracza maksymalnej wysokości kredytu, to
prędzej czy później musi je klientowi wypłacić,
- po otrzymaniu pieniędzy klient może zgłaszać się po kolejne
transze, aż do wyczerpania limitu,
- na koniec klient spłaca całość zaciągniętego kredytu,
może z tym zwlekać dowolnie długo, ale prędzej czy później
musi spłacić kredyt,
- klient nie ma obowiązku wykorzystania kredytu w maksymalnej
wysokości,
- dla uproszczenia zakładamy, że klienci nie płacą żadnych
odsetek ani prowizji.
BBB nie dysponuje wystarczającą ilością gotówki, aby zaspokoić
potrzeby swoich klientów, a bez ich wcześniejszego zaspokojenia
kredyty nie będą spłacane.
BBB poprosił Bajtocki Fundusz Walutowy (w skrócie BFW) o pomoc.
BFW zgodził się pomóc BBB, ale zażądał, żeby BBB określił
minimalne kwoty każdego rodzaju waluty, jakie BBB musi posiadać, aby
móc doprowadzić do spłacenia przez klientów wszystkich kredytów
(nawet jeżeli klienci będą chcieli wykorzystać swoje kredyty do
maksymalnej ich wysokości).
Specjaliści BBB odkryli, że możliwych jest wiele odpowiedzi na
tak postawione pytanie (por. przykład).
BFW odpowiedziało, że interesują ich dowolne takie kwoty poszczególnych
rodzajów walut, że gdyby zmniejszyć którąkolwiek z nich choćby o 1, to
mogłyby nie wystarczyć do zakończenia realizacji wszystkich kredytów.
Zadanie
Napisz program, który:
- wczyta z pliku ban.in maksymalne i aktualne wysokości
kredytów klientów,
- wyznaczy minimalne kwoty poszczególnych rodzajów walut gwarantujące
możliwość realizacji wszystkich kredytów,
- zapisze wynik w pliku ban.out.
Jeśli jest możliwych wiele wyników, to Twój program powinien
zapisać dowolny z nich.
Wejście
W pierwszym wierszu pliku tekstowego ban.in jest zapisana
jedna dodatnia liczba całkowita n równa liczbie klientów,
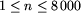 .
Klienci są ponumerowani od 1 do n.
W kolejnych n wierszach jest zapisanych po osiem
nieujemnych liczb całkowitych.
W i+1-szym wierszu (dla i=1,...,n) zapisane są liczby
.
Klienci są ponumerowani od 1 do n.
W kolejnych n wierszach jest zapisanych po osiem
nieujemnych liczb całkowitych.
W i+1-szym wierszu (dla i=1,...,n) zapisane są liczby
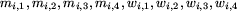 ,
(
,
(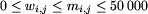 , dla j=1,...,4).
Liczby
, dla j=1,...,4).
Liczby 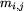 i
i 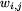 określają odpowiednio maksymalną i
aktualną wysokość kredytu klienta nr i w:
denarach (j=1), frankach (j=2), groszach (j=3) i
talarach (j=4).
określają odpowiednio maksymalną i
aktualną wysokość kredytu klienta nr i w:
denarach (j=1), frankach (j=2), groszach (j=3) i
talarach (j=4).
Wyjście
Twój program powinien zapisać w pierwszym (i jedynym) wierszu
pliku tekstowego ban.out cztery nieujemne liczby całkowite,
pooddzielane pojedynczymi odstępami, określające minimalne kwoty
gotówki, jakie musi posiadać BBB, odpowiednio w
denarach, frankach, groszach i talarach.
Przykład
Dla pliku wejściowego ban.in:
4
3 2 1 2 0 2 0 1
2 4 1 8 1 2 1 1
3 2 0 3 1 0 0 1
3 0 1 2 1 0 0 1
poprawną odpowiedzią może być plik tekstowy ban.out:
1 2 0 7
lub:
2 0 1 4
Zakleszczenie i algorytm bankiera
Zadanie to jest związane ze zjawiskiem zakleszczenia oraz algorytmem
bankiera używanym do unikania zakleszczenia
(zobacz [28], p. 7.5.3).
Zjawisko zakleszczenia występuje w systemach operacyjnych, w których
współbieżnie (tzn. równocześnie) może być wykonywanych wiele
procesów (działających programów).
Procesy te mogą używać rozmaitych zasobów systemowych, takich jak
pamięć, czy urządzenia wejścia/wyjścia.
Zasoby te są przydzielane procesom przez system operacyjny.
Zakleszczenie występuje wówczas, gdy kilka procesów czeka nawzajem na
siebie, prosząc system o przydzielenie zasobów, które są zajęte przez
pozostałe procesy.
Wyobraźmy sobie na przykład, że w systemie jest jeden napęd CD-ROM
i jedna karta dźwiękowa, oraz że dwa procesy (P1 i P2)
chcą uzyskać wyłączny dostęp do tych urządzeń.
Załóżmy przy tym, że P1 uzyskał już dostęp do CD-ROM'u
i czeka na zwolnienie karty dźwiękowej, a P2 ma już dostęp
do karty dźwiękowej i czeka na zwolnienie CD-ROM'u.
Jak łatwo zauważyć, te dwa procesy będą na siebie czekać w
nieskończoność.
Takie zjawisko nazywamy zakleszczeniem.
Oczywiście zakleszczenie jest zjawiskiem niepożądanym.
Jeden ze sposobów radzenia sobie z zakleszczeniem polega na
takim przydzielaniu przez system operacyjny zasobów procesom, aby
unikać zakleszczenia.
Pomysł polega na tym, aby utrzymywać system w bezpiecznym
stanie, tzn. takim stanie, w którym mamy gwarancje, że wszystkie
działające procesy mogą zostać wykonane aż do końca, bez
zakleszczenia.
System operacyjny przydziela zasoby procesom tylko wtedy, gdy
prowadzi to do bezpiecznego stanu.
W rezultacie, może się zdarzyć, że ze względów bezpieczeństwa
proces musi czekać, mimo że potrzebne mu zasoby są dostępne.
W celu stwierdzenia czy stan systemu jest bezpieczny używany jest
algorytm bankiera.
Algorytm ten potrzebuje dodatkowej informacji:
maksymalnych ilości zasobów jakie mogą być potrzebne poszczególnym
procesom.
Procesy deklarują maksymalne ilości potrzebnych zasobów w
momencie uruchomienia.
Algorytm bankiera opiera się na analogii między systemem
operacyjnym, a opisanym w treści zadania systemem bankowym.
Różne rodzaje zasobów to różne, wzajemnie nie
wymienialne między sobą waluty.
Klienci to procesy działające w systemie, a BBB to system
operacyjny.
Środki pieniężne jakimi dysponuje BBB to wolne zasoby, a pieniądze
pożyczone klientom to zasoby przydzielone procesom.
Natomiast maksymalne ilości potrzebnych zasobów deklarowane
przez procesy, to
wysokości limitów określone w umowach kredytowych.
Algorytm bankiera opiera się na następujących obserwacjach.
Jeżeli w danym stanie system może doprowadzić do zakończenia
wszystkich procesów, to może to również zrobić wykonując i kończąc
te procesy w pewnej kolejności, po jednym na raz.
Aby móc zakończyć jakiś proces, musimy mieć w systemie
tyle wolnych zasobów, żeby zaspokoić jego potrzeby.
W najgorszym przypadku ilość potrzebnych zasobów jest równa
różnicy między maksymalną zadeklarowaną liczbą potrzebnych
zasobów, a ilością aktualnie przydzielonych zasobów.
Jednak po zakończeniu procesu w systemie może tylko przybyć wolnych
zasobów, gdyż wszystkie zasoby przydzielone procesowi są
zwalniane.
Tak więc, aby odpowiedzieć na pytanie czy sytuacja jest
bezpieczna, musimy stwierdzić, czy istnieje taka kolejność
P1, P2, ..., Pn, w której możemy wykonywać i
kończyć procesy.
Ponadto, taką kolejność możemy konstruować w sposób zachłanny -
jeżeli istnieje taka kolejność i wolne w danej chwili zasoby
wystarczają do zakończenia procesu P, to istnieje również taka
kolejność zaczynająca się od P.
Niech n będzie liczbą procesów, a m liczbą rodzajów zasobów (w
naszym przypadku m=4).
Zakładamy, że są określone następujące cztery tablice:
- wolne - wektor długości m określający ilości
wolnych zasobów poszczególnych rodzajów,
- maks - macierz
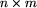 określająca
zadeklarowane przez poszczególne procesy maksymalne ilości
potrzebnych im zasobów,
określająca
zadeklarowane przez poszczególne procesy maksymalne ilości
potrzebnych im zasobów,
- przydzielone - macierz
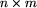 określająca ilości
zasobów przydzielonych poszczególnym procesom,
określająca ilości
zasobów przydzielonych poszczególnym procesom,
- potrzebne - macierz
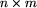 określająca maksymalne
ilości zasobów potrzebnych do zakończenia poszczególnych
procesów; tę macierz możemy zawsze wyznaczyć na podstawie wzoru
określająca maksymalne
ilości zasobów potrzebnych do zakończenia poszczególnych
procesów; tę macierz możemy zawsze wyznaczyć na podstawie wzoru
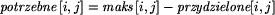 .
.
Dodatkowo zakładamy, że mamy do dyspozycji dwa pomocnicze wektory:
pom i zakończone długości odpowiednio m i n.
Wektor pom reprezentuje symulowaną ilość wolnych zasobów, a
zakończone reprezentuje zbiór procesów, które udało się
zakończyć.
Algorytm bankiera ma następującą postać:
| 1 | pom := wolne; |
| 2 | zakończone := (false, false, ..., false); |
| 3 | while istnieje takie i, że: |
| 4 | not zakończone[i] and 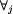 potrzebne[i, j] potrzebne[i, j]  pom[j] pom[j] |
| 5 | do begin |
| 6 | for j := 1 to m do |
| 7 | pom[j] := pom[j] + przydzielone[i, j]; |
| 8 | zakończone[i] := true |
| 9 | end; |
| 10 | if zakończone = (true, true, ..., true) then |
| 11 | system jest w stanie bezpiecznym |
| 12 | end |
| 13 | system nie jest w stanie bezpiecznym. |
Algorytm ten ma złożoność O(n2m).
Algorytm bankiera jest zwykle używany do określenia, czy stan
systemu po przydzieleniu zasobów jest bezpieczny.
W niniejszym zadaniu problem jest postawiony trochę inaczej.
System znalazł się w stanie niebezpiecznym i pytanie dotyczy
minimalnej liczby wolnych zasobów potrzebnych do tego, aby stan
był bezpieczny.
Rozwiązanie
Możemy zastosować do rozwiązania tego zadania algorytm bankiera.
Dla określonych danych wejściowych może istnieć wiele poprawnych
wyników.
Nasze rozwiązanie wyznacza wynik, który jest najmniejszy
w porządku leksykograficznym.
Inaczej mówiąc, wyznaczamy najpierw najmniejszą liczbę potrzebnych
denarów, następnie dla tak określonej liczby denarów
najmniejszą liczbę potrzebnych franków, itd.
Liczba potrzebnych denarów jest z jednej strony nieujemna, a z
drugiej nie przekracza sumy limitów na denary we
wszystkich umowach kredytowych.
Konkretną wartość znajdujemy w tym przedziale za pomocą metody
bisekcji, stosując za każdym razem algorytm bankiera i
sprawdzając czy przy danej liczbie denarów i nieograniczonych
zasobach pozostałych walut stan jest bezpieczny - jeżeli
nie, to liczba denarów jest zbyt mała.
Jak wspomnieliśmy powyżej, koszt algorytmu bankiera wynosi
O(n2m).
Jeżeli oznaczymy przez s maksymalną wysokość limitu jednej
waluty w umowie kredytowej, to koszt wyznaczenia minimalnej
liczby potrzebnych denarów wynosi 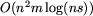 .
Po ustaleniu liczy denarów możemy w podobny sposób wyznaczyć
minimalną liczbę potrzebnych franków, zakładając, że mamy
nieograniczone zasoby groszy i talarów.
Podobnie wyznaczamy minimalną liczbę potrzebnych groszy oraz
talarów.
W ten sposób otrzymujemy rozwiązanie o złożoności rzędu
.
Po ustaleniu liczy denarów możemy w podobny sposób wyznaczyć
minimalną liczbę potrzebnych franków, zakładając, że mamy
nieograniczone zasoby groszy i talarów.
Podobnie wyznaczamy minimalną liczbę potrzebnych groszy oraz
talarów.
W ten sposób otrzymujemy rozwiązanie o złożoności rzędu
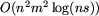 .
.
Okazuje się, że możemy to zadanie rozwiązać bardziej efektywnie.
Tak jak w powyższym algorytmie ustalamy minimalne potrzebne ilości
kolejnych walut.
Powiedzmy, że w kolejnym kroku wyznaczamy minimalną ilość k-tej
waluty.
Wykonujemy wówczas zmodyfikowany algorytm bankiera, który na
podstawie ustalonych ilości walut 1, ..., k-1 i przy
założeniu, że mamy nieograniczone zasoby walut k+1, ..., m, wyznacza
minimalną potrzebną kwotę k-tej waluty.
Symulujemy zakończenie kredytów w pewnej kolejności.
W tym celu symulujemy pulę dostępnych środków pieniężnych oraz
utrzymujemy zbiór kredytów, do zakończenia których mamy
wystarczającą ilość walut 1, ..., k-1.
Symulując kończenie kredytów wybieramy za każdym razem taki
kredyt, do zakończenia którego mamy wystarczająca ilość walut
1, ..., k-1 i który wymaga najmniej środków k-tej waluty.
Jeśli mamy wystarczającą ilość środków, to po prostu
symulujemy zakończenie i spłatę tego kredytu.
Jeśli natomiast brakuje środków k-tej waluty, to odpowiednio
zwiększamy ich ilość.
W ten sposób, po zakończeniu symulacji znamy minimalną wymaganą
ilość środków waluty k.
Aby uzyskać dobrą złożoność takiego algorytmu, musimy zastosować
odpowiednią strukturę danych do przechowywania puli kredytów, do
zakończenia których mamy
wystarczającą ilość walut 1, ..., k-1.
Używamy do tego celu stogów, uporządkowanych według kwoty
określonej waluty potrzebnej do zakończenia kredytu.
Zakładamy, że są zaimplementowane następujące operacje na stogach:
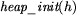 - inicjuje pusty stóg h,
- inicjuje pusty stóg h,
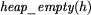 - określa czy stóg h jest pusty,
- określa czy stóg h jest pusty,
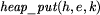 - wkłada na stóg h element e
skojarzony z kluczem k,
- wkłada na stóg h element e
skojarzony z kluczem k,
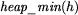 - określa element o najmniejszym
kluczu znajdujący się na stogu h,
- określa element o najmniejszym
kluczu znajdujący się na stogu h,
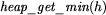 - zdejmuje ze stogu
element o najmniejszym kluczu i przekazuje go jako wynik.
- zdejmuje ze stogu
element o najmniejszym kluczu i przekazuje go jako wynik.
| 1 | const |
| 2 | N_MAX = 8000; |
| 3 | K_MAX = 4; |
| 4 | var |
| 5 | wys_max, wys: array[1..N_MAX, 1..K_MAX] of word; |
| 6 | n: word; |
| 7 | akt: array [1..K_MAX] of longint; |
| 1 | procedure oblicz; |
| 2 | var |
| 3 | heaps: array[1..K_MAX] of heap; |
| 4 | rez: array[1..K_MAX] of longint; |
| 5 | i, j, k, e: word; |
| 6 | zmiana: word; |
| 7 | begin |
| 8 | for i := 1 to K_MAX do akt[i] := 0; |
| 9 | for k := 1 to K_MAX do { Ustalanie limitu na k-tą walutę. } |
| 10 | begin |
| 11 | for i := 1 to k do rez[i] := akt[i]; |
| 12 | for i := 1 to k do heap_init(heaps[i]); |
| 13 | for i := 1 to n do |
| 14 | heap_put(heaps[1], i, wys_max[i,1]-wys[i,1]); |
| 15 | for i := 1 to n do |
| 16 | begin |
| 17 | { Wybieramy kredyty mieszczące się w limitach na waluty 1..k-1. } |
| 18 | for j := 1 to k-1 do |
| 19 | while |
| 20 | (not heap_empty(heaps[j])) and |
| 21 | (heap_min(heaps[j])  rez[j]) rez[j]) |
| 22 | do begin |
| 23 | e := heap_get_min(heaps[j]); |
| 24 | heap_put(heaps[j+1],e,wys_max[e,j+1]-wys[e,j+1]) |
| 25 | end; |
| 26 | { Element wymagający najmniej środków waluty k. } |
| 27 | e := heap_get_min(heaps[k]); |
| 28 | { Czy trzeba zwiększyć akt[k]? } |
| 29 | if rez[k] < wys_max[e,k]-wys[e,k] then |
| 30 | begin |
| 31 | zmiana := wys_max[e,k]-wys[e,k]-rez[k]; |
| 32 | inc(rez[k], zmiana); |
| 33 | inc(akt[k], zmiana) |
| 34 | end; |
| 35 | { Realizujemy kredyt. } |
| 36 | for j := 1 to k do |
| 37 | inc(rez[j], wys[e,j]); |
| 38 | end; |
| 39 | end; |
| 40 | end; |
Algorytm ten jest zaimplementowany przez poniższą procedurę.
Zakładamy przy tym, że zadeklarowane są następujące zmienne:
Zmienna n to liczba kredytów, a tablice wys_max i
wys zawierają odpowiednio limity kredytów i aktualne zadłużenie
klientów.
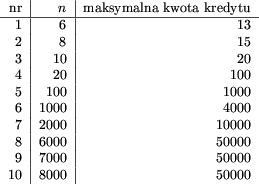
Testy
Testy zostały wygenerowane losowo, przy czym wysokość aktualnie
wykorzystanego kredytu dla żadnej waluty nie przekracza 9.
Poniższa tabelka ilustruje wielkości testów.
Wszystkie testy można znaleźć na załączonej dyskietce.
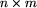 określająca
zadeklarowane przez poszczególne procesy maksymalne ilości
potrzebnych im zasobów,
określająca
zadeklarowane przez poszczególne procesy maksymalne ilości
potrzebnych im zasobów,
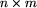 określająca ilości
zasobów przydzielonych poszczególnym procesom,
określająca ilości
zasobów przydzielonych poszczególnym procesom,
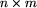 określająca maksymalne
ilości zasobów potrzebnych do zakończenia poszczególnych
procesów; tę macierz możemy zawsze wyznaczyć na podstawie wzoru
określająca maksymalne
ilości zasobów potrzebnych do zakończenia poszczególnych
procesów; tę macierz możemy zawsze wyznaczyć na podstawie wzoru
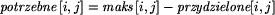 .
.
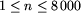 .
Klienci są ponumerowani od 1 do n.
W kolejnych n wierszach jest zapisanych po osiem
nieujemnych liczb całkowitych.
W i+1-szym wierszu (dla i=1,...,n) zapisane są liczby
.
Klienci są ponumerowani od 1 do n.
W kolejnych n wierszach jest zapisanych po osiem
nieujemnych liczb całkowitych.
W i+1-szym wierszu (dla i=1,...,n) zapisane są liczby
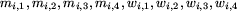 ,
(
,
(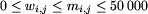 , dla j=1,...,4).
Liczby
, dla j=1,...,4).
Liczby 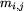 i
i 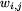 określają odpowiednio maksymalną i
aktualną wysokość kredytu klienta nr i w:
denarach (j=1), frankach (j=2), groszach (j=3) i
talarach (j=4).
określają odpowiednio maksymalną i
aktualną wysokość kredytu klienta nr i w:
denarach (j=1), frankach (j=2), groszach (j=3) i
talarach (j=4).
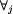 potrzebne[i, j]
potrzebne[i, j]  pom[j]
pom[j]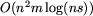 .
Po ustaleniu liczy denarów możemy w podobny sposób wyznaczyć
minimalną liczbę potrzebnych franków, zakładając, że mamy
nieograniczone zasoby groszy i talarów.
Podobnie wyznaczamy minimalną liczbę potrzebnych groszy oraz
talarów.
W ten sposób otrzymujemy rozwiązanie o złożoności rzędu
.
Po ustaleniu liczy denarów możemy w podobny sposób wyznaczyć
minimalną liczbę potrzebnych franków, zakładając, że mamy
nieograniczone zasoby groszy i talarów.
Podobnie wyznaczamy minimalną liczbę potrzebnych groszy oraz
talarów.
W ten sposób otrzymujemy rozwiązanie o złożoności rzędu
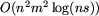 .
.
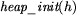 - inicjuje pusty stóg h,
- inicjuje pusty stóg h,
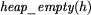 - określa czy stóg h jest pusty,
- określa czy stóg h jest pusty,
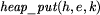 - wkłada na stóg h element e
skojarzony z kluczem k,
- wkłada na stóg h element e
skojarzony z kluczem k,
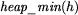 - określa element o najmniejszym
kluczu znajdujący się na stogu h,
- określa element o najmniejszym
kluczu znajdujący się na stogu h,
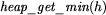 - zdejmuje ze stogu
element o najmniejszym kluczu i przekazuje go jako wynik.
- zdejmuje ze stogu
element o najmniejszym kluczu i przekazuje go jako wynik.
 rez[j])
rez[j]) 