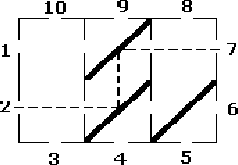Box of Mirrors
Profesor Andrus uwielbia rozwiązywać przeróżne łamigłówki.
Jedną z jego ulubionych jest ``Lustrzana Skrzynka''.
Konstrukcję skrzynki najłatwiej opisać patrząc na nią z góry.
Załóżmy więc, że widzimy poziomy przekrój skrzynki narysowany w prostokątnym
układzie współrzędnych. Jest to prostokąt o bokach równoległych do osi układu
podzielony na 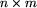 kwadratowych pól
(ułożonych w n wierszy i m kolumn).
W każdym polu może być umieszczone lustro.
Lustro jest ustawione pionowo po przekątnej pola biegnącej od
lewego-dolnego do prawego-górnego narożnika (przekroju) pola.
Obie strony lustra odbijają światło.
kwadratowych pól
(ułożonych w n wierszy i m kolumn).
W każdym polu może być umieszczone lustro.
Lustro jest ustawione pionowo po przekątnej pola biegnącej od
lewego-dolnego do prawego-górnego narożnika (przekroju) pola.
Obie strony lustra odbijają światło.
W zewnętrznych ścianach skrzynki, pośrodku każdego wiersza i
każdej kolumny, znajdują się otwory, przez które może wpadać do
wnętrza lub wychodzić na zewnątrz skrzynki wiązka światła.
Przez każdy otwór można wpuścić do wnętrza skrzynki wiązkę światła
jedynie w kierunku prostopadłym do ściany, w której znajduje się otwór.
Taka wiązka odbijając się od lustra zmienia kierunek o 90 stopni.
Gdy wiązka przechodzi przez puste pole (takie, na którym nie ma lustra),
wówczas jej kierunek nie ulega zmianie.
Otwory w ścianach skrzynki są ponumerowane od 1 do
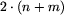 .
Numery są nadawane otworom zgodnie z kolejnością ich występowania
na obwodzie
skrzynki, począwszy od otworu w lewej ścianie górnego-lewego pola
(na przekroju) i następnie w kierunku przeciwnym do ruchu wskazówek
zegara (czyli idąc najpierw w dół lewej ściany).
Ponieważ z zewnątrz nie widać układu luster, więc jedynym sposobem,
by wywnioskować, jaki jest ten układ, jest wpuszczanie wiązek światła
przez wybrane otwory i obserwowanie, przez które otwory
takie wiązki wychodzą.
.
Numery są nadawane otworom zgodnie z kolejnością ich występowania
na obwodzie
skrzynki, począwszy od otworu w lewej ścianie górnego-lewego pola
(na przekroju) i następnie w kierunku przeciwnym do ruchu wskazówek
zegara (czyli idąc najpierw w dół lewej ściany).
Ponieważ z zewnątrz nie widać układu luster, więc jedynym sposobem,
by wywnioskować, jaki jest ten układ, jest wpuszczanie wiązek światła
przez wybrane otwory i obserwowanie, przez które otwory
takie wiązki wychodzą.
Zadanie
Napisz program, który:
- wczyta z pliku tekstowego box.in rozmiar skrzynki i
numery otworów, przez które wpadają i
wychodzą wiązki światła,
- obliczy, na których polach znajdują się lustra, a które pola
są puste,
- zapisze wynik w pliku tekstowym box.out.
Jeżeli istnieje więcej niż jedno rozwiązanie, to program powinien
podać dowolne z nich.
Wejście
W pierwszym wierszu pliku box.in znajdują się dwie liczby
naturalne: n (liczba wierszy pól, 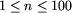 ) oraz
m (liczba kolumn pól,
) oraz
m (liczba kolumn pól, 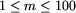 )
oddzielone pojedynczym odstępem.
Każdy z kolejnych
)
oddzielone pojedynczym odstępem.
Każdy z kolejnych 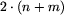 wierszy zawiera po jednej liczbie
naturalnej.
Liczba w (i+1)-szym wierszu oznacza numer otworu, przez który
wyjdzie wiązka światła, która wpada do skrzynki przez otwór o
numerze i.
wierszy zawiera po jednej liczbie
naturalnej.
Liczba w (i+1)-szym wierszu oznacza numer otworu, przez który
wyjdzie wiązka światła, która wpada do skrzynki przez otwór o
numerze i.
Wyjście
Twój program powinien zapisać w pliku wynikowym box.out
n wierszy, z których każdy powinien zawierać m liczb oddzielonych
pojedynczymi odstępami.
Liczba j-ta w i-ym wierszu powinna być równa 1,
jeżeli na polu w i-tym wierszu i j-tej kolumnie
znajduje się lustro; w przeciwnym razie (gdy pole to jest puste)
liczba ta powinna być równa 0.
Przykład
Dla pliku wejściowego box.in
2 3
9
7
10
8
6
5
2
4
1
3
poprawną odpowiedzią jest plik wyjściowy box.out
0 1 0
0 1 1
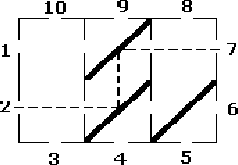
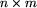 kwadratowych pól
(ułożonych w n wierszy i m kolumn).
W każdym polu może być umieszczone lustro.
Lustro jest ustawione pionowo po przekątnej pola biegnącej od
lewego-dolnego do prawego-górnego narożnika (przekroju) pola.
Obie strony lustra odbijają światło.
kwadratowych pól
(ułożonych w n wierszy i m kolumn).
W każdym polu może być umieszczone lustro.
Lustro jest ustawione pionowo po przekątnej pola biegnącej od
lewego-dolnego do prawego-górnego narożnika (przekroju) pola.
Obie strony lustra odbijają światło.

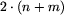 .
Numery są nadawane otworom zgodnie z kolejnością ich występowania
na obwodzie
skrzynki, począwszy od otworu w lewej ścianie górnego-lewego pola
(na przekroju) i następnie w kierunku przeciwnym do ruchu wskazówek
zegara (czyli idąc najpierw w dół lewej ściany).
Ponieważ z zewnątrz nie widać układu luster, więc jedynym sposobem,
by wywnioskować, jaki jest ten układ, jest wpuszczanie wiązek światła
przez wybrane otwory i obserwowanie, przez które otwory
takie wiązki wychodzą.
.
Numery są nadawane otworom zgodnie z kolejnością ich występowania
na obwodzie
skrzynki, począwszy od otworu w lewej ścianie górnego-lewego pola
(na przekroju) i następnie w kierunku przeciwnym do ruchu wskazówek
zegara (czyli idąc najpierw w dół lewej ściany).
Ponieważ z zewnątrz nie widać układu luster, więc jedynym sposobem,
by wywnioskować, jaki jest ten układ, jest wpuszczanie wiązek światła
przez wybrane otwory i obserwowanie, przez które otwory
takie wiązki wychodzą.
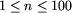 ) oraz
m (liczba kolumn pól,
) oraz
m (liczba kolumn pól, 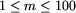 )
oddzielone pojedynczym odstępem.
Każdy z kolejnych
)
oddzielone pojedynczym odstępem.
Każdy z kolejnych