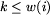Marcin Kubica
Tłumaczenie

Postman

Wiejski listonosz musi dostarczać pocztę wszystkim mieszkańcom okolicy, którzy zamieszkują w wioskach i przy drogach łączących wioski.

Musisz pomóc listonoszowi wytyczyć trasę, która pozwoli mu przejechać wzdłuż każdej drogi i odwiedzić każdą wioskę w okolicy przynajmniej raz. Tak się szczęśliwie składa, że w rozważanych przykładach taka trasa zawsze istnieje. Jednak wytyczone trasy mogą się różnić jakością, tzn. listonosz może otrzymywać różną zapłatę za swą pracę w zależności od wybranej trasy (jak się za chwilę przekonamy, to nie zysk listonosza jest najważniejszy, a zysk jego firmy, czyli poczty). Mieszkańcy każdej wioski chcieliby, by listonosz docierał do nich jak najwcześniej. Każda wioska zawarła więc z pocztą następującą umowę: jeżeli i-ta wioska jest odwiedzana przez listonosza jako k-ta w kolejności (tzn. listonosz odwiedził k-1 różnych wiosek, zanim po raz pierwszy dotarł do wioski i) oraz 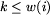kleq w(i), to wioska płaci poczcie w(i)-k euro. Jeśli jednak k>w(i), to wówczas poczta płaci wiosce k-w(i) euro. Ponadto poczta płaci listonoszowi jedno euro za każdy przejazd między dwiema kolejnymi wioskami na jego trasie.

W rozważanej okolicy jest n wiosek, które oznaczamy liczbami naturalnymi od 1 do n. Poczta znajduje się w wiosce oznaczonej numerem 1, a więc trasa listonosza musi rozpoczynać się w tej wiosce. W każdej wiosce zbiega się 2, 4 lub 8 dróg. Pomiędzy dwiema wioskami może istnieć kilka różnych dróg; droga może także powracać do tej samej wioski, z której wyszła.

Zadanie

Twoim zadaniem jest napisanie programu, który: Jeżeli istnieje więcej niż jedno rozwiązanie, to Twój program powinien obliczyć jedno z nich.

Wejście

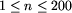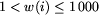W pierwszym wierszu pliku tekstowego pos.in zapisane są dwie liczby naturalne n i m oddzielone pojedynczym odstępem; liczba n (1 le n le 200) oznacza liczbę wiosek, a m jest liczbą dróg. W każdym z kolejnych n wierszy znajduje się jedna liczba naturalna (dodatnia). Liczba w (i+1)-szym wierszu oznacza w(i) (1 < w(i) le 1,000), czyli wstępną kwotę płaconą poczcie przez wioskę numer i (kwota ta jest oczywiście modyfikowana w opisany na początku zadania sposób). W każdym z kolejnych m wierszy znajdują się po dwie liczby naturalne oddzielone pojedynczym odstępem - oznaczają one numery wiosek, które łączy kolejna droga.

Wyjście

Twój program powinien zapisać jedną dodatnią liczbę naturalną k w pierwszym wierszu pliku tekstowego pos.out. W kolejnym wierszu powinno znaleźć się k+1 liczb oznaczających numery wiosek odwiedzanych kolejno przez listonosza w ramach optymalnej trasy. 

6 7
1
7
4
10
20
5
2 4
1 5
2 1
4 5
3 6
1 6
1 3
imgpos1.eps

Przykład

Dla pliku wejściowego pos.in 
6 7
1
7
4
10
20
5
2 4
1 5
2 1
4 5
3 6
1 6
1 3
poprawną odpowiedzią jest plik wyjściowy pos.out 
7
1 5 4 2 1 6 3 1