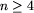 jest sumą dwóch liczb pierwszych.
To jednak nie przybliżyło ich do rozwiązania podstawowego problemu:
czy tak jest naprawdę.
jest sumą dwóch liczb pierwszych.
To jednak nie przybliżyło ich do rozwiązania podstawowego problemu:
czy tak jest naprawdę.
| Wojciech Guzicki, Jarosław Wróblewski | Wojciech Guzicki | Marcin Mucha |
| Treść zadania | Opracowanie | Program wzorcowy |
W roku 1742 C. Goldbach w liście do L. Eulera napisał, że jego zdaniem każda liczba całkowita n>5 jest sumą trzech liczb pierwszych (Liczba pierwsza to liczba naturalna n>1, która ma tylko dwa dzielniki naturalne: 1 oraz n.).
Euler odpisał, że jest to równoważne temu, że każda
liczba parzysta 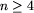 jest sumą dwóch liczb pierwszych.
To jednak nie przybliżyło ich do rozwiązania podstawowego problemu:
czy tak jest naprawdę.
jest sumą dwóch liczb pierwszych.
To jednak nie przybliżyło ich do rozwiązania podstawowego problemu:
czy tak jest naprawdę.
Dziś wiemy, że jest tak dla liczb
aż do 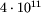 (wiemy też dużo więcej, ale
cała hipoteza jest nadal problemem otwartym).
Nie będziemy tego sprawdzać, postawimy sobie mniej ambitne zadanie.
Okazuje się, że każda liczba naturalna
(wiemy też dużo więcej, ale
cała hipoteza jest nadal problemem otwartym).
Nie będziemy tego sprawdzać, postawimy sobie mniej ambitne zadanie.
Okazuje się, że każda liczba naturalna  jest sumą różnych
nieparzystych liczb pierwszych.
jest sumą różnych
nieparzystych liczb pierwszych.
Twoje zadanie polega na napisaniu programu, który:
Takich rozkładów może być wiele. Twój program może znaleźć jakikolwiek z nich.
W pierwszym wierszu pliku tekstowego gol.in zapisano jedną dodatnią liczbę całkowitą n,
 |
Rozkład liczby k musi być zapisany w dwóch wierszach.
W pierwszym wierszu należy zapisać jedną liczbę całkowitą 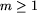 ,
będącą liczbą składników rozkładu.
,
będącą liczbą składników rozkładu.
W drugim wierszu należy zapisać, w rosnącej kolejności, m różnych nieparzystych liczb pierwszych, których suma jest równa k, pooddzielanych pojedynczymi odstępami. Rozkłady powinny występować w kolejności zgodnej z kolejnością liczb w pliku wejściowym.
2 59 15poprawną odpowiedzią jest plik wyjściowy gol.out
5 5 7 11 17 19 3 3 5 7
Istnieje bardzo szybki algorytm pozwalający rozwiązać to
zadanie. Wskażemy mianowicie 32 nieparzyste liczby
pierwsze o tej własności, że każda
dopuszczalna liczba n (tzn. z przedziału
[10;2 000 000 000]) będzie sumą niektórych z
tych liczb. Pokażemy też dokładnie, jak taki rozkład
można znaleźć.
Algorytm, który mamy na myśli, można odczytać z dowodu
następującego twierdzenia ogólnego, udowodnionego w 1949
roku przez H. E. Richerta.
Twierdzenie. Każda liczba naturalna  jest
sumą różnych nieparzystych liczb pierwszych.
jest
sumą różnych nieparzystych liczb pierwszych.
Dowód. Najpierw przedstawimy każdą liczbą naturalną n spełniającą nierówności
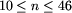

Tych liczb jest 37. Wybieramy teraz największą liczbę
pierwszą nie większą od 37. Będzie to sama liczba 37.
Teraz do każdego z otrzymanych 37 rozkładów dołączamy
liczbę 37. W ten sposób otrzymamy rozkłady liczb od
10+37=47 do 46+37=83 na sumy różnych nieparzystych
liczb pierwszych. Łącznie z otrzymanymi wcześniej
rozkładami mamy teraz rozkłady 74 liczb: od 10 do 83.
Wybieramy następną liczbę pierwszą: będzie to
największa liczba pierwsza nie większa od 74; w naszym
przypadku jest to liczba 73. Dołączamy tę liczbę do
każdego z dotychczasowych rozkładów, otrzymując w ten
sposób rozkłady wszystkich liczb aż do 83+73=156. Mamy
więc rozkłady 147 liczb od 10 do 156.
Wybieramy tym razem największą liczbę pierwszą nie
większą od 147, dołączamy ją do znalezionych
rozkładów i tak dalej.
Jest to bardzo naturalna metoda postępowania. Powstaje
jednak pytanie, czy jest ona zawsze skuteczna. Mianowicie
mogłoby się okazać, że kolejna wybrana liczba pierwsza
(pamiętamy: wybieramy największą liczbę nie większą
od liczby tych liczb, dla których już znaleźliśmy
rozkład) jest równa poprzednio wybranej liczbie
pierwszej. Inaczej mówiąc, mogłoby się okazać, że za
ostatnio wybraną liczbą pierwszą występuje tak wiele
liczb złożonych, że nie możemy dobrać odpowiednio
kolejnej liczby pierwszej. Okazuje się jednak, że tak nie
jest i można tego dowieść. Dowód wymaga jednak
skorzystania z bardzo znanego twierdzenia z teorii liczb,
tzw. twierdzenia Czebyszewa, które zapewne nie jest znane
większości uczniów liceum. W naszym zadaniu jednak
dowód twierdzenia nie jest potrzebny. Wystarczy bowiem
sprawdzić, że taką liczbę można dobrać zawsze do
momentu, gdy uzyskamy rozkłady wszystkich liczb nie
większych od 2 miliardów. Przykłady takich liczb
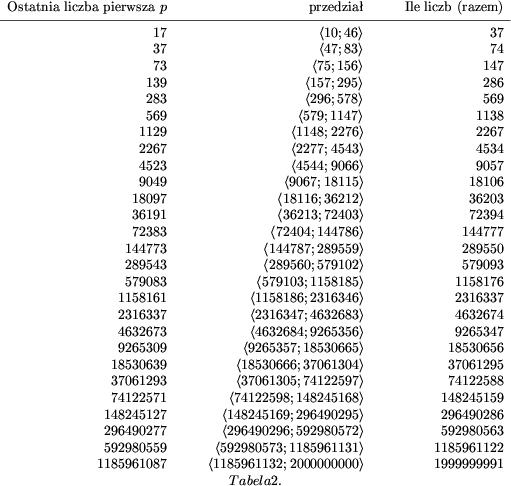
pierwszych zawarte są w tabeli 2.
W kolumnie pierwszej podajemy największą dotychczas
użytą liczbę pierwszą p. W kolumnie drugiej podajemy
przedział liczb, w którym ta liczba p jest użyta jako
największa liczba rozkładu (z wyjątkiem pierwszego
wiersza). Wreszcie w kolumnie trzeciej podajemy, ile liczb
ma już znany rozkład (od 10 do największej liczby, dla
której mamy znaleziony rozkład). Ta liczba jest o 9
mniejsza od największej liczby, dla której znamy
rozkład.
Zwróćmy jeszcze uwagę na to, że w pierwszym wierszu
występuje liczba pierwsza 17 jako największa liczba
występująca w rozkładach liczb od 10 do 46. To nie
znaczy oczywiście, że występuje ona w każdym z tych
rozkładów. Rozkłady liczb od 10 do 46 muszą być brane
z tabeli pierwszej.
Teraz już można łatwo napisać algorytm:
 .
.
Dopóki n>46 powtarzaj
Znajdź w drugiej kolumnie przedział, do którego należy n.
Zapamiętaj odpowiadającą mu liczbę p z pierwszej kolumny.
n:=n-p.
Teraz już  .
.
Zapamiętaj znajdujące się w tabeli pierwszej liczby pierwsze występujące w rozkładzie n.
Zapamiętane liczby wypisz w kolejności rosnącej.
Powróćmy teraz do dowodu twierdzenia. Oznaczmy przez p
największą użytą liczbę pierwszą i przez M
największą liczbę, dla której znaleźliśmy rozkład.
Niech k będzie liczbą tych liczb, dla których taki
rozkład znaleźliśmy. Oczywiście wtedy k=M-9.
Na początku mamy p=17, M=46 i k=37. Zauważmy, że
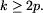
Niech teraz q będzie największą liczbą pierwszą
nie większą od k. Wtedy q>p. Wynika to ze znanego
twierdzenia Czebyszewa:
Twierdzenie. Dla każdej liczby naturalnej 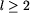 istnieje liczba pierwsza r taka, że l<r<2l.
istnieje liczba pierwsza r taka, że l<r<2l.
Dowód twierdzenia Czebyszewa można znaleźć np. w książkach W. Sierpińskiego Arytmetyka teoretyczna lub Teoria liczb, t. II. Z twierdzenia Czebyszewa wynika, że istnieje nieparzysta liczba pierwsza r taka, że:
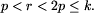
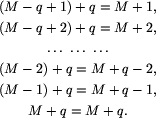
Połóżmy teraz
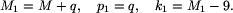
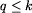 , więc
, więc
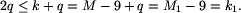
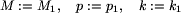
 . Możemy więc
powtórzyć postępowanie itd.
. Możemy więc
powtórzyć postępowanie itd.
Ponieważ M1>M, więc za każdym razem dostajemy
rozkład co najmniej jednej nowej liczby na sumę różnych
nieparzystych liczb pierwszych, co dowodzi, że każda
liczba  ma taki rozkład. To kończy dowód
twierdzenia Richerta.
ma taki rozkład. To kończy dowód
twierdzenia Richerta.
Można podać wiele innych algorytmów rozwiązujących to
zadanie. Najprostszy polega na wybieraniu największej
liczby pierwszej p nie większej od n i następnie
rozwiązaniu zadania dla liczby n-p zamiast n. Ten
algorytm nie zawsze prowadzi do sukcesu. Jeśli np. n=27,
to wybierzemy liczbę p=23 i wtedy zadanie nie ma
rozwiązania dla n-p=4. Możemy jednak próbować zadbać
o to, by otrzymana różnica była co najmniej równa 10:
wtedy zadanie dla n-p będzie miało rozwiązanie. To
daje bardzo prosty algorytm:
Dana jest liczba  .
.
Dopóki  powtarzaj
powtarzaj
Znajdź liczbę pierwszą p taką, że
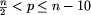 .
.
Zapamiętaj liczbę p.
n:=n-p.
Zapamiętane liczby pierwsze wypisz w
kolejności rosnącej.
Warunek 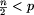 gwarantuje, że kolejno znajdowane
liczby pierwsze będą różne. Mamy bowiem wtedy
gwarantuje, że kolejno znajdowane
liczby pierwsze będą różne. Mamy bowiem wtedy
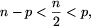
Ten algorytm jednak nie jest poprawny, gdyż nie dla każdej liczby n istnieje liczba pierwsza p taka, że
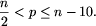
Twierdzenie. Jeśli  , to w przedziale
, to w przedziale
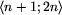 istnieje co najmniej 5 liczb
pierwszych.
istnieje co najmniej 5 liczb
pierwszych.
Z tego twierdzenia wynika łatwo następujący wniosek:
Wniosek. Jeśli n>26, to istnieje liczba pierwsza p taka, że
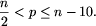
Zauważmy, że z tego wniosku wynika natychmiast inny
dowód twierdzenia Richerta. Przeprowadzenie tego dowodu
pozostawimy jako ćwiczenie dla Czytelnika. Możemy też
zmodyfikować algorytm, tak by działał poprawnie dla
wszystkich n:
Dana jest liczba  .
.
Dopóki n>26 powtarzaj
Znajdź liczbę pierwszą p taką, że
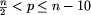 .
.
Zapamiętaj liczbę p.
n:=n-p
Teraz już 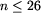 .
.
Zapamiętaj znajdujące się w tabeli pierwszej liczby pierwsze występujące
w rozkładzie n.
Zapamiętane liczby pierwsze wypisz w
kolejności rosnącej.
Ten algorytm może jednak działać dość długo. Liczby
p najlepiej szukać ,,od góry'': po odjęciu liczby p
od n dostaniemy liczbę dość małą i teraz już szybko
znajdziemy rozkład tej liczby na sumę różnych liczb
pierwszych. Warto jednak odnotować fakt, że znane są
długie ciągi kolejnych liczb złożonych, tzw. luki.
Luka długości k oznacza, że po liczbie pierwszej p,
liczby p+1, ..., p+k-1 są złożone i dopiero liczba
p+k jest pierwsza. Oczywiście długości luk muszą być
liczbami parzystymi. Znane są luki do długości 778 (dla
liczb pierwszych p<72635119999997) i niektóre inne. To
oznacza, że poszukiwanie największej liczby pierwszej nie
większej od n-10 może potrwać dość długo, tym
bardziej, że sprawdzanie, czy dana liczba jest pierwsza,
też jest czasochłonne.
Najniżej występującą luką długości 100 jest luka
między liczbami pierwszymi 396733 i 396833. Ale istnieją
większe luki. Najdłuższa znana ma długość 863:
Po liczbie 6 505 941 701 960 039 występują 863 liczby
złożone. Ta liczba jest większa od 2 miliardów, ale na
przykład po liczbie 166726367 występują 194 liczby
złożone. J. Young i A. Potler opublikowali (First
occurrence of prime gaps, Math. Comp., 1989,
52, 221-224) tablicę takich luk. Niektóre testy
zostały dobrane w taki sposób, by poszukiwanie liczby
pierwszej p trwało długo; do tego celu została
wykorzystana wspomniana tabela luk (użyto luk długości
do 300).
Można jednak zauważyć, że znaleziona liczba pierwsza p jest ,,dobra'' dla wielu liczb n; dokładniej dla liczb n spełniających nierówności

Do sprawdzenia rozwiązań użyto 11 testów. Test GOL0.IN to test z treści zadania. Następne trzy testy to testy poprawnościowe (odpowiednio dla małych, średniej wielkości i dużych liczb). Następne testy sprawdzały szybkość działania programu i wykorzystywały wspomniane wcześniej luki. Te testy różniły się między sobą wielkością liczb i usytuowaniem luki po to, by sprawdzić różne sposoby szukania liczby pierwszej p mniejszej od n-10.