Jeśli zbiór Wymuś(X) jest pułapką dla Bolka, to Ania ma
strategię wygrywającą z każdego pola w zbiorze Wymuś(X).
Dowód.
Rozważmy następującą strategię dla Ani:
- w każdym białym polu Ani ze zbioru Wymuś(X), Ania gra
zgodnie z jej strategią wygrywającą w uproszczonej grze w
zielone;
- w każdym zielonym polu Ani ze zbioru Wymuś(X), tj. w
każdym polu Ani ze zbioru X, Ania wybiera następnika który
należy do zbioru Wymuś(X):
taki następnik istnieje, bo zbiór Wymuś(X) jest pułapką
dla Bolka.
Zauważ, że w każdej rozgrywce zgodnej z tą strategią, pionek nigdy
nie opuszcza zbioru Wymuś(X).
Co więcej, żaden cykl
(tj. fragment rozgrywki rozpoczynający się i kończący w tym samym
polu)
w takiej rozgrywce nie składa się tylko z
białych pól, ponieważ strategia Ani na białych polach jest
wygrywająca w uproszczonej grze w zielone.
Dlatego każda rozgrywka zgodna z powyższą strategią jest
wygrywająca dla Ani w zwyczajnej grze w zielone.

Pozostaje nam do rozwiązania sytuacja, w której zbiór
Wymuś(Z) nie jest pułapką dla Bolka.
Niech  będzie zbiorem zielonych pól, które
spełniają warunki [5]lub [6] definicji pułapki dla Bolka, dla
X = Z.
będzie zbiorem zielonych pól, które
spełniają warunki [5]lub [6] definicji pułapki dla Bolka, dla
X = Z.
Zauważ, że w zielonych polach nie należących do zbioru Z1, Bolek
ma następującą strategię wygrywającą:
najpierw przesuń pionek w jednym kroku do pola nie należącego do
zbioru Wymuś(Z), a następnie użyj strategii wygrywającej
zagwarantowanej przez
Fakt [2].
Możemy zatem odrzucić zielone pola spoza zbioru Z1, jako
``bezużyteczne'' dla Ani.
Aby ponowić próbę użycia
Faktu [8] do wyznaczenia
strategii wygrywającej dla Ani, rozważmy zbiór
Wymuś(Z1).
Jeśli ten zbiór jest pułapką dla Bolka, to rozwiązanie gry w
zielone jest gotowe
(można wykazać - patrz dowód ogólniejszego
Faktu []
poniżej - że także we wszystkich białych polach spoza zbioru
Wymuś(Z1) Bolek ma strategię wygrywającą.)
W przeciwnym wypadku należy ponownie odrzucić zielone pola, które
okazały się bezużyteczne dla Ani, itd.
Powyższe rozumowanie motywuje następującą metodę obliczania
kolejnych, coraz mniejszych zbiorów zielonych pól, które kandydują
do roli pól dających Ani strategię wygrywającą (poprzez
Fakt [8]).
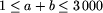 .
W kolejnych a+b wierszach opisano pola planszy - najpierw pola należące
do Ani, a następnie pola należące do Bolka.
Wiersz o numerze i+1, dla
.
W kolejnych a+b wierszach opisano pola planszy - najpierw pola należące
do Ani, a następnie pola należące do Bolka.
Wiersz o numerze i+1, dla 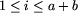 , zawiera na początku
liczby całkowite z, k oddzielone pojedynczym odstępem, oznaczające
odpowiednio kolor pola o numerze i (0 oznacza kolor biały,
1 - kolor zielony), oraz liczbę
następników tego pola. Następnie w tym wierszu zapisane jest
k liczb całkowitych (
, zawiera na początku
liczby całkowite z, k oddzielone pojedynczym odstępem, oznaczające
odpowiednio kolor pola o numerze i (0 oznacza kolor biały,
1 - kolor zielony), oraz liczbę
następników tego pola. Następnie w tym wierszu zapisane jest
k liczb całkowitych (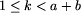 ),
pooddzielanych pojedynczymi odstępami,
będącymi numerami następników danego pola.
Liczba pól zielonych na planszy nie przekracza 100.
Suma liczb następników wszystkich pól na planszy nie przekracza 30 000.
),
pooddzielanych pojedynczymi odstępami,
będącymi numerami następników danego pola.
Liczba pól zielonych na planszy nie przekracza 100.
Suma liczb następników wszystkich pól na planszy nie przekracza 30 000.
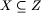 będzie pewnym zbiorem zielonych pól na
planszy.
Uproszczona gra w zielone toczy się w sposób podobny do
zwyczajnej gry w zielone.
Różnica polega na tym, że w uproszczonej grze w zielone rozgrywka
może się zakończyć wcześniej:
gdy pionek odwiedzi zielone pole ze zbioru X po raz pierwszy,
rozgrywka zostaje przerwana i Ania zwycięża.
będzie pewnym zbiorem zielonych pól na
planszy.
Uproszczona gra w zielone toczy się w sposób podobny do
zwyczajnej gry w zielone.
Różnica polega na tym, że w uproszczonej grze w zielone rozgrywka
może się zakończyć wcześniej:
gdy pionek odwiedzi zielone pole ze zbioru X po raz pierwszy,
rozgrywka zostaje przerwana i Ania zwycięża.

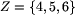 oraz
Wymuś
oraz
Wymuś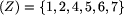 .
W polach spoza zbioru Wymuś(Z), tj. w polach ze zbioru
.
W polach spoza zbioru Wymuś(Z), tj. w polach ze zbioru
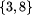 , Bolek ma strategię wygrywającą polegającą na
wybraniu pola 3 jako następnika w polu 8.
, Bolek ma strategię wygrywającą polegającą na
wybraniu pola 3 jako następnika w polu 8.
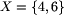 .
Zbiór Wymuś
.
Zbiór Wymuś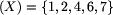 jest pułapką dla Bolka,
ponieważ:
jest pułapką dla Bolka,
ponieważ:
 będzie zbiorem zielonych pól, które
spełniają warunki
będzie zbiorem zielonych pól, które
spełniają warunki 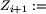 zbiór pól z Zi spełniających warunki~\ref{definicja:pulapka-1}\ lub~\ref{definicja:pulapka-2}\ definicji~\ref{definicja:pulapka-dla-bolka}
zbiór pól z Zi spełniających warunki~\ref{definicja:pulapka-1}\ lub~\ref{definicja:pulapka-2}\ definicji~\ref{definicja:pulapka-dla-bolka}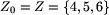 oraz
Wymuś
oraz
Wymuś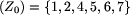 .
Zauważ, że Z0 nie jest pułapką dla Bolka, bo pole 5 należy do
Ani, ale jedyny następnik pola 5, tj. pole 8, nie należy do
zbioru Wymuś(Z0).
Pole 5 jest jedynym polem z Z0 nie spełniającym
warunków [5] lub [6] definicji [4], więc
.
Zauważ, że Z0 nie jest pułapką dla Bolka, bo pole 5 należy do
Ani, ale jedyny następnik pola 5, tj. pole 8, nie należy do
zbioru Wymuś(Z0).
Pole 5 jest jedynym polem z Z0 nie spełniającym
warunków [5] lub [6] definicji [4], więc
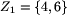 .
Z przykładu [7] wiemy, że zbiór
Wymuś(Z1) jest pułapką dla Bolka.
.
Z przykładu [7] wiemy, że zbiór
Wymuś(Z1) jest pułapką dla Bolka.
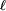 będzie najmniejszą liczbą dla której zbiór
Wymuś
będzie najmniejszą liczbą dla której zbiór
Wymuś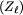 jest pułapką dla Bolka.
Oczywiście Ania ma strategię wygrywającą ze zbioru
Wymuś
jest pułapką dla Bolka.
Oczywiście Ania ma strategię wygrywającą ze zbioru
Wymuś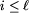 , Bolek ma strategię wygrywającą z
każdego pola spoza zbioru Wymuś(Zi).
, Bolek ma strategię wygrywającą z
każdego pola spoza zbioru Wymuś(Zi).
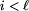 , Bolek ma strategię
wygrywającą z każdego pola spoza zbioru Wymuś(Zi).
Wykażemy, że wtedy Bolek ma także strategię wygrywającą z
każdego pola spoza zbioru Wymuś
, Bolek ma strategię
wygrywającą z każdego pola spoza zbioru Wymuś(Zi).
Wykażemy, że wtedy Bolek ma także strategię wygrywającą z
każdego pola spoza zbioru Wymuś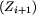 .
.
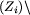 Wymuś
Wymuś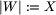
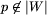 takie, że \emph{AniaWymusza}(W, p) do
takie, że \emph{AniaWymusza}(W, p) do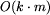 , gdzie k jest liczbą zielonych pól, a m jest
sumą liczb następników dla wszystkich pól.
, gdzie k jest liczbą zielonych pól, a m jest
sumą liczb następników dla wszystkich pól.
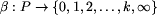 :
z każdym polem
:
z każdym polem 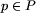 , związana jest etykieta
, związana jest etykieta 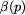 ,
która jest liczbą naturalną nie większą niż k, lub symbolem
,
która jest liczbą naturalną nie większą niż k, lub symbolem
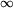 .
Przyjmujemy umownie, że
.
Przyjmujemy umownie, że 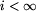 , dla każdej liczby
naturalnej i.
Powiemy, że etykietowanie
, dla każdej liczby
naturalnej i.
Powiemy, że etykietowanie 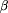 jest
dobre dla Bolka w polu p,
jeśli
jest
dobre dla Bolka w polu p,
jeśli 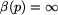 lub spełnione są następujące
warunki:
lub spełnione są następujące
warunki:
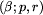 ;
;
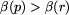 , jeśli pole p jest zielone, oraz
, jeśli pole p jest zielone, oraz
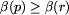 , jeśli pole p jest białe.
, jeśli pole p jest białe.
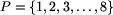 .
Niech etykietowanie
.
Niech etykietowanie 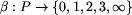 będzie
zdefiniowane przez następującą tabelę.
będzie
zdefiniowane przez następującą tabelę.

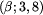 , tj.
, tj. 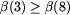 ;
zauważ, że wystarczy tu nieostra nierówność, bo pole 3 jest
białe;
;
zauważ, że wystarczy tu nieostra nierówność, bo pole 3 jest
białe;
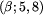 , tj.
, tj. 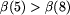 ;
zauważ, że wymagana tu jest ostra nierówność, bo pole 5 jest
zielone;
;
zauważ, że wymagana tu jest ostra nierówność, bo pole 5 jest
zielone;
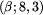 , tj.
, tj. 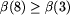 .
.
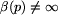 .
.
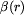 .
Zauważmy, że z definicji dobrego etykietowania dla Bolka wynika, że
wtedy dla każdej rozgrywki p1, p2, p3, ..., pi mamy
.
Zauważmy, że z definicji dobrego etykietowania dla Bolka wynika, że
wtedy dla każdej rozgrywki p1, p2, p3, ..., pi mamy
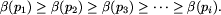
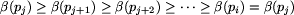 ,
więc musi być
,
więc musi być
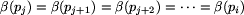 .
Z definicji dobrego etykietowania dla Bolka - a dokładniej z
punktu 1 definicji warunku
PostępBolka
.
Z definicji dobrego etykietowania dla Bolka - a dokładniej z
punktu 1 definicji warunku
PostępBolka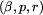 - wynika, że pola
- wynika, że pola
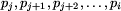 są białe.
Inaczej mówiąc, żadne pole odwiedzone pomiędzy pierwszą i drugą
wizytą w polu pj = pi nie jest zielone, czyli rozgrywka jest
wygrywająca dla Bolka.
są białe.
Inaczej mówiąc, żadne pole odwiedzone pomiędzy pierwszą i drugą
wizytą w polu pj = pi nie jest zielone, czyli rozgrywka jest
wygrywająca dla Bolka.
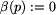
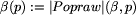
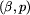 to najmniejsza etykieta nie mniejsza
od
to najmniejsza etykieta nie mniejsza
od 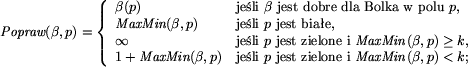
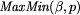 jest zdefiniowane w następujący
sposób:
jest zdefiniowane w następujący
sposób:
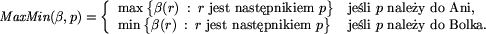
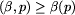 oraz, że
Popraw
oraz, że
Popraw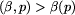 , jeśli etykietowanie
, jeśli etykietowanie 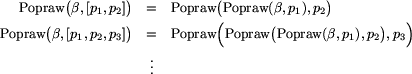 Rozważmy następujące wykonanie procedury PodnośEtykietowanie:
Rozważmy następujące wykonanie procedury PodnośEtykietowanie:
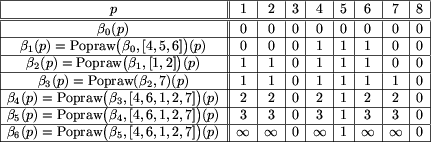
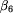 jest dobre dla Bolka.
Zauważ, że etykietowanie
jest dobre dla Bolka.
Zauważ, że etykietowanie 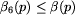 .
.
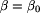 , gdzie
, gdzie
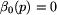 , dla każdego pola p, jest ,,mniejsze'' niż
jakiekolwiek inne etykietowanie.
(Dla ścisłości, mówimy, że etykietowanie
, dla każdego pola p, jest ,,mniejsze'' niż
jakiekolwiek inne etykietowanie.
(Dla ścisłości, mówimy, że etykietowanie 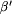 , jeśli
, jeśli
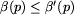 , dla każdego pola p.)
Kolejne ,,poprawki'' polegające na podnoszeniu wartości
etykietowania
, dla każdego pola p.)
Kolejne ,,poprawki'' polegające na podnoszeniu wartości
etykietowania 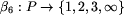 :
:

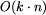 .
.
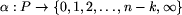 .
Powiemy, że etykietowanie
.
Powiemy, że etykietowanie  jest
dobre dla Ani w polu p, jeśli
jest
dobre dla Ani w polu p, jeśli 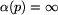 lub
spełnione są następujące warunki:
lub
spełnione są następujące warunki:
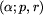 ,
,
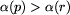 , jeśli pole p jest białe.
Mówimy, że etykietowanie
, jeśli pole p jest białe.
Mówimy, że etykietowanie 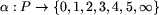 zdefiniowane przez następującą tabelę jest dobre dla Ani.
zdefiniowane przez następującą tabelę jest dobre dla Ani.

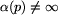 .
.
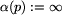 end
end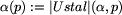
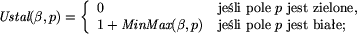
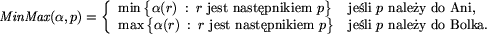
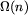 .
Czy istnieje algorytm rozwiązujący gry w zielone działający w
czasie
.
Czy istnieje algorytm rozwiązujący gry w zielone działający w
czasie 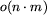 ?
W szczególności, czy istnieje algorytm rozwiązujący gry w
zielone działający w czasie O(m)?
?
W szczególności, czy istnieje algorytm rozwiązujący gry w
zielone działający w czasie O(m)?