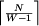rundach (zaokrąlenie w górę).
Minimalna liczba rund nigdy nie jest większa niż
.
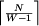| Krzysztof Diks, Marcin Kubica |
| Tłumaczenie |
Na centralnym parkingu pod Wielkim Murem znajduje się długi rząd miejsc parkingowych. Jeden z końców tego rzędu uważa się za lewy, a drugi za prawy. Cały rząd jest wypełniony parkującymi samochodami. Każdy samochód jest ustalonej marki, ale może być wiele samochodów tej samej marki. Marki identyfikujemy liczbami całkowitymi. Pracownicy parkingu postanowili ustawić auta w niemalejącej kolejności względem ich marek, od lewego do prawego końca. Do tego celu wykorzystają następującą metodę postępowania. W tak zwanej rundzie, każdy z pracowników może wyjechać jednym samochodem z miejsca jego postoju (pracownicy pracują jednocześnie), a następnie zaparkować na zwolnionym w tej samej rundzie miejscu postojowym. Może się zdarzyć, że w danej rundzie nie wszyscy pracują. Oczywiście, pracownicy chcieliby wykonać swoją pracę w jak najmniejszej liczbie rund.
Niech N będzie liczbą samochodów, a W liczbą pracowników parkingu. Napisz
program, który dla danej liczby marek samochodów na parkingu i danej liczby
pracowników, znajduje sposób uporządkowania samochodów w co najwyżej
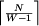rundach (zaokrąlenie w górę).
Minimalna liczba rund nigdy nie jest większa niż
.
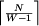Rozważmy następujący przykład. Na parkingu znajduje się 10 samochodów o markach 1, 2, 3 i 4, oraz 4 pracowników. Na poczatku kolejność samochodów na parkingu, od lewej do prawej i względem ich marek, jest taka: 2 3 3 4 4 2 1 1 3 1. Minimalna liczba rund wynosi 3, a rundy można wykonać w taki sposób, że rozmieszczenie samochodów po każdej z nich jest następujące:
Nazwą pliku wejściowego jest CAR.IN. Pierwszy wiersz pliku wejściowego
zawiera trzy liczby całkowite.
Pierwszą liczbą jest N - liczba samochodów na parkingu,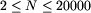 
.
Drugą liczbą jest liczba marek M,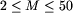 
. Marki są ponumerowane od 1
do M. Na parkingu znajduje sie co najmniej jeden samochód każdej marki.
Trzecia liczba jest liczbą pracowników parkingu W,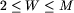 
.
Drugi wiersz zawiera N liczb całkowitych - i-ta liczba jest marką i-tego
samochodu w rzędzie, patrząc od lewego do prawgo końca.
Nazwą pliku wyjsciowego jest CAR.OUT. Pierwszy wiersz pliku wyjściowego powinien zawierać jedną liczbę całkowitą R - liczbę rund w znalezionym rozwiązaniu. Kolejne R wierszy zawiera opisy kolejnych rund od 1 do R. Każdy taki wiersz rozpoczyna się od liczby całkowitej C - liczby samochodów, które należy ruszyć w tej rundzie. Następnie pojawia się 2C liczb całkowitych - identyfikatorów pozycji samochodów. Pozycje samochodów są ponumerowane od lewego do prawego końca, kolejnymi liczbami 1,2,... N. Pierwsze dwie liczby tworzą parę opisującą ruch jednego z samochodów: pierwsza liczba jest pozycją tego samochodu (od lewego końca) sprzed opisywanej rundy, a druga liczba jest pozycją tego samochodu (od lewego końca) po tej rundzie. Trzecia i czwarta liczba tworzą parę opisującą ruch innego samochodu, itd. Dla każdego z tych R wierszy może być wiele różnych rozwiązań, ale Twój program powinien wypisać tylko jedno z nich.
CAR.IN:
10 4 4 2 3 3 4 4 2 1 1 3 1
CAR.OUT:
3 4 2 7 3 8 7 2 8 3 3 4 9 9 6 6 4 3 1 5 5 10 10 1
Przypuśćmy, że twój program wypisał liczę rund R, a 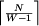jest równe Q.
Jeśli twój program wypisuje niepoprawne opisy rund lub w wyniku ich wykonania
samochody nie zostaną uporządkowane, nie zdobywasz żadnych punktów. W
przeciwnym przypadku otrzymasz liczbę punktów obliczoną w następujący sposób:
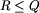- 100\% punktów
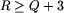- 0\% punktów