Krzysztof Diks, Marcin Kubica

Tłumaczenie

Walls

Zadanie

W pewnym kraju, wielkie mury pobudowano w taki sposób, że każdy z nich łączy dokładnie dwa miasta. Wielkie mury nie przecinają się wzajemnie. W ten sposób kraj został podzielony na obszary i żeby przejechać z jednego obszaru na inny, trzeba przedostać się przez mur łączący te obszary. Ponadto można przejść z miasta A do B idąc tylko przez miasta i po murach. Pewne dodatkowe ograniczenia wynikają z formatu danych wejściowych.

W opisywanym kraju działa klub podróżnika, którego członkowie żyją w miastach - w każdym mieście co najwyżej jeden członek. Od czasu do czasu członkowie klubu podróżują rowerami i unikają przejazdów przez miasta, ponieważ nie lubią spalin i korków ulicznych. Ponieważ pokonywanie murów z rowerem jest bardzo niewygodne, starają się wybrać tak obszar spotkania, żeby pokonać jak najmniej murów. Aby dostać się na spotkanie każdy z nich musi pokonać pewną liczbę (możliwe, że 0) murów. Chcą więc znaleźć taki obszar, który zminimalizuje sumaryczną liczbę pokonywanych przez nich murów (zwaną w skrócie liczbą pokonywanych murów). Taki obszar nazwiemy obszarem optymalnym.

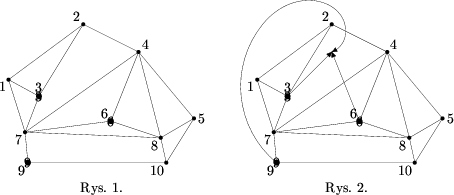
Miasta są ponumerowane od 1 do N, gdzie N jest liczbą miast. Na rysunku 1 miasta są przedstawione jako ponumerowane węzły, a odcinki łączące węzły symbolizują mury. Przypuśćmy, że klub podróżnika ma 3 członków, którzy mieszkają w miastach 3,6 i 9. Na rysunku 2 zaznaczono optymalny obszar i drogę podróżników dla danych z rysunku 1. Liczba pokonywanych murów wynosi 2: podróżnik z miasta 9 pokonuje mur łączący miasta 2 i 4, a podróżnik z miasta 6 pokonuje mur łączący miasta 4 i 7.

Napisz program, który dla danych miast, obszarów i miejsca zamieszkania członków klubu, obliczy pewien optymalny obszar i minimalną liczbę murów pokonywanych przez członków klubu.

Wejście

Nazwą pliku wejściowego jest WALLS.IN. Pierwszy wiersz zawiera jedną liczbę całkowitą: liczbę obszarów M, 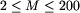. Drugi wiersz zawiera jedną liczbę całkowitą: liczbę miast N, 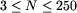. Trzeci wiersz zawiera liczbę członków klubu L, 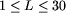, 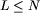. Czwarty wiersz zawiera L różnych liczb całkowitych uporządkowanych rosnąco: numery miast, w których mieszkają członkowie klubu.

Kolejne 2M wierszy zawiera opisy obszarów - po dwa wiersze na obszar. Pierwsze dwa wiersze opisują pierwszy obszar, następne dwa opisują drugi obszar, itd. W każdej takiej parze wierszy, pierwszy z nich zawiera liczbę całkowitą I, równą liczbie miast na granicy opisywanego obszaru. Drugi wiersz zawiera numery I miast na granicy opisywanego obszaru, podane kolejno w porządku zgodnym z ruchem wskazówek zegara. Wyjątkiem jest obszar zewnętrzny (nieograniczony) opisywany jako ostatni. Wierzchołki na granicy tego obszaru są podane w kierunku przeciwnym do ruchu wskazówek zegara. Obszary są ponumerowane od 1 do M, w kolejności ich opisów w pliku wejściowym. Pamiętaj, że plik wejściowy zawiera opisy wszystkich obszarów, również obszaru zewnętrznego.

Wyjście

Nazwą pliku wyjściowego jest WALLS.OUT. Pierwszy wiersz zawiera jedną liczbę całkowitą: minimalną liczbę przekraczanych w sumie murów. Drugi wiersz zawiera jedną liczbę całkowitą: numer optymalnego obszaru spotkania. Może istnieć wiele takich obszarów i Twój program powinien wypisać numer tylko jednego z nich.

Przykład

Podane poniżej pliki, wejściowy i wyjściowy, odpowiadają przykładowi podanemu w tekście:

10
10
3
3 6 9
3
1 2 3
3
1 3 7 
4 
2 4 7 3
3 
4 6 7 
3 
4 8 6
3
6 8 7
3

4 5 8
4
7 8 10 9
3
5 10 8
7
7 9 10 5 4 2 1

2
3