1 2 12 0 0 1 1 2 2 3 3 4 5 5 5 4 2 1 4 0 5 5 0 2 3 3 2
| Tomasz Waleń | Marcin Sawicki |
| Treść zadania, Opracowanie | Program wzorcowy |
Bajtazar, zasłużony pracownik Bajtockiej Kopalni Złota, przechodzi w tym roku na emeryturę. W związku z tym, zarząd kopalni postanowił go uhonorować. W nagrodę za wieloletnią pracę, Bajtazar może otrzymać działkę - wycinek kopalni mający postać prostokąta o bokach równoległych do osi współrzędnych oraz szerokości s i wysokości w - położoną w dowolnie przez siebie wybranym miejscu. Oczywiście nie wszystkie lokalizacje działki są równie cenne. Wartość działki mierzy się liczbą samorodków złota znajdujących się na jej terenie (jeśli samorodek leży na granicy działki, to również znajduje się na jej terenie).
Twoim zadaniem jest napisanie programu umożliwiającego wyznaczenie jaką wartość ma najcenniejsza spośród wszystkich możliwych lokalizacji działek.
Dla uproszczenia przyjmujemy, że teren kopalni jest nieograniczony, jakkolwiek samorodki występują jedynie na ograniczonym obszarze.
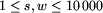 ), oznaczające odpowiednio
szerokość i wysokość działki.
W drugim wierszu zapisano jedną dodatnią liczbę
całkowitą n (
), oznaczające odpowiednio
szerokość i wysokość działki.
W drugim wierszu zapisano jedną dodatnią liczbę
całkowitą n (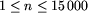 ), oznaczającą liczbę samorodków
znajdujących się na terenie kopalni.
W kolejnych n wierszach zapisane są współrzędne poszczególnych
samorodków.
Każdy z tych wierszy zawiera dwie liczby całkowite x i y
(
), oznaczającą liczbę samorodków
znajdujących się na terenie kopalni.
W kolejnych n wierszach zapisane są współrzędne poszczególnych
samorodków.
Każdy z tych wierszy zawiera dwie liczby całkowite x i y
(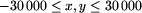 ), oddzielone pojedynczym odstępem,
oznaczające odpowiednio współrzędną x i y samorodka.
), oddzielone pojedynczym odstępem,
oznaczające odpowiednio współrzędną x i y samorodka.
1 2 12 0 0 1 1 2 2 3 3 4 5 5 5 4 2 1 4 0 5 5 0 2 3 3 2

poprawną odpowiedzią jest plik wyjściowy kop.out:
4
Najprostszym rozwiązaniem tego zadania jest sprawdzenie wartości
wszystkich możliwych działek, jednak z oczywistych powodów jest to rozwiązanie
bardzo nieefektywne. Co prawda możemy ograniczyć się do takich działek,
których wierzchołki pokrywają się z punktami kratowymi, ale nadal daje to
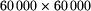 możliwości do sprawdzenia i co najgorsze, nawet w przypadku gdy ilość samorodków jest niewielka.
możliwości do sprawdzenia i co najgorsze, nawet w przypadku gdy ilość samorodków jest niewielka.
Do trochę lepszego rozwiązania prowadzi spostrzeżenie, iż zawsze możemy pokazać taką działkę o optymalnej wartości, na której lewym i dolnym brzegu leżą jakieś samorodki (każdą optymalną działkę można tak przesunąć by spełniała to kryterium, nie tracąc przy tym żadnych samorodków).
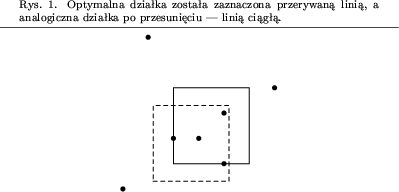
Zatem przestrzeń poszukiwań można już ograniczyć do O(n2) (na n różnych sposobów można wybrać samorodek na lewym brzegu i na n sposobów na dolnym brzegu), niestety nadal takie rozwiązanie będzie za mało efektywne w przypadku danych o dużych rozmiarach, ale dla danych o małych rozmiarach (np. prostych testów poprawnościowych) powinno być wystarczające.
Kod takiego rozwiązania może wyglądać następująco:
| 1 | rozw := 0; |
| 2 | for i := 1 to n do |
| 3 | for j := i to n do |
| 4 | begin |
| 5 | x := min(xi,xj); |
| 6 | y := min(yi,yj); |
| 7 | ile:= 0; |
| 8 | { policzenie ile samorodków znajduje się w obrębie prostokąta } |
| 9 | { (x,y)-(x+s,y+w) } |
| 10 | for k := 1 to n do |
| 11 | if (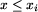 ) and ( ) and (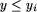 ) and ) and |
| 12 | (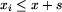 ) and ( ) and (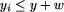 ) then inc(ile); ) then inc(ile); |
| 13 | if ile>rozw then rozw := ile |
| 14 | end |
Takie rozwiązanie ma złożoność O(n3),
co przy maksymalnych danych jakie mogą wystąpić w zadaniu oznacza
wykonanie około 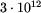 operacji.
Nawet przy założeniu, że dysponujemy szybkim komputerem, który potrafi wykonać
107 operacji w ciągu sekundy (jednak ta wartość jest bardzo uzależniona od
wybranego języka programowania, kompilatora czy nawet metody kompilacji), a sam
program przyspieszyć 3-krotnie (np. przez optymalizację), i tak oznaczałoby to,
że program potrzebowałby na znalezienie rozwiązania 100\,000s, czyli 27 godzin.
operacji.
Nawet przy założeniu, że dysponujemy szybkim komputerem, który potrafi wykonać
107 operacji w ciągu sekundy (jednak ta wartość jest bardzo uzależniona od
wybranego języka programowania, kompilatora czy nawet metody kompilacji), a sam
program przyspieszyć 3-krotnie (np. przez optymalizację), i tak oznaczałoby to,
że program potrzebowałby na znalezienie rozwiązania 100\,000s, czyli 27 godzin.
Jak więc ulepszyć poprzednie rozwiązanie? Można bardziej efektywnie
zliczać liczbę samorodków w obrębie danego prostokąta, korzystając z bardziej
zaawansowanych struktur danych, albo też można wykorzystać fakt, że wszystkie samorodki
mamy dane na samym początku i analizować je wg. jakiegoś porządku.
W rozwiązaniu wzorcowym użyto popularnej techniki zwanej zamiataniem.
Rozpatrzmy poziomą miotłę zamiatającą płaszczyznę od dołu do góry.
Dla danego położenia miotły będziemy chcieli
szybko obliczać wartości działek, których górny brzeg pokrywa się z
aktualnym położeniem miotły. Podczas zamiatania płaszczyzny, dla każdego
samorodka na miotle zaznaczamy przedział, w którym umieszczenie prawego
górnego rogu działki obejmuje ten samorodek. Konieczne jest również
dodanie sztucznych ``ujemnych'' samorodków, które będą służyły do usuwania
samorodka (gdy miotła oddali się na ogległość w).
Szkic takiego rozwiązania wygląda następująco:
| 1 | S := { (xi,yi,+1) oraz (xi,yi+w+1,-1): dla 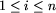 }; }; |
| 2 | rozw := 0; |
| 3 | przeglądaj S w kolejności rosnących współrzędnych y |
| 4 | (x,y,z) := { kolejny element z S }; |
| 5 | if z=+1 then |
| 6 | dodajPrzedział(x,x+s) |
| 7 | end |
| 8 | usunPrzedział(x,x+s); |
| 9 | rozw := max(rozw, MaksymalnyPrzedział); |
Funkcja MaksymalnyPrzedzial szuka punktu na osi X, który należy do największej liczby przedziałów i zwraca ich liczbę.
Dla danych z przykładu podanego w treści zadania zbiór S wygląda następująco:
Zbiór S przeglądamy zgodnie z rosnącą współrzędną y, jednak wszystkie dla tej samej współrzędnej y trójki ze znakiem -1 powinny znaleźć się przed tymi ze znakiem +1.
W naszym wypadku mogłaby to być kolejność:
Teraz pozostaje ustalić szczegóły: jakiej struktury danych użyć do reprezentowania przedziałów na miotle i jak szybko zrealizować funkcję MaksymalnyPrzedzial?
Odpowiedź na drugie pytanie można sprowadzić do problemu liczenia sum prefiksowych. Otóż gdy będziemy dodawać przedział [a,b], to należy na osi X na pozycji a dodać +1, a na pozycji b dodać -1. Gdy będziemy chcieli usunąć jakiś przedział należy postąpić odwrotnie: na pozycji a dodać -1, a na b dodać +1. Teraz aby sprawdzić do ilu przedziałów należy dany punkt p, wystarczy zsumować wartości od minimalnej wartości na osi X do p, natomiast obliczenie funkcji MaksymalnyPrzedzial odpowiada znalezieniu maksymalnej sumy prefiksowej. Metoda ta została zilustrowana na rysunku 2.
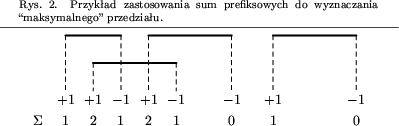
Bardzo często do reprezentowania miotły używa się drzew zrównoważonych takich jak AVL lub drzewa czerwono-czarne. Tak można postąpić i w tym wypadku, ale istnieje prostsze rozwiązanie. Ponieważ wszystkie punkty znamy zawczasu, możemy zbudować zrównoważone drzewo BST zawierające wszystkie wartości. Takie postępowanie może wydawać się trochę rozrzutne - w drzewach AVL przetrzymujemy tylko te wartości, które aktualnie są przetwarzane, a tu wszystkie. Jednak w tym wypadku punktów wcale nie jest aż tak dużo. Dodatkowo możemy takie drzewo ukryć w tablicy, dokładnie tak jak w przypadku kopców, a co za tym idzie, uniknąć dodatkowego kosztu związanego z przechowywaniem wskaźników, które definiują strukturę drzewa. Rysunek 3 pokazuje drzewo utworzone dla danych podanych w przykładzie zamieszczonym w treści zadania.
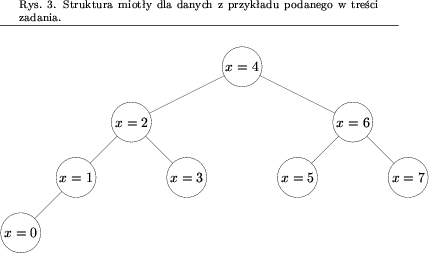
W każdym węźle drzewa oprócz wartości współrzędnej x (klucza) będziemy utrzymywać wartości:
Jak łatwo zauważyć, funkcja MaksymalnyPrzedzial sprowadza się do odczytania wartości pola MiotlaMaxSuma dla korzenia. Wstawianie wartości do miotły jest trochę bardziej kłopotliwe, należy bowiem aktualizować wszystkie te pola.
Dla danego klucza x i wartości w którą chcemy dodać, należy:
Przy aktualizowaniu pola MiotlaMaxSuma w węźle v mogą zajść dwa przypadki:
| 1 | procedure WstawDoMiotly(x, wartosc: Integer); |
| 2 | begin |
| 3 | { szukanie węzła z kluczem x } |
| 4 | Wezel := 1; |
| 5 | repeat |
| 6 | if x < MiotlaX[Wezel] then |
| 7 | Wezel := Wezel * 2 { idziemy do lewego poddrzewa } |
| 8 | end if x > MiotlaX[Wezel] then |
| 9 | Wezel := Wezel * 2 + 1 { idziemy do prawego poddrzewa } |
| 10 | end |
| 11 | break; |
| 12 | until false; |
| 13 | { Uaktualnianie sum na scieżce od Wezel do korzenia } |
| 14 | repeat |
| 15 | if Wezel * 2+1  IlePktowMiotly then begin IlePktowMiotly then begin |
| 16 | MaxSumaPrawa := MiotlaMaxSuma[Wezel * 2+1]; |
| 17 | SumaPrawa := MiotlaSuma[Wezel * 2+1]; |
| 18 | end end begin { jeśli brak prawego syna } |
| 19 | MaxSumaPrawa := 0; SumaPrawa := 0; |
| 20 | end; |
| 21 | |
| 22 | if Wezel * 2  IlePktowMiotly then IlePktowMiotly then |
| 23 | MaxSumaLewa := MiotlaMaxSuma[Wezel * 2]; |
| 24 | end { jeśli brak lewego syna } |
| 25 | MaxSumaLewa := 0; |
| 26 | |
| 27 | Inc(MiotlaSuma[Wezel], k); |
| 28 | MiotlaMaxSuma[Wezel] := max( |
| 29 | MaxSumaLewa, MiotlaSuma[Wezel]-SumaPrawa+MaxSumaPrawa); |
| 30 | Wezel := Wezel div 2 { przejście do ojca w drzewie } |
| 31 | |
| 32 | until Wezel = 0; |
| 33 | end |
Kod procedury realizującej dodawanie wartości do węzła drzewa wygląda następująco:
Teraz można wprowadzić zmodyfikowaną procedurę zamiatania:
| 1 | procedure Zamiataj; |
| 2 | begin |
| 3 | rozw := 0; |
| 4 | Q := { posortowane trójki wg. wsp. Y i znaku } |
| 5 | { przetwarzanie samorodków zgodnie z rosnącą wsp. Y } |
| 6 | while not empty Q do begin |
| 7 | (x,y,znak) := Q.extract; |
| 8 | WstawDoMiotly(x,y,znak); |
| 9 | WstawDoMiotly(x+szerokosc+1,y,-znak); |
| 10 | rozw := max(rozw,MiotlaMaxSuma[1]); |
| 11 | end |
| 12 | end |
Rysunek 4 przedstawia stan miotły po przetworzeniu 3 pierwszych samorodków.
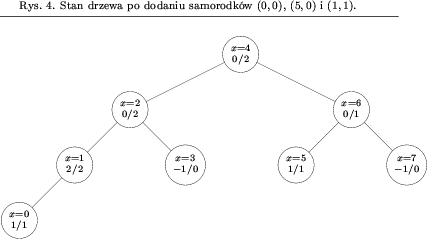
Podsumowując, aby otrzymać pełne rozwiązanie należy połączyć wszystkie wspomniane elementy:
| 1 | PrzygotujMiotle; |
| 2 | PosortujPunkty; |
| 3 | Zamiataj; |
Do wykonania każdego z tych kroków potrzeba czasu 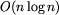 , stąd i
całe rozwiązanie ma taką złożoność.
, stąd i
całe rozwiązanie ma taką złożoność.
Rozwiązanie testowane było na 14 zestawach danych testowych, nie stosowano grupowania.