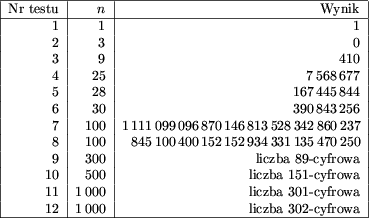
 ) są zdjęte z pręta, a ogniwo nr k jest
założone, to możemy zdjąć lub założyć ogniwo nr k+1.
) są zdjęte z pręta, a ogniwo nr k jest
założone, to możemy zdjąć lub założyć ogniwo nr k+1.
| Marcin Kubica | Paweł Wolff |
| Treść zadania, Opracowanie | Program wzorcowy |
Bajtocja nie zawsze była państwem demokratycznym.
W jej historii były również czarne karty.
Pewnego razu, generał Bajtelski -
przywódca junty żelazną ręką rządzącej Bajtocją -
postanowił zakończyć stan wojenny, trwający od momentu przejęcia
władzy, i zwolnić więzionych działaczy opozycji.
Nie chciał jednak uwolnić przywódcy opozycji Bajtazara.
Postanowił przykuć go do murów więzienia za pomocą
bajtockiego łańcucha.
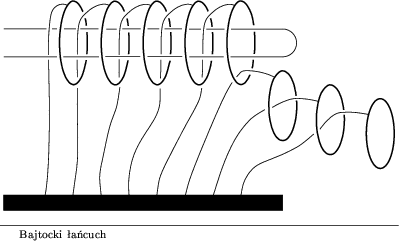
Bajtocki łańcuch składa się z połączonych ze sobą ogniw oraz
przymocowanego do muru pręta.
Choć ogniwa nie są połączone z prętem, to bardzo trudno jest
je z niego zdjąć.
- Generale, czemuś mnie przykuł do murów więzienia, miast
uwolnić, jako to uczyniłeś z moimi kamratami! - wołał
Bajtazar.
- Ależ Bajtazarze, wszak nie jesteś przykuty i z pewnością
potrafisz sam zdjąć trzymające Cię ogniwa z pręta wystającego
z murów więzienia. -
przewrotnie stwierdził generał Bajtelski, po czym dodał -
Uporaj się z tym jednak przed godziną cyfracyjną i nie dzwoń
łańcuchami po nocy, gdyż w przeciwnym przypadku będę zmuszony
wezwać funkcjonariuszy Cyfronicji Obywatelskiej.
Pomóż Bajtazarowi!
Ponumerujmy kolejne ogniwa łańcucha liczbami 1, 2, ..., n. Ogniwa te możemy zakładać i zdejmować z pręta zgodnie z następującymi zasadami:
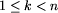 ) są zdjęte z pręta, a ogniwo nr k jest
założone, to możemy zdjąć lub założyć ogniwo nr k+1.
) są zdjęte z pręta, a ogniwo nr k jest
założone, to możemy zdjąć lub założyć ogniwo nr k+1.
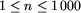 .
W drugim wierszu zapisano n liczb całkowitych
.
W drugim wierszu zapisano n liczb całkowitych
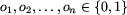 pooddzielanych pojedynczymi
odstępami.
Jeśli oi=1, to ogniwo nr i jest założone na pręt, a jeśli
oi=0, to jest z niego zdjęte.
pooddzielanych pojedynczymi
odstępami.
Jeśli oi=1, to ogniwo nr i jest założone na pręt, a jeśli
oi=0, to jest z niego zdjęte.
4 1 0 1 0poprawną odpowiedzią jest plik wyjściowy lan.out
6
Niech o = (o1, o2, ..., on) i o' = (o'1, o'2, ..., o'n) będą dowolnymi ciągami (tej samej długości) opisującymi stany bajtockiego łańcucha. Oznaczmy przez d(o, o') minimalną liczbę ruchów potrzebnych do przekształcenia łańcucha opisywanego przez o w łańcuch opisywany przez o'. Zadanie sprowadza się do wyznaczenia d(o, (0, 0, ..., 0)) dla o będącego ciągiem z pliku wejściowego. Zanim powiemy jak można obliczyć tę wartość, zastanówmy się nad ogólnymi własnościami funkcji d.
Zauważmy, że dla każdego ciągu o mamy d(o, o) = 0, gdyż nie
trzeba wykonywać żadnych ruchów, aby łańcuch pozostał bez zmian.
Oczywiście dla 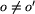 mamy d(o, o') > 0.
Zauważmy też, że ruchy jakie możemy wykonywać są symetryczne, a
więc dla dowolnych o i o' mamy d(o, o') = d(o', o).
Ponadto, dla dowolnych o, o' i o'' zachodzi nierówność
mamy d(o, o') > 0.
Zauważmy też, że ruchy jakie możemy wykonywać są symetryczne, a
więc dla dowolnych o i o' mamy d(o, o') = d(o', o).
Ponadto, dla dowolnych o, o' i o'' zachodzi nierówność
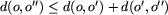 .
Jest tak dlatego, że d(o, o') + d(o', o'') jest minimalną liczbą
ruchów potrzebnych do przekształcenia łańcucha opisywanego przez
o w łańcuch opisywany przez o'', przy czym w trakcie tego
przekształcenia, w pewnym momencie łańcuch jest opisywany przez
o'.
Wszystkie te własności sprawiają, że możemy traktować d jak
odległość między różnymi konfiguracjami łańcucha,
przy czym ostatnia z wymienionych własności odpowiada nierówności
trójkąta.
.
Jest tak dlatego, że d(o, o') + d(o', o'') jest minimalną liczbą
ruchów potrzebnych do przekształcenia łańcucha opisywanego przez
o w łańcuch opisywany przez o'', przy czym w trakcie tego
przekształcenia, w pewnym momencie łańcuch jest opisywany przez
o'.
Wszystkie te własności sprawiają, że możemy traktować d jak
odległość między różnymi konfiguracjami łańcucha,
przy czym ostatnia z wymienionych własności odpowiada nierówności
trójkąta.
Odległość d jest określona dla ciągów dowolnej długości.
Zdjęcie lub założenie k-tego ogniwa może wymagać wkładania lub
zdejmowania jedynie ogniw 1, 2, ..., k.
Położenie ogniw o numerach większych od k nie ma znaczenia dla
liczby ruchów potrzebnych do zdjęcia lub założenia k-tego
ogniwa.
Tak więc, dla dowolnych ciągów o, o' oraz r zachodzi
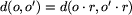 (
Symbol
(
Symbol  oznacza operację sklejania ciągów.
Dla uproszczenia, przez an będziemy oznaczać ciąg złożony z
n elementów a,
oznacza operację sklejania ciągów.
Dla uproszczenia, przez an będziemy oznaczać ciąg złożony z
n elementów a,
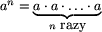 .
)
Zastanówmy się ile wynosi
.
)
Zastanówmy się ile wynosi 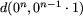 , czyli ile
ruchów należy wykonać, aby zdjąć n-te ogniwo, zakładając, że
ogniwa 1, 2, ..., n-1 są zdjęte i takie mają pozostać.
Otóż, żeby zdjąć n-te ogniwo, należy najpierw założyć ogniwo
n-1 i zdjąć ogniwa 1, 2, ..., n-2.
Następnie po zdjęciu n-tego ogniwa należy zdjąć również ogniwo
n-1.
Tak więc:
, czyli ile
ruchów należy wykonać, aby zdjąć n-te ogniwo, zakładając, że
ogniwa 1, 2, ..., n-1 są zdjęte i takie mają pozostać.
Otóż, żeby zdjąć n-te ogniwo, należy najpierw założyć ogniwo
n-1 i zdjąć ogniwa 1, 2, ..., n-2.
Następnie po zdjęciu n-tego ogniwa należy zdjąć również ogniwo
n-1.
Tak więc:
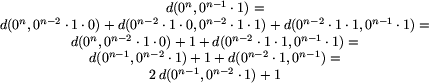
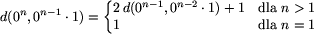
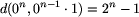
Oznaczmy przez R(o) = d(o, 0n) oraz
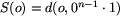 , gdzie n jest długością ciągu
o.
Naszym celem jest wyznaczenie wzoru na R(o).
Zauważmy, że zachodzą następujące zależności:
, gdzie n jest długością ciągu
o.
Naszym celem jest wyznaczenie wzoru na R(o).
Zauważmy, że zachodzą następujące zależności:
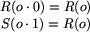
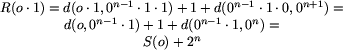
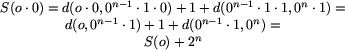
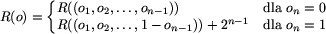
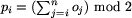 ,
czyli pi = 0, gdy wśród
,
czyli pi = 0, gdy wśród 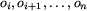 jest
parzysta liczba jedynek, w przeciwnym przypadku pi = 1.
Wówczas mamy:
jest
parzysta liczba jedynek, w przeciwnym przypadku pi = 1.
Wówczas mamy:
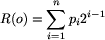
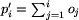 .
Zauważmy, że
.
Zauważmy, że 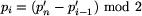 .
Możemy więc wyrazić R(o) następującym wzorem:
.
Możemy więc wyrazić R(o) następującym wzorem:
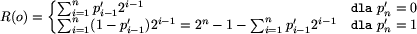
| 1 | { Inicjacja zmiennych. } |
| 2 | readln(we, n); |
| 3 | dodawac := false; |
| 4 | przypisz(wynik, 0); |
| 5 | przypisz(potega2, 1); |
| 6 | { Sumowanie kolejnych elementów szeregu 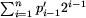 . } . } |
| 7 | for i := 1 to n do begin |
| 8 | if dodawac then |
| 9 | dodaj(wynik, potega2); |
| 10 | dodaj(potega2, potega2); |
| 11 | read(we, o); |
| 12 | if o = 1 then |
| 13 | dodawac := not dodawac |
| 14 | end; |
| 15 | { Obliczenie i zapisanie wyniku. } |
| 16 | if dodawac then begin |
| 17 | dodajjeden(wynik); |
| 18 | odejmij(potega2, wynik); |
| 19 | zapiszwynik(wy, potega2) |
| 20 | end end |
| 21 | zapiszwynik(wy, wynik); |
W naszym rozwiązaniu będziemy używać następujących zmiennych. Pliki wejściowy i wyjściowy to odpowiednio we i wy. Zmienna n to liczba ogniw, o reprezentuje kolejne ogniwa. Zmienna logiczna dodawac reprezentuje kolejne wartości p'. Obliczany szereg wyliczamy na zmiennej wynik, równocześnie na zmiennej potega2 obliczamy kolejne potęgi dwójki. Używamy też pomocniczej zmiennej całkowitej i. Oto rozwiązanie:
Zauważmy, że jeśli n jest długością danego ciągu, to liczba cyfr
w wyniku jest rzędu O(n), a liczba cyfr w największej obliczonej
potędze 2 jest rzędu 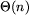 .
Tak więc złożoność pamięciowa programu jest rzędu
.
Tak więc złożoność pamięciowa programu jest rzędu 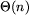 .
Program ten wykonuje
.
Program ten wykonuje 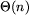 operacji, w tym operacje
arytmetyczne na dużych liczbach.
W rezultacie złożoność czasowa programu jest rzędu
operacji, w tym operacje
arytmetyczne na dużych liczbach.
W rezultacie złożoność czasowa programu jest rzędu 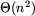 .
.
Pełne rozwiązanie można znaleźć na załączonej dyskietce w pliku lan.pas.