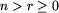 ,
,
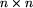 wypełniona
liczbami ze zbioru
wypełniona
liczbami ze zbioru 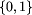 ;
kolumny i wiersze tabelki są ponumerowane od 1 do n;
liczbę znajdującą się w i-tej kolumnie i j-tym wierszu
tabelki oznaczamy przez F[i, j].
;
kolumny i wiersze tabelki są ponumerowane od 1 do n;
liczbę znajdującą się w i-tej kolumnie i j-tym wierszu
tabelki oznaczamy przez F[i, j].
| Tomasz Śmigielski | Marcin Mucha | Marcin Mucha |
| Treść zadania | Opracowanie | Program wzorcowy |
Dane są:
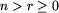 ,
,
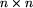 wypełniona
liczbami ze zbioru
wypełniona
liczbami ze zbioru 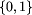 ;
kolumny i wiersze tabelki są ponumerowane od 1 do n;
liczbę znajdującą się w i-tej kolumnie i j-tym wierszu
tabelki oznaczamy przez F[i, j].
;
kolumny i wiersze tabelki są ponumerowane od 1 do n;
liczbę znajdującą się w i-tej kolumnie i j-tym wierszu
tabelki oznaczamy przez F[i, j].
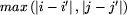 .
.
Należy obliczyć tabelkę W, 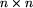 (do elementów tej tabelki
odwołujemy się tak samo, jak do elementów tabelki F)
taką, że W[i, j] jest sumą wszystkich liczb z tabelki F leżących
w odległości co najwyżej r od [i,j].
(do elementów tej tabelki
odwołujemy się tak samo, jak do elementów tabelki F)
taką, że W[i, j] jest sumą wszystkich liczb z tabelki F leżących
w odległości co najwyżej r od [i,j].
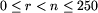 .
.
W kolejnych n wierszach znajduje się opis tabelki F.
Każdy z tych wierszy zawiera n liczb ze zbioru 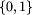 ,
pooddzielanych pojedynczymi odstępami, i-ta liczba zapisana w j+1-szym
wierszu to F[i,j].
,
pooddzielanych pojedynczymi odstępami, i-ta liczba zapisana w j+1-szym
wierszu to F[i,j].
5 1 1 0 0 0 1 1 1 1 0 0 1 0 0 0 0 0 0 0 1 1 0 1 0 0 0poprawną odpowiedzią jest plik wyjściowy map.out
3 4 2 2 1 4 5 2 2 1 3 4 3 3 2 2 2 2 2 2 1 1 2 2 2
W całym opracowaniu (które jest jednak nieco bardziej teoretyczne od programu)
będziemy zakładali,
że funkcja F jest określona na całym zbiorze 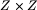 , przy czym poza rozważanym kwadratem się zeruje. To pozwoli na nieco swobodniejsze posługiwanie się sumami, a rozważenie przypadków brzegowych w programie jest dość proste (jeśli przypadki brzegowe będą w którymś momencie istotne, to zostanie to odnotowane).
, przy czym poza rozważanym kwadratem się zeruje. To pozwoli na nieco swobodniejsze posługiwanie się sumami, a rozważenie przypadków brzegowych w programie jest dość proste (jeśli przypadki brzegowe będą w którymś momencie istotne, to zostanie to odnotowane).
Rozwiązanie optymalne polega na dynamicznym policzeniu sum:
![S[i,j] = sum_(1 le x...](img/blue91.png)
Poszukiwane wartości wyrażają się przez S[i,j] następująco:
Zawsze można W[i,j] obliczyć przy pomocy czterech zagnieżdżonych pętli, czyli po prostu z definicji. Taki algorytm ma złożoność O(n2 r2) i nie należy do najszybszych. Jego implementacja znajduje się w pliku map1.pas.
Chwila zastanowienia wystarcza na znalezienie następującej sprytnej formuły:
![W[i,j]=W[i,j-1]+sum_...](img/blue92.png)
Oczywiście analogiczną formułę można zastosować, aby policzyć W[i,1] przy pomocy W[i-1,1]. Wtedy musielibyśmy ``faktycznie'' policzyć tylko W[1,1]. Wydaje się to jednak bezcelową komplikacją, skoro i tak program będzie miał złożoność O(n2 r). Nie jest to jednak takie proste. Poprawka bowiem nie zawsze wymaga czasu 2r. Czasami dodawana lub odejmowana kolumna jest poza zakresem i wtedy nic nie trzeba robić. Im większe r, tym częściej się to zdarza. W szczególności, jeśli r jest bardzo duże (np. r=n-1), to program ``poprawiający'' w pionie i w poziomie będzie działał w czasie O(n2), a ``poprawiający'' tylko w poziomie w czasie O(n3), z tego prostego powodu, że będzie musiał policzyć wszystkie W[i,1]. W związku z powyższym program ``poprawiający'' i w pionie i w poziomie można uznać za oddzielne rozwiązanie, a jego implementacja znajduje się w pliku map3.pas (choć pesymistycznie nie jest on szybszy od programu ``poprawiającego'' tylko w poziomie).
Wszystkie testy są losowe (nie bardzo widać, co mogłoby być lepsze). Różnią się rozmiarami, wartością r (z treści opracowania wynika, że generalnie najtrudniejsze testy to takie, dla których 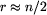 ) i czasem gęstością jedynek. Testy 1-4 to testy poprawnościowe. W szczególności test 1 sprawdza odporność na r=0, a test 3 na r bardzo duże. Dalej idą coraz trudniejsze testy wydajnościowe. Testy 11-13 to najtrudniejsze testy jakie udało się wymyśleć. Po drodze jest test 8, który może przejść nawet słaby algorytm, o ile przypadek małej liczby jedynek rozważa oddzielnie. Test 10 jest z kolei celowo dobrany pod algorytm poprawiający w obu kierunkach (tak naprawdę na testach 11-13 ten algorytm też radzi sobie nieco lepiej).
) i czasem gęstością jedynek. Testy 1-4 to testy poprawnościowe. W szczególności test 1 sprawdza odporność na r=0, a test 3 na r bardzo duże. Dalej idą coraz trudniejsze testy wydajnościowe. Testy 11-13 to najtrudniejsze testy jakie udało się wymyśleć. Po drodze jest test 8, który może przejść nawet słaby algorytm, o ile przypadek małej liczby jedynek rozważa oddzielnie. Test 10 jest z kolei celowo dobrany pod algorytm poprawiający w obu kierunkach (tak naprawdę na testach 11-13 ten algorytm też radzi sobie nieco lepiej).
Wydaje się, że świetnie napisany i zoptymalizowany algorytm, działający w czasie O(n2 r), przejdzie większość testów (być może nawet wszystkie). Oto charakterystyki poszczególnych testów: