| Krzysztof Loryś | Tomasz Waleń |
| Treść zadania, Opracowanie | Program wzorcowy |
Mrówki i biedronka
Jak wiadomo, mrówki potrafią ``hodować'' mszyce.
Mszyce wydzielają słodką rosę miodową, którą spijają mrówki.
Mrówki zaś bronią mszyc przed ich największymi wrogami - biedronkami.
Na drzewie obok mrowiska znajduje się
właśnie taka hodowla mszyc.
Mszyce żerują na liściach oraz w rozgałęzieniach drzewa.
W niektórych z tych miejsc znajdują się również mrówki patrolujące
drzewo.
Dla ustalenia uwagi, mrówki są ponumerowane od jeden w górę.
Hodowli zagraża biedronka, która zawsze siada na drzewie tam,
gdzie są mszyce, czyli
na liściach lub w rozgałęzieniach.
W chwili, gdy gdzieś na drzewie usiądzie biedronka, mrówki patrolujące
drzewo ruszają w jej stronę, aby ją przegonić.
Kierują się przy tym następującymi zasadami:
- z każdego miejsca na drzewie (liścia lub rozgałęzienia) można
dojść do każdego innego miejsca (bez zawracania) tylko na jeden
sposób; każda mrówka wybiera właśnie taką drogę do miejsca
lądowania biedronki,
- jeżeli w miejscu lądowania biedronki znajduje się mrówka,
biedronka natychmiast odlatuje,
- jeżeli na drodze, od aktualnego położenia mrówki do miejsca
lądowania biedronki, znajdzie się inna mrówka, to ta położona dalej
od biedronki kończy wędrówkę i zostaje w miejscu swojego
aktualnego położenia,
- jeżeli dwie lub więcej mrówek próbuje wejść na to samo rozgałęzienie
drzewa, to robi to tylko jedna mrówka - ta z najmniejszym numerem,
a reszta mrówek pozostaje na swoich miejscach
(liściach lub rozgałęzieniach),
- mrówka, która dociera do miejsca lądowania biedronki, przegania ją
i pozostaje w tym miejscu.
Biedronka jest uparta i znowu ląduje na drzewie.
Wówczas mrówki ponownie ruszają, aby przegonić intruza.
Dla uproszczenia przyjmujemy, że przejście gałązki łączącej
liść z rozgałęzieniem lub łączącej dwa rozgałęzienia, zajmuje
wszystkim mrówkom jednostkę czasu.
Zadanie
Napisz program, który:
- wczyta z pliku wejściowego mro.in opis drzewa,
początkowe położenia mrówek oraz miejsca, w których
kolejno siada biedronka,
- dla każdej mrówki znajdzie jej końcowe położenie
i wyznaczy liczbę mówiącą, ile razy przegoniła
ona biedronkę-0pt.
Wejście
W pierwszym wierszu pliku tekstowego mro.in znajduje się jedna
liczba całkowita n, równa łącznej liczbie liści i rozgałęzień w drzewie,
 .
Przyjmujemy, że liście i rozgałęzienia są ponumerowane od 1 do n.
W kolejnych n-1 wierszach są opisane gałązki - w każdym z tych
wierszy są zapisane dwie liczby całkowite a i b oznaczające,
że dana gałązka łączy miejsca a i b.
Gałązki pozwalają na przejście z każdego miejsca na drzewie, do
każdego innego miejsca.
W n+1-szym wierszu jest zapisana jedna liczba całkowita k,
.
Przyjmujemy, że liście i rozgałęzienia są ponumerowane od 1 do n.
W kolejnych n-1 wierszach są opisane gałązki - w każdym z tych
wierszy są zapisane dwie liczby całkowite a i b oznaczające,
że dana gałązka łączy miejsca a i b.
Gałązki pozwalają na przejście z każdego miejsca na drzewie, do
każdego innego miejsca.
W n+1-szym wierszu jest zapisana jedna liczba całkowita k,
 i
i 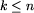 , równa liczbie mrówek patrolujących drzewo.
W każdym z kolejnych k wierszy zapisana jest jedna liczba całkowita
z przedziału od 1 do n.
Liczba zapisana w wierszu n+1+i oznacza początkowe położenie
mrówki nr i.
W każdym miejscu (liściu lub rozgałęzieniu) może znajdować się co
najwyżej jedna mrówka.
W wierszu n+k+2 zapisana jest jedna liczba całkowita l,
, równa liczbie mrówek patrolujących drzewo.
W każdym z kolejnych k wierszy zapisana jest jedna liczba całkowita
z przedziału od 1 do n.
Liczba zapisana w wierszu n+1+i oznacza początkowe położenie
mrówki nr i.
W każdym miejscu (liściu lub rozgałęzieniu) może znajdować się co
najwyżej jedna mrówka.
W wierszu n+k+2 zapisana jest jedna liczba całkowita l,
 ,
mówiąca ile razy biedronka siada na drzewie.
W każdym z kolejnych l wierszy zapisana jest jedna liczba całkowita
z zakresu od 1 do n.
Liczby te opisują kolejne miejsca, w których siada biedronka.
,
mówiąca ile razy biedronka siada na drzewie.
W każdym z kolejnych l wierszy zapisana jest jedna liczba całkowita
z zakresu od 1 do n.
Liczby te opisują kolejne miejsca, w których siada biedronka.
Wyjście
Twój program powinien zapisać k wierszy
w pliku wyjściowym mro.out. W i-tym wierszu powinny zostać
zapisane dwie liczby całkowite oddzielone pojedynczym odstępem -
końcowa pozycja i-tej mrówki (numer rozgałęzienia lub liścia) i
liczba mówiąca, ile razy przegoniła ona biedronkę.
Przykład
Dla pliku wejściowego mro.in:
4
1 2
1 3
2 4
2
1
2
2
2
4
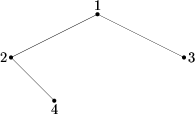
Rysunek 1. Drzewo dla przykładowych danych
poprawną odpwiedzią jest plik wyjściowy mro.out:
1 0
4 2
Rozwiązanie
Narzucający się schemat rozwiązania polega na symulacji kolejnych
zdarzeń (lądowań biedronki i pogoni mrówek). Po wylądowaniu
biedronki w wierzchołku drzewa (tj. liściu lub rozgałęzieniu)
symulujemy ruchy mrówek. Oznaczmy przez B wierzchołek, w którym
wylądowała biedronka. Kolejno dla każdej mrówki (wg rosnących
numerów) sprawdzamy czy droga między nią a wierzchołkiem B jest
wolna, tj. czy w żadnym wierzchołku na tej drodze nie znajduje się
jakaś inna mrówka. Jeśli droga jest wolna, przesuwamy mrówkę do
następnego wierzchołka.
Pierwszy problem z jakim musimy sobie poradzić, to sposób wyznaczania
drogi między wierzchołkami zajmowanymi przez mrówki a wierzchołkiem
B. W tym celu musimy przyjąć odpowiednią reprezentację drzewa w
pamięci. Wygodnie jest przyjąć, że dla każdego wierzchołka drzewa
pamiętamy listę jego sąsiadów oraz wskaźnik na ojca. Początkowo
jako korzeń możemy obrać dowolny wierzchołek drzewa a następnie, po
każdorazowym lądowaniu biedronki, modyfikować to drzewo tak, by
korzeniem zostawał wierzchołek B. Zauważmy, że modyfikacja ta
ograniczać się będzie do odwrócenia wskaźników pomiędzy
sąsiednimi wierzchołkami, leżącymi na ścieżce od
poprzedniego korzenia do wierzchołka B. Teraz dla każdej mrówki
droga do wierzchołka B wyznaczona jest poprzez wskaźniki na ojca.
Oczywistym jest, że złożoność czasowa tej fazy algorytmu jest
ograniczona przez O(n), gdzie n jest liczbą wierzchołków w
drzewie.
Drugi problem polega na efektywnym sprawdzaniu czy droga między
wierzchołkiem, w którym znajduje się mrówka a wierzchołkiem B
jest wolna. Jedno z rozwiązań polega na tym, by dla każdego
wierzchołka pamiętać znacznik, mówiący czy dany wierzchołek leży
na drodze wolnej. Początkowego ustawienia znaczników można dokonać
prostą procedurą przechodzenia drzewa, np. procedurą przechodzenia w
głąb. Każdy ruch mrówki może powodować konieczność
``zablokowania'' znaczników niektórych wierzchołków. Jeśli mrówka
przesunęła się do wierzchołka v, to należy zablokować znaczniki
wierzchołków leżących w poddrzewie o korzeniu v. Oczywiście
każdy znacznik będzie zablokowany co najwyżej jeden raz, a więc i ta
faza algorytmu ma złożoność czasową ograniczoną przez O(n).
W rozwiązaniu wzorcowym przyjęto inną metodę rozwiązania problemu
wolnych dróg. Wygląda ona na nieco bardziej skomplikowaną, jednak
pozwala na bardziej efektywną implementację algorytmu, zwłaszcza w
sytuacji gdy liczba mrówek m jest istotnie mniejsza od n.
Symulując ruchy mrówek zapamiętujemy w wierzchołkach ich ''ślady''
(numer mrówki i numer kroku). Każda mrówka przesuwana jest do przodu
dopóty, dopóki nie napotka wierzchołka z zapamiętanym śladem innej
mrówki, bądź też któraś z mrówek nie dojdzie do wierzchołka
B. Informacje zgromadzone w czasie symulacji pozwalają na wyliczenie
właściwych odległości, na jakie powinny się przemieścić
poszczególne mrówki. Zauważmy, że odległości te można by w prosty
sposób obliczyć przechodząc drzewo w głąb: dla każdej mrówki
jest to najmniejszy numer kroku zapamiętany w śladzie w wierzchołku
znajdującym się na drodze tej mrówki do B. Taka metoda nie byłaby
jednak specjalnie oszczędna. Jak łatwo zauważyć wszystkie istotne
dla tych obliczeń informacje znajdują się w śladach zapamiętanych
w tych wierzchołkach, w których doszło do ''spotkań'' mrówek ze
śladami innych mrówek. Można więc w trakcie symulacji zbudować graf
(a w istocie drzewo) spotkań i następnie zastosować do tego grafu
procedurę przechodzenia w głąb. Ponieważ graf ten ma O(m)
wierzchołków, taką też złożoność ma procedura przechodzenia tego
grafu.
Może się wydawać, że nie unikniemy jednak przechodzenia całego
drzewa (a więc kosztu zależnego od n) w drugiej fazie algorytmu,
ponieważ musimy pozacierać ślady przed symulacją kolejnego
lądowania biedronki. To fakt. Możemy jednak pamiętać ślady nie w
wierzchołkach drzewa, lecz w tablicy indeksowanej numerami
wierzchołków. Zacieranie śladów możemy wówczas wykonać, stosując
efektywne procedury zerowania tablicy.
Testy
Do testowania rozwiązania tego zadania użyto zestawu 15 testów:
- mro1.in - mały test poprawnościowy;
- mro1a.in - test poprawnościowy, mrówki we wszystkich węzłach;
- mro1b.in - test poprawnościowy, jedna mrówka;
- mro2.in - test poprawnościowy;
- mro2a.in - test poprawnościowy, drzewo z jednym węzłem;
- mro2b.in - test poprawnościowy;
- mro3.in - n=100, m=10, drzewo binarne;
- mro4.in - n=500, m=10, drzewo losowe;
- mro5.in - n=1000, m=10, drzewo binarne;
- mro6.in - n=3000, m=3, mrówki na gwieździe;
- mro7.in - n=5000, m=1000, mrówki na gwieździe;
- mro8.in - n=5000, drabinka, dwie biedronki;
- mro9.in - n=5000, dwie mrówki na liście z losowymi wypustkami, losowa biedronka;
- mro10.in - n=5000, dwie mrówki na liście;
- mro11.in - n=5000, m=3, mrówki na gwieździe.
 .
Przyjmujemy, że liście i rozgałęzienia są ponumerowane od 1 do n.
W kolejnych n-1 wierszach są opisane gałązki - w każdym z tych
wierszy są zapisane dwie liczby całkowite a i b oznaczające,
że dana gałązka łączy miejsca a i b.
Gałązki pozwalają na przejście z każdego miejsca na drzewie, do
każdego innego miejsca.
W n+1-szym wierszu jest zapisana jedna liczba całkowita k,
.
Przyjmujemy, że liście i rozgałęzienia są ponumerowane od 1 do n.
W kolejnych n-1 wierszach są opisane gałązki - w każdym z tych
wierszy są zapisane dwie liczby całkowite a i b oznaczające,
że dana gałązka łączy miejsca a i b.
Gałązki pozwalają na przejście z każdego miejsca na drzewie, do
każdego innego miejsca.
W n+1-szym wierszu jest zapisana jedna liczba całkowita k,
 i
i 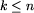 , równa liczbie mrówek patrolujących drzewo.
W każdym z kolejnych k wierszy zapisana jest jedna liczba całkowita
z przedziału od 1 do n.
Liczba zapisana w wierszu n+1+i oznacza początkowe położenie
mrówki nr i.
W każdym miejscu (liściu lub rozgałęzieniu) może znajdować się co
najwyżej jedna mrówka.
W wierszu n+k+2 zapisana jest jedna liczba całkowita l,
, równa liczbie mrówek patrolujących drzewo.
W każdym z kolejnych k wierszy zapisana jest jedna liczba całkowita
z przedziału od 1 do n.
Liczba zapisana w wierszu n+1+i oznacza początkowe położenie
mrówki nr i.
W każdym miejscu (liściu lub rozgałęzieniu) może znajdować się co
najwyżej jedna mrówka.
W wierszu n+k+2 zapisana jest jedna liczba całkowita l,
 ,
mówiąca ile razy biedronka siada na drzewie.
W każdym z kolejnych l wierszy zapisana jest jedna liczba całkowita
z zakresu od 1 do n.
Liczby te opisują kolejne miejsca, w których siada biedronka.
,
mówiąca ile razy biedronka siada na drzewie.
W każdym z kolejnych l wierszy zapisana jest jedna liczba całkowita
z zakresu od 1 do n.
Liczby te opisują kolejne miejsca, w których siada biedronka.
