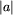 to długość słowa a;
to długość słowa a;
![u^((k)) = u[k+1..n]c...](img/blue320.png) (cykliczne przesunięcie słowa u o k pozycji w lewo);
(cykliczne przesunięcie słowa u o k pozycji w lewo);
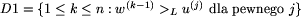 , gdzie >L oznacza porządek leksykograficzny na
słowach;
, gdzie >L oznacza porządek leksykograficzny na
słowach;
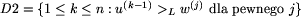 .
.
| A. Malinowski, W. Rytter | A. Malinowski | Paweł Wolff |
| Treść zadania | Opracowanie | Program wzorcowy |
W Bajtocji żyje bardzo znany jubiler Bajtazar. Zajmuje się on wyrobem naszyjników. Naszyjniki są zrobione z drogocennych kamieni nanizanych na nitkę. Do wyrobu naszyjników używa się 26-ciu rodzajów kamieni, będziemy je oznaczać małymi literami alfabetu (angielskiego): a, b, ..., z. Bajtazar postawił sobie za punkt honoru, aby nigdy nie wykonać dwóch takich samych naszyjników i przechowuje opisy wykonanych przez siebie naszyjników. Niektóre z tych naszyjników są bardzo długie. Dlatego też ich opisy mają skróconą postać. Każdy opis składa się z szeregu wielokrotnie powtórzonych sekwencji kamieni (wzorów). Opis naszyjnika to ciąg wzorów wraz z liczbami ich powtórzeń. Każdy wzór jest opisany za pomocą sekwencji liter reprezentujących kamienie tworzące wzór. Przykładowo, opis: abc 2 xyz 1 axc 3 reprezentuje naszyjnik abcabcxyzaxcaxcaxc powstały przez dwukrotne powtórzenie wzoru abc, jednokrotne wystąpienie wzoru xyz i trzykrotne powtórzenie wzoru axc. Sprawę dodatkowo utrudnia fakt, iż naszyjniki nie mają widocznego początku, ani końca i można je dowolnie obracać w kółko. Powyższy opis reprezentuje również np. naszyjniki cabcxyzaxcaxcaxcab oraz xcaxcaxcabcabcxyza.
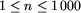 ), po której
występuje n opisów powtórzeń wzorów.
Opis powtórzeń i-tego wzoru składa się z:
liczby całkowitej li równej długości wzoru
(
), po której
występuje n opisów powtórzeń wzorów.
Opis powtórzeń i-tego wzoru składa się z:
liczby całkowitej li równej długości wzoru
(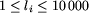 ),
słowa si złożonego z li małych liter alfabetu (angielskiego)
a, ..., z, reprezentującego wzór oraz
liczby całkowitej ki równej liczbie powtórzeń wzoru si
(
),
słowa si złożonego z li małych liter alfabetu (angielskiego)
a, ..., z, reprezentującego wzór oraz
liczby całkowitej ki równej liczbie powtórzeń wzoru si
(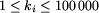 ).
Wiadomo, że suma liczb li (dla i = 1, ..., n) nie przekracza
10 000.
).
Wiadomo, że suma liczb li (dla i = 1, ..., n) nie przekracza
10 000.
3 3 abc 2 3 xyz 1 3 axc 3 4 4 cabc 1 4 xyza 1 3 xca 3 1 b 1poprawną odpowiedzią jest plik wyjściowy nas.out
TAK
Podczas zawodów dokonano następującej zmiany w treści zadania:
Naszyjniki powstałe jeden z drugiego przez odwrócenie kolejności kamieni nie muszą być identyczne, a więc np. opisy `abc' i `cba' nie reprezentują tego samego naszyjnika.
 (gdzie
(gdzie  oznacza konkatenację, czyli sklejenie słów).
Nasz problem można by zatem rozwiązać w czasie
proporcjonalnym do długości badanych słów, stosując
efektywny algorytm wyszukiwania wzorca w tekście. Znane są
dość wyrafinowane algorytmy wyszukiwania wzorca w czasie
liniowym bez użycia pomocniczych tablic (zob. np. [10]),
jednak cykliczną równoważność można sprawdzić znacznie prościej
(zob. [11]):
oznacza konkatenację, czyli sklejenie słów).
Nasz problem można by zatem rozwiązać w czasie
proporcjonalnym do długości badanych słów, stosując
efektywny algorytm wyszukiwania wzorca w tekście. Znane są
dość wyrafinowane algorytmy wyszukiwania wzorca w czasie
liniowym bez użycia pomocniczych tablic (zob. np. [10]),
jednak cykliczną równoważność można sprawdzić znacznie prościej
(zob. [11]):
Wprowadźmy oznaczenia:
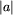 to długość słowa a;
to długość słowa a;
![u^((k)) = u[k+1..n]c...](img/blue320.png) (cykliczne przesunięcie słowa u o k pozycji w lewo);
(cykliczne przesunięcie słowa u o k pozycji w lewo);
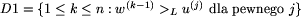 , gdzie >L oznacza porządek leksykograficzny na
słowach;
, gdzie >L oznacza porządek leksykograficzny na
słowach;
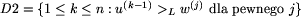 .
.
| 1 | { Algorytm sprawdzania, czy u powstaje przez cykliczne przesunięcie w } |
| 2 | { Niech 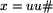 , y = , y = 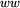 , n= , n= u u } } |
| 3 | begin |
| 4 | i := 0; j := 0; k := 1; |
| 5 | while (i < n) and (j < n) and (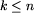 ) do ) do |
| 6 | begin |
| 7 | k := 1; |
| 8 | while x[i+k] = y[j+k] do |
| 9 | k := k+1; |
| 10 | if 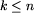 then then |
| 11 | if x[i+k] > y[j+k] then |
| 12 | i := i+k |
| 13 | end |
| 14 | j := j+k |
| 15 | { Niezmiennik: ![[1..i]subseteq D1](img/blue327.png) , , ![[1..j]subseteq D2](img/blue328.png) } } |
| 16 | end |
| 17 | end; |
| 18 | { u jest cyklicznym przesunięciem w wtedy i tylko wtedy, gdy k > n } |
Algorytm działa w czasie liniowym względem n, a jego poprawność wynika z podanego niezmiennika oraz z faktu, że jeśli D1 = [1..n] lub D2 = [1..n], to słowa u i w nie są cyklicznie równoważne.
Dodatkową trudność w zadaniu stanowi to, że opisy
naszyjników są podane w formie skompresowanej. Żeby uzyskać
program działający w czasie proporcjonalnym nie do
faktycznego rozmiaru samych naszyjników, ale raczej do
rozmiaru ich opisów, musimy odpowiednio zaimplementować
pętlę w wierszach 8-9. W naszym przypadku wystarczy, żebyśmy potrafili
efektywnie rozstrzygać, czy któreś ze słów al, br (gdzie
al oznacza konkatenację l kopii słowa a) jest
prefiksem (czyli fragmentem początkowym) drugiego słowa.
Nietrudno pokazać, że jeśli 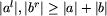 , to powyższy
warunek jest równoważny temu, że
, to powyższy
warunek jest równoważny temu, że 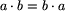 . Stąd
wynika, że w celu stwierdzenia, czy któreś ze słów al,
br jest prefiksem drugiego, wystarczy porównać tylko
. Stąd
wynika, że w celu stwierdzenia, czy któreś ze słów al,
br jest prefiksem drugiego, wystarczy porównać tylko
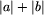 początkowych liter tych słów.
początkowych liter tych słów.
Usprawnienia wymagają jeszcze wiersze 12 i 14 w algorytmie. Z podanego niezmiennika wynika, że jeśli na pozycji i+k (odpowiednio j+k) mamy do czynienia z co najmniej drugim powtórzeniem pewnego wzoru, to bez zaburzenia niezmiennika możemy od razu przeskoczyć do ostatniego powtórzenia tego wzoru.