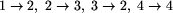 oraz
oraz
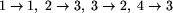 są takie same -
wystarczy ułożyć żetony na stole w rzędzie,
w pierwszym przypadku w kolejności od lewej do prawej,
a w drugim od prawej do lewej, a pchły odtańczą ten sam taniec.
są takie same -
wystarczy ułożyć żetony na stole w rzędzie,
w pierwszym przypadku w kolejności od lewej do prawej,
a w drugim od prawej do lewej, a pchły odtańczą ten sam taniec.
| Marcin Sawicki | Andrzej Gąsienica--Samek |
| Treść zadania, Opracowanie | Program wzorcowy |
W Bajtocji można spotkać wędrownych treserów pcheł. Tresowane pchły uczone są tańca, polegającego na wykonywaniu precyzyjnych skoków w rytm muzyki. Dokładnie wygląda to tak: treser układa na stole w rządku ponumerowane żetony, przy czym żetony nie muszą być ułożone po kolei. Na każdym żetonie, oprócz jego numeru, jest również napisany numer żetonu, na który powinna z niego skoczyć pchła. Następnie treser ustawia po jednej pchle na każdym z żetonów i włącza muzykę. Na początku każdego taktu, każda z pcheł wykonuje skok wprost na żeton, którego numer jest napisany na żetonie, na którym w danej chwili stoi. W trakcie tańca może się zdarzyć, że kilka pcheł znajdzie się na tym samym żetonie i razem wykonują dalsze skoki.
Załóżmy, że mamy n tresowanych pcheł i n żetonów. Jeśli podamy, jakie liczby znajdują się kolejno na żetonach numer 1, 2, ..., n, to jednoznacznie opiszemy układ choreograficzny, jaki zaprezentują pchły. Jednak może się okazać, że dwa różne zestawy żetonów dają ten sam układ, jeśli tylko odpowiednio je ułożymy.
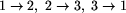 ),
to pchły będą tańczyć ,,w kółko''
i żadne dwie nigdy się nie spotkają na tym samym żetonie.
Jest to inny układ tańca, niż np.
),
to pchły będą tańczyć ,,w kółko''
i żadne dwie nigdy się nie spotkają na tym samym żetonie.
Jest to inny układ tańca, niż np.
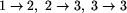 ,
gdzie już po dwóch taktach wszystkie trzy pchły spotkają się
na żetonie nr 3 i dalej będą razem skakać w miejscu.
,
gdzie już po dwóch taktach wszystkie trzy pchły spotkają się
na żetonie nr 3 i dalej będą razem skakać w miejscu.
Natomiast układy
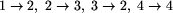 oraz
oraz
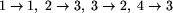 są takie same -
wystarczy ułożyć żetony na stole w rzędzie,
w pierwszym przypadku w kolejności od lewej do prawej,
a w drugim od prawej do lewej, a pchły odtańczą ten sam taniec.
są takie same -
wystarczy ułożyć żetony na stole w rzędzie,
w pierwszym przypadku w kolejności od lewej do prawej,
a w drugim od prawej do lewej, a pchły odtańczą ten sam taniec.
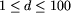 .
.
Kolejne 3d wierszy pliku pch.in opisują kolejne przypadki
testowe -
każdy przypadek zajmuje trzy kolejne wiersze pliku.
Pierwszy z nich zawiera jedną liczbę całkowitą 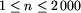 ,
równą liczbie żetonów.
Każdy z dwóch następnych wierszy zawiera opis zestawu n żetonów
w postaci ciągu n liczb całkowitych z przedziału 1... n,
pooddzielanych pojedynczymi odstępami;
i-ty wyraz ciągu oznacza numer żetonu, na który mają skakać pchły
z żetonu nr i.
,
równą liczbie żetonów.
Każdy z dwóch następnych wierszy zawiera opis zestawu n żetonów
w postaci ciągu n liczb całkowitych z przedziału 1... n,
pooddzielanych pojedynczymi odstępami;
i-ty wyraz ciągu oznacza numer żetonu, na który mają skakać pchły
z żetonu nr i.
2 3 2 3 1 2 3 3 4 2 3 2 4 1 3 2 3poprawną odpowiedzią jest plik wyjściowy pch.out
N T
Wypada nam zacząć od przypomnienia, co to jest graf.
Graf są to kropki, z których niektóre połączone są strzałkami.
Albo inaczej: graf G jest to para uporządkowana 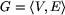 , gdzie
V jest dowolnym zbiorem, który nazwiemy zbiorem wierzchołków grafu, zaś
, gdzie
V jest dowolnym zbiorem, który nazwiemy zbiorem wierzchołków grafu, zaś
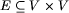 jest zbiorem krawędzi: jeżeli
jest zbiorem krawędzi: jeżeli 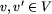 są dwoma
wierzchołkami grafu, to są one połączone strzałką od v do v' wtedy i
tylko wtedy, gdy para
są dwoma
wierzchołkami grafu, to są one połączone strzałką od v do v' wtedy i
tylko wtedy, gdy para 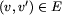 .
.
Zwróćmy uwagę, że w przyjętej przez nas definicji krawędź od v do v' to nie to samo, co krawędź od v' do v. Ponadto, dopuszczamy pętle, czyli krawędzie prowadzące od wierzchołka do niego samego.
Grafy są przydatne do opisu wielu praktycznych zagadnień, np. sieci komunikacyjnych, obwodów elektrycznych, zależności pomiędzy etapami przedsięwzięcia, a także, jak się zaraz okaże, pchlej choreografii.
Kiedy rysujemy graf, zazwyczaj nie ma dla nas znaczenia, jak na naszym
rysunku rozmieszczone są wierzchołki, ważne jest tylko, które z którymi są
połączone. Poza tym często wszystkie wierzchołki grafu zaznaczamy tak samo
(np. kropką). Stąd pojawia się problem izomorfizmu grafów,
polegający na rozstrzygnięciu, czy dane dwa grafy 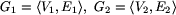 da się
narysować tak samo? Innymi słowy, chodzi o sparowanie wierzchołków grafu G1
z wierzchołkami grafu G2 tak, by krawędzie w grafie G1 dokładnie
odpowiadały krawędziom pomiędzy wierzchołkami do pary w grafie G2.
Jeszcze inaczej, chodzi o znalezienie funkcji wzajemnie jednoznacznej
da się
narysować tak samo? Innymi słowy, chodzi o sparowanie wierzchołków grafu G1
z wierzchołkami grafu G2 tak, by krawędzie w grafie G1 dokładnie
odpowiadały krawędziom pomiędzy wierzchołkami do pary w grafie G2.
Jeszcze inaczej, chodzi o znalezienie funkcji wzajemnie jednoznacznej
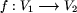 takiej, by
takiej, by 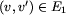 zachodziło wtedy i tylko
wtedy, gdy
zachodziło wtedy i tylko
wtedy, gdy 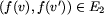 .
.
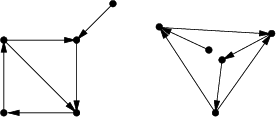
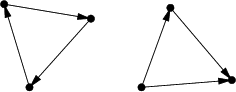
Wróćmy teraz do naszego zadania. Mamy opis pewnego tańca pcheł, czyli n
żetonów ponumerowanych liczbami 1,2,...,n, a na każdym z nich
dodatkową liczbę mówiącą, na który żeton pchła ma skoczyć. Rozważmy graf,
którego zbiorem wierzchołków będzie właśnie 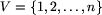 ,
czyli każdemu żetonowi odpowiada dokładnie jeden wierzchołek grafu.
Krawędzie poprowadzimy oczywiście od każdego żetonu do tego, którego numer
jest na nim zapisany. Krawędzie będą zatem odpowiadać pchlim skokom.
,
czyli każdemu żetonowi odpowiada dokładnie jeden wierzchołek grafu.
Krawędzie poprowadzimy oczywiście od każdego żetonu do tego, którego numer
jest na nim zapisany. Krawędzie będą zatem odpowiadać pchlim skokom.
Teraz naprawdę nietrudno zauważyć, że nasze zadanie to po prostu pytanie o izomorfizm tak utworzonych grafów! Zaglądamy zatem do indeksu dowolnego podręcznika algorytmiki, znajdujemy hasło ,,grafów izomorfizm'' i ... co za rozczarowanie! Okazuje się, że nie jest znany żaden wielomianowy algorytm na rozstrzyganie o izomorfizmie grafów. Nikt też nie zdołał udowodnić, że taki algorytm nie może istnieć, co więcej nie wiadomo nawet, czy jest to tzw.problem NP-zupełny.(Problemy NP-zupełne to m.in. problem cyklu Hamiltona, problem komiwojażera, problem 3-kolorowania grafu, sumy podzbioru, maksymalnej kliki, spełnialności formuł boolowskich i kilkaset innych. Wiadomo o tych problemach tyle, że albo wszystkie mają rozwiązania wielomianowe, albo żaden z nich takiego rozwiązania nie ma. Ponieważ przez wiele lat nie wymyślono dla żadnego z nich algorytmu wielomianowego (za to wymyślono wiele naprawdę pomysłowych algorytmów dla innych problemów), więc większość informatyków przypuszcza, że takie algorytmy nie istnieją. Wciąż jednak nikt nie potrafi tego udowodnić. Więcej o problemach NP i NP-zupełnych można poczytać w znakomitej książce [14].)
Czyżby było aż tak źle? Pomyślmy... niektórzy spośród czytelników słyszeli może o problemie izomorfizmu drzew, dla którego istnieje rozwiązanie wielomianowe. Drzewa to grafy bez cykli. Być może grafy, które opisują pchle harce, też mają jakąś szczególną postać, która pozwala łatwo rozwiązać nasz problem? Okazuje się, że tak.
Przede wszystkim, w naszych grafach z każdego wierzchołka wychodzi dokładnie jedna krawędź. Oczywiście jest całe mnóstwo grafów, które nie mają tej właściwości, np. trzy spośród czterech narysowanych powyżej.
Zdefiniujmy cykl (skierowany) jako ciąg (v1,v2,...,vn)
parami różnych wierzchołków grafu
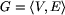 taki, że dla każdego i=1,2,...,n-1 mamy w grafie
krawędź
taki, że dla każdego i=1,2,...,n-1 mamy w grafie
krawędź 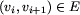 oraz dodatkowo
oraz dodatkowo 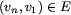 .
Zauważmy, że jeżeli ciąg (v1,v2,...,vn) jest cyklem, to
dla każdego i=2,3,..., n
cyklem jest
także ciąg
.
Zauważmy, że jeżeli ciąg (v1,v2,...,vn) jest cyklem, to
dla każdego i=2,3,..., n
cyklem jest
także ciąg 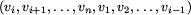 , otrzymany
przez cykliczne przesunięcie ciągu wyjściowego w lewo o i-1 pozycji.
Umówmy się, że są to równoważne reprezentacje jednego i tego samego cyklu.
, otrzymany
przez cykliczne przesunięcie ciągu wyjściowego w lewo o i-1 pozycji.
Umówmy się, że są to równoważne reprezentacje jednego i tego samego cyklu.
A co możemy powiedzieć o cyklach w naszych pchlich grafach?
Wykażemy, że są one rozłączne, to znaczy
że każdy wierzchołek należy do co najwyżej jednego cyklu.
Dlaczego? Przypuśćmy, że wierzchołek v=vi=v'j należy do dwóch cykli:
v1,v2,...,vn oraz v'1,v'2,...,v'm.
Umówiliśmy się, że ciągi reprezentujące cykle możemy przesuwać cyklicznie,
zatem nic nie stracimy zakładając, że v=v1=v'1 (czyli że i=j=1).
Zamieniając w razie potrzeby cykle rolami możemy również przyjąć, że 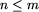 .
Wiemy, że z wierzchołka v
(podobnie jak z każdego innego)
wychodzi dokładnie jedna krawędź, wiemy też, że
mamy w naszym grafie krawędź (v1,v2) oraz (v'1,v'2). Skoro
zatem v=v1=v'1, to także v2=v'2. Rozumując tak dalej wnioskujemy,
że v3=v'3,..., vn=v'n. Jeżeli byłoby m>n, to mielibyśmy
następnie
.
Wiemy, że z wierzchołka v
(podobnie jak z każdego innego)
wychodzi dokładnie jedna krawędź, wiemy też, że
mamy w naszym grafie krawędź (v1,v2) oraz (v'1,v'2). Skoro
zatem v=v1=v'1, to także v2=v'2. Rozumując tak dalej wnioskujemy,
że v3=v'3,..., vn=v'n. Jeżeli byłoby m>n, to mielibyśmy
następnie 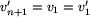 , lecz jest to niemożliwe, bo umówiliśmy się,
że żaden wierzchołek w cyklu się nie powtarza. Czyli n=m i nasze cykle
okazały się być jednym i tym samym cyklem (a nawet tą samą jego
reprezentacją)!
, lecz jest to niemożliwe, bo umówiliśmy się,
że żaden wierzchołek w cyklu się nie powtarza. Czyli n=m i nasze cykle
okazały się być jednym i tym samym cyklem (a nawet tą samą jego
reprezentacją)!
Każdy wierzchołek w naszym grafie albo należy do jakiegoś jednego cyklu,
albo nie należy do żadnego. Jak wygląda ten drugi przypadek? Niech
wierzchołek v1 nie należy do żadnego cyklu. Prowadzi z niego dokładnie
jedna krawędź, umówmy się, że do wierzchołka v2, z którego z kolei
prowadzi krawędź do v3 itd. Otrzymujemy ciąg wierzchołków
v1,v2,v3,v4,....
Wiemy, że v1 występuje tylko na początku ciągu (skoro nie leży na żadnym
cyklu). Jednak w naszym grafie jest tylko skończenie wiele wierzchołków,
więc od któregoś miejsca muszą się one zacząć powtarzać. Niech n będzie
najmniejszą taką liczbą, że istnieje i<n takie, że vi=vn. Oczywiście
i>1. Chwila uwagi wystarcza by stwierdzić, że wierzchołki
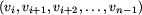 tworzą cykl. Być może n=i+1, mamy
wówczas cykl jednoelementowy, czyli pętlę przy wierzchołku vi.
tworzą cykl. Być może n=i+1, mamy
wówczas cykl jednoelementowy, czyli pętlę przy wierzchołku vi.
Podsumujmy: startując od dowolnego wierzchołka i podążając po strzałkach, albo jesteśmy od razu na cyklu, albo po jakimś czasie wpadamy na cykl. Sytuacja przypomina morza i rzeki: jeżeli jesteśmy w wodzie, to albo jesteśmy w morzu, i wtedy wiadomo w jakim, albo jesteśmy w rzece i w końcu spłyniemy do morza. Do tego wiadomo, w zlewisku jakiego morza leży dana rzeka. Co więcej, analogia obejmuje i to, że rzeka ma dopływy. Istotnie, ścieżki prowadzące od różnych wierzchołków do tego samego cyklu mogą się łączyć jeszcze przed osiągnięciem cyklu, tworząc podczepione do cykli drzewa. Przykładowo, wygląda to tak, jak na rysunku []. Wierzchołki, które leżą na cyklach, zaznaczono na szaro.
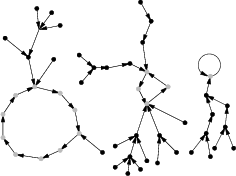
Wcześniej wspominaliśmy o problemie izomorfizmu drzew, dla którego znamy
rozwiązanie w czasie wielomianowym. Rozwiązanie to polega na wyznaczeniu
dla drzewa D jego sygnatury 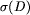 , to znaczy takiego drzewa, że
jeżeli D i D' są izomorficzne, to
, to znaczy takiego drzewa, że
jeżeli D i D' są izomorficzne, to 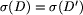 . Następnie po
prostu porównujemy otrzymane sygnatury. Jak można zdefiniować taką
sygnaturę?
. Następnie po
prostu porównujemy otrzymane sygnatury. Jak można zdefiniować taką
sygnaturę?
Rozważmy najpierw prosty przykład porównywania ciągów liczb. Chcielibyśmy wiedzieć, czy dwa ciągi reprezentują ten sam zbiór wartości. Jedno z możliwych rozwiązań polega na posortowaniu ich i stwierdzeniu, czy są identyczne. Sortowanie to w tym wypadku właśnie wyznaczenie sygnatury.
Izomorfizm drzew (z wyróżnionym korzeniem) polega wyłącznie na permutowaniu synów każdego węzła. Sygnaturę wyznaczymy zatem, biorąc jakąś wyróżnioną permutację. Jaką? Np. najmniejszą, o ile nauczymy się porównywać drzewa. Przyjmijmy taką definicję:
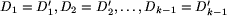 i przy tym Dk<D'k
dla pewnego
i przy tym Dk<D'k
dla pewnego 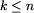 , to
także D<D' (tzn. aby porównać drzewa D i D', potrzebujemy porównać
leksykograficznie ciągi synów ich korzeni).
, to
także D<D' (tzn. aby porównać drzewa D i D', potrzebujemy porównać
leksykograficznie ciągi synów ich korzeni).
Za sygnaturę drzewa obieramy teraz po prostu najmniejsze możliwe w sensie określonego wyżej porządku drzewo, izomorficzne z danym. Wyznaczamy ją w ten sposób, że idąc od liści do korzenia, w każdym wierzchołku sortujemy synów w kolejności od tego, pod którym jest zaczepione najmniejsze poddrzewo (w zdefiniowanym wyżej sensie) do tego, pod którym zaczepione jest największe.
Sądzę, że nie jest już teraz trudno zdefiniować sygnatury dla zadania o pchłach. Nasze grafy rozpadają się na rozłączne cykle, z których do każdego podczepione są drzewa. Pierwszym krokiem jest zastąpienie każdego drzewa jego sygnaturą. Następnie można znaleźć dla każdego cyklu taką jego reprezentację (rotację) (v1,...,vn), by po zastąpieniu każdego wierzchołka w tym ciągu sygnaturą podczepionego do niego drzewa (być może zbudowanego tylko z korzenia), otrzymać leksykograficznie najmniejszy możliwy ciąg drzew. Z kolei można porównywać tak otrzymane sygnatury różnych cykli z podoczepianymi drzewami. W rozwiązaniu wzorcowym są one porównywane leksykograficznie. Inną możliwością byłoby najpierw porównywanie długości cykli, a następnie porównywanie leksykograficzne podczepionych drzew tylko dla cykli równej długości (analogicznie do definicji porządku na drzewach, podanej powyżej). Sygnaturą dla całego grafu jest uporządkowany ciąg wszystkich występujących w nim cykli. Sprawdzenie, że identyczne sygnatury otrzymujemy wtedy i tylko wtedy, gdy grafy są izomorficzne, nie powinno być problemem, jeśli ktoś potrafi udowodnić to dla drzew.
Jeżeli komuś powyższy opis nie wystarczył, to po szczegóły odsyłam do kodu programu wzorcowego.
Wydzielenie w grafie cykli oraz wierzchołków nie leżących na cyklach i zbudowanie struktury ojców/synów w drzewach jest proste i może być wykonane w czasie liniowym.
Następnie dla każdego drzewa musimy obliczyć sygnaturę. Oznacza to konieczność posortowania synów każdego węzła. Sortowanie wymaga wykonania pewnej liczby porównań, a każde porównanie w pesymistycznym przypadku kosztuje tyle, co minimum z rozmiaru porównywanych poddrzew. W rozwiązaniu firmowym dla uproszczenia zastosowano sortowanie przez wstawianie. W sortowaniu tym każda para elementów jest porównywana co najwyżej raz. Pozwala to oszacować koszt wyznaczenia sygnatury całego drzewa poprzez następującą obserwację: każdy węzeł drzewa co najwyżej raz bierze udział w porównaniu z poddrzewem, zawieszonym w każdym innym węźle, leżącym na takiej jak on lub mniejszej głębokości (odległości od korzenia). Jeżeli drzewo ma n wierzchołków, pozwala to oszacować koszt obliczenia sygnatury tego drzewa przez O(n2) (gdyż w sumie we wszystkich operacjach porównania poddrzew każdy z wierzchołków będzie brał udział co najwyżej n razy). Oczywiście, jeżeli mamy las drzew, które w sumie mają n wierzchołków, to tym bardziej łączny koszt wyznaczenia sygnatury dla każdego z nich jest O(n2).
Z kolei trzeba wyznaczyć sygnatury dla poszczególnych cykli. Dla cyklu długości k wymaga to k porównań cykli (a dokładniej, różnych rotacji tego samego cyklu), by znaleźć minimalną rotację. Każde porównanie angażuje każdy z wierzchołków grafu co najwyżej raz, więc w sumie znalezienie minimalnej rotacji dla każdego z cykli wymaga O(n2) operacji.
Na koniec podobna argumentacja co przy wyznaczaniu sygnatur pozwala stwierdzić, że posortowanie przez wstawianie wszystkich cykli w grafie o n wierzchołkach również wymaga O(n2) operacji. Podsumowując, całe zadanie rozwiążemy w czasie O(n2).
Dla szczególnie dociekliwego Czytelnika mamy zadanie: czy można ten problem rozwiązać w czasie mniejszym od kwadratowego? Dla których etapów obliczenia (wyznaczanie sygnatur drzew, cykli, całego grafu) potrafiłbyś znaleźć szybszy algorytm?
Ponieważ zadanie wymaga podania jedynie odpowiedzi ,,tak'' lub ,,nie'', więc każdy z 10 właściwych testów obejmował od 20 do 100 przypadków, aby wyeliminować programy, próbujące zgadywać odpowiedź na chybił-trafił.
Testy zostały wygenerowane losowo, przy użyciu następujących parametrów:
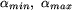 - ograniczenia na to, jaki
ułamek liczby żetonów
w każdej ze składowych grafu znajduje się na cyklu
- ograniczenia na to, jaki
ułamek liczby żetonów
w każdej ze składowych grafu znajduje się na cyklu
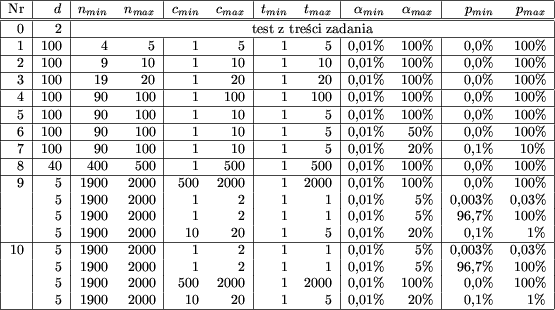
Testy 1-3 były prostymi testami poprawnościowymi. Niewykluczone, że mogły być rozwiązane nawet przez algorytm wykładniczy, który np. szukałby izomorfizmu, badając wszystkie możliwe permutacje zbioru wierzchołków grafu. Na testach 4-7 pewne szanse miały rozwiązania, działające w czasie sześciennym. Przez ostatnie trzy testy przechodziły tylko algorytmy o złożoności czasowej O(n2).