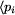 ,
, 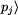 ,
(dla
,
(dla 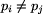 )
oznaczają możliwe, bezpośrednie przejazdy od przystanku pi do
pj (
)
oznaczają możliwe, bezpośrednie przejazdy od przystanku pi do
pj (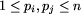 ).
).
| Zbigniew J. Czech | Marcin Stefaniak |
| Treść zadania, Opracowanie | Program wzorcowy |
Rozważmy graf opisujący sieć komunikacji publicznej,
np. sieć autobusową, tramwajową, metra, itp.
Wierzchołki grafu, o numerach 1, 2, ..., n, reprezentują
przystanki, a krawędzie 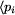 ,
, 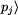 ,
(dla
,
(dla 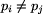 )
oznaczają możliwe, bezpośrednie przejazdy od przystanku pi do
pj (
)
oznaczają możliwe, bezpośrednie przejazdy od przystanku pi do
pj (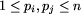 ).
).
W sieci kursują pojazdy linii komunikacyjnych.
Linie komunikacyjne oznaczone są numerami 1, 2, ..., k.
Linia komunikacyjna l zdefiniowana jest przez ciąg przystanków
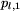 ,
, 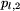 , ...,
, ..., 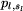 ,
przez które przejeżdżają pojazdy linii, oraz czasy
przejazdów
,
przez które przejeżdżają pojazdy linii, oraz czasy
przejazdów 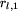 ,
, 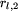 , ...,
, ..., 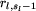 pomiędzy przystankami -
pomiędzy przystankami - 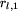 jest czasem przejazdu od przystanku
jest czasem przejazdu od przystanku
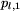 do
do 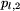 , lub z powrotem, tj. od przystanku
, lub z powrotem, tj. od przystanku
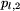 do
do 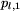 ;
;
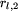 jest czasem przejazdu od przystanku
jest czasem przejazdu od przystanku 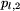 do
do 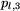 , itd.
Wszystkie przystanki linii są różne, tj. dla
, itd.
Wszystkie przystanki linii są różne, tj. dla 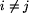 zachodzi
zachodzi
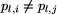 .
.
Na danej linii l pojazdy kursują z określoną częstotliwością
cl, gdzie cl jest liczbą ze zbioru 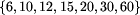 .
Pojazdy linii wyruszają z przystanku
.
Pojazdy linii wyruszają z przystanku 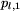 o każdej ``okrągłej''
godzinie doby, g:0, (
o każdej ``okrągłej''
godzinie doby, g:0, (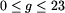 ),
a następnie zgodnie z częstotliwością linii, a więc o godzinach
g:cl, g:2cl, ... itd.
(g:cl oznacza "`cl minut po godzinie g'').
Ruch pojazdów linii odbywa się jednocześnie w obu kierunkach:
z przystanku
),
a następnie zgodnie z częstotliwością linii, a więc o godzinach
g:cl, g:2cl, ... itd.
(g:cl oznacza "`cl minut po godzinie g'').
Ruch pojazdów linii odbywa się jednocześnie w obu kierunkach:
z przystanku 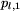 do
do 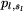 ,
a także z przystanku
,
a także z przystanku 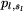 do
do 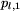 .
Godziny odjazdów pojazdów linii z przystanku
.
Godziny odjazdów pojazdów linii z przystanku 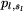 są takie same,
jak z przystanku
są takie same,
jak z przystanku 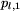 .
.
W tak zdefiniowanej sieci komunikacji publicznej chcemy odbyć podróż z przystanku początkowego x, do przystanku końcowego y. Zakładamy, że podróż jest możliwa i nie będzie trwała dłużej niż 24 godziny. W trakcie podróży możemy się przesiadać dowolną liczbę razy z jednej linii komunikacyjnej na inną. Przyjmujemy, że czas dokonania przesiadki jest równy 0, jednakowoż, zmieniając linię musimy liczyć się z koniecznością czekania na pojazd linii, do którego chcemy się przesiąść. Naszym celem jest odbycie podróży z przystanku początkowego x, do przystanku końcowego y, w jak najkrótszym czasie.
| 1 |
| 2 |
| 1 |
| 2 |
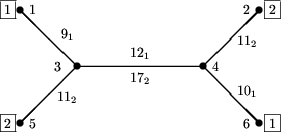
Załóżmy, że o godzinie 23:30 znajdujemy się na przystanku początkowym 5 i chcemy odbyć podróż do przystanku końcowego 6. Wówczas musimy odczekać 10 minut i o godzinie 23:40 wyjeżdżamy linią
| 2 |
| 1 |
| 2 |
| 1 |
 ),
),
 ),
),
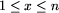 ),
),
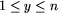 ),
),
 ),
),
 ).
).
W kolejnych 3k wierszach opisane są kolejne linie komunikacyjne - opis każdej linii zajmuje trzy kolejne wiersze.
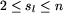 ), oraz
cl, równa częstotliwości kursowania pojazdów
(
), oraz
cl, równa częstotliwości kursowania pojazdów
(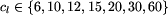 ).
).
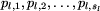 - numery kolejnych przystanków na tej linii
(
- numery kolejnych przystanków na tej linii
(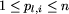 , dla
, dla 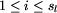 ).
).
 - czasy przejazdów (w minutach) pomiędzy kolejnymi
przystankami na tej linii
(
- czasy przejazdów (w minutach) pomiędzy kolejnymi
przystankami na tej linii
(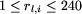 ,
dla
,
dla 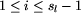 ).
).
Suma liczb przystanków, na wszystkich liniach razem, nie przekracza 4000
(tzn. 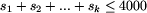 ).
).
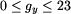 ) oraz minutę dotarcia do przystanku końcowego
my (
) oraz minutę dotarcia do przystanku końcowego
my (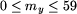 ).
).
6 2 5 6 23 30 4 15 1 3 4 6 9 12 10 4 20 5 3 4 2 11 17 11poprawną odpowiedzią jest plik wyjściowy pod.out
0 16
W pierwszej kolejności zaprojektujemy strukturę danych, w której
będziemy przechowywać
rozkład jazdy pojazdów. Z zadania wynika, że
sieć komunikacyjna działa całą dobę. Pojazdy linii komunikacyjnych
wyruszają z przystanków
krańcowych z określoną częstotliwością, c, gdzie
c jest liczbą ze zbioru 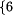 ,
10, 12, 15, 20, 30,
,
10, 12, 15, 20, 30, 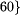 . Ponieważ każda z tych
częstotliwości dzieli liczbę 60, to pojazdy danej linii będą odjeżdżać
z przystanków zawsze w tych samych minutach dowolnej godziny. Przykładowo,
niech dla pewnej linii c=15. Wówczas pojazdy tej linii wyruszają z przystanku
p1
o godzinie g minut 0, 15, 30, 45, gdzie
. Ponieważ każda z tych
częstotliwości dzieli liczbę 60, to pojazdy danej linii będą odjeżdżać
z przystanków zawsze w tych samych minutach dowolnej godziny. Przykładowo,
niech dla pewnej linii c=15. Wówczas pojazdy tej linii wyruszają z przystanku
p1
o godzinie g minut 0, 15, 30, 45, gdzie
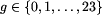 . Podobnie, czasy odjazdu z
przystanku p2 są równe godzina g minut
. Podobnie, czasy odjazdu z
przystanku p2 są równe godzina g minut 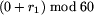 ,
,
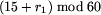 ,
,
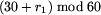 ,
, 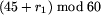 , gdzie r1 jest czasem
przejazdu od przystanku p1 do p2.
Tak więc, zapamiętanie rozkładu jazdy na dowolnym przystanku wymaga
przechowania jednej z chwil odjazdów wyrażonej jako liczba minut po
(dowolnej) godzinie g (pozostałe chwile odjazdów
można łatwo obliczyć znając
częstotliwość kursowania linii). Dane określające rozkład jazdy dla
dowolnego przystanku pi\/ można przechować w rekordach o postaci:
, gdzie r1 jest czasem
przejazdu od przystanku p1 do p2.
Tak więc, zapamiętanie rozkładu jazdy na dowolnym przystanku wymaga
przechowania jednej z chwil odjazdów wyrażonej jako liczba minut po
(dowolnej) godzinie g (pozostałe chwile odjazdów
można łatwo obliczyć znając
częstotliwość kursowania linii). Dane określające rozkład jazdy dla
dowolnego przystanku pi\/ można przechować w rekordach o postaci:
| 1 | type dane_odj = { dane dotyczące odjazdów z przystanku pi } |
| 2 | record |
| 3 | pi: integer; { pi - przystanek aktualny } |
| 4 | pj: integer; { pj - przystanek następny (sąsiedni) } |
| 5 | r: byte; { ``czysty'' czas przejazdu od przystanku } |
| 6 | { pi do pj } |
| 7 | go: byte; { jedna z chwil odjazdów pamiętana jako liczba } |
| 8 | { minut po (dowolnej) godzinie g } |
| 9 | c: byte; { częstotliwość kursowania pojazdów linii, } |
| 10 | { której dotyczy niniejszy rekord } |
| 11 | end; |
zaś cały rozkład jazdy w tablicy: xxx\=xx\=xx\=xx\=xx\=xx\=xx\=xx\=xx\=xx\=xx\=
\> rozkl_jazdy\/: array[1 .. q] of dane_odj\/; gdzie q\/ jest całkowitą liczbą rekordów. Zauważmy, że dla dowolnego przystanku pi\/, z wyjątkiem przystanków krańcowych, liczba rekordów w rozkładzie jazdy jest równa podwojonej liczbie linii komunikacyjnych (bo linie prowadzą w obie strony), których pojazdy dojeżdżają, a następnie odjeżdżają z tego przystanku. Dla przystanków krańcowych liczba rekordów jest równa liczbie linii komunikacyjnych wychodzących z tych przystanków. Dla przykładowej sieci z treści zadania, q=12. Liczby rekordów w rozkładzie jazdy dla wierzchołków od 1 do 6 są równe, odpowiednio, 1, 1, 4, 4, 1 oraz 1.
Zadanie można rozwiązać adaptując do tego celu algorytm Dijkstry znajdowania najkrótszych dróg w grafie (zobacz [14]). W naszym przypadku czas przejazdu między przystankami nie jest stały i zależy od chwili h\/, w której przybywamy na przystanek. Znając chwilę h\/, przystanki pi\/, pj\/ oraz linię komunikacyjną, którą podróżujemy (tj. odpowiedni rekord w tablicy rozkl_jazdy\/), czas przejazdu pomiędzy przystankami pi\/ oraz pj\/ można wyznaczyć za pomocą funkcji:
| 1 | function{\it czas_przejazdu\/}({\it pi\/}, {\it pj\/}: {\it integer\/}; h: {\it integer\/}): {\it integer\/}; |
| 2 | begin |
| 3 | {\it czas_przejazdu\/} := (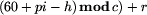 ; ; |
| 4 | end |
Wartość 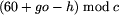 jest czasem
oczekiwania na przystanku
pi\/, zaś r\/ jest ``czystym'' czasem przejazdu wybraną linią od
przystanku pi\/ do pj\/.
jest czasem
oczekiwania na przystanku
pi\/, zaś r\/ jest ``czystym'' czasem przejazdu wybraną linią od
przystanku pi\/ do pj\/.
Stosując algorytm Dijkstry do rozwiązania naszego zadania będziemy wyróżniać wśród wszystkich przystanków sieci te z nich, dla których najkrótszy czas dojazdu z przystanku początkowego x został już ustalony. Do tego celu wprowadzimy tablicę: xxx\=xx\=xx\=xx\=xx\=xx\=xx\=xx\=xx\=xx\=xx\=
\> ustal\/: array[1 .. n] of boolean; w której wartość ustal\/[i] = true\/, i=1, 2, ..., n, oznacza, że znamy już najkrótszy czas dojazdu od przystanku x do i. Początkowo inicjujemy wszystkie elementy na false\/, za wyjątkiem elementu ustal\/[x], któremu przypisujemy wartość true\/. Będziemy także korzystać z tablicy: xxx\=xx\=xx\=xx\=xx\=xx\=xx\=xx\=xx\=xx\=xx\=
\> D\/: array[1 .. n] of integer\,;
w której zapamiętamy najkrótsze czasy dojazdu wyrażone
w minutach od przystanku x do przystanku i, i=1, 2, ..., n,
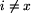 . Elementy tablicy inicjujemy wartością
. Elementy tablicy inicjujemy wartością 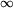 , za wyjątkiem
przystanku x, dla którego przyjmujemy D[x]=0.
Oto rozwiązanie naszego zadania:
, za wyjątkiem
przystanku x, dla którego przyjmujemy D[x]=0.
Oto rozwiązanie naszego zadania:
| 1 | D[x] := 0; { przyjęcie czasu dojazdu do przystanku x jako równego 0 } |
| 2 | for k := 1 to n do |
| 3 | { W każdej iteracji ustalany jest najkrótszy czas przejazdu } |
| 4 | { z przystanku x do jednego z przystanków sieci. } |
| 5 | Znajdź indeks w taki, że D[w] jest minimalne wśród wszystkich |
| 6 | D[i], i = 1, 2, ..., n, dla których ustal[i] = false; |
| 7 | if D[w] = 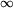 then then |
| 8 | Nie istnieje ścieżka do przystanku końcowego; break; |
| 9 | end if; |
| 10 | ustal[w] := true; |
| 11 | if w = y then |
| 12 | break; { Zadanie rozwiązano; wynik: D[w]=D[y] } |
| 13 | end if; |
| 14 | for wszystkich połączeń (w, i) między sąsiednimi przystankami |
| 15 | w oraz i, dla których ustal[i] = false do |
| 16 | a :=czas_przejazdu(w, i, (mx+D[w]) mod 60); |
| 17 | if 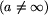 and (D[w]+a<D[i]) then and (D[w]+a<D[i]) then |
| 18 | D[i] := D[w]+a; |
| 19 | end if; |
| 20 | end for; |
| 21 | end for; |
| 22 | t := gx*60+mx+D[y]; |
| 23 | writeln((t div 60) mod 24, ' ', t mod 60); |
W każdej iteracji instrukcji for w wierszach 2-21 zostaje dołączony jeden przystanek, dla którego zostaje ustalony minimalny czas dojazdu z przystanku początkowego x. Przystanek ten, o indeksie w, ma najkrótszy czas dojazdu D[w] przez wszystkie przystanki, dla których najkrótsze czasy zostały już ustalone. W wierszach 14-20 sprawdzamy czy po dołączeniu przystanku w, czasy dojazdu do pozostałych przystanków o nieustalonym czasie dojazdu przez przystanek w nie uległy skróceniu. Jeżeli tak, to czasy te modyfikujemy.
Złożoność czasowa poprawiania tablicy D (wiersze 14-20) jest O(q), gdzie q jest liczbą rekordów w tablicy rozkl_jazdy\/. Złożoność czasowa n-krotnego wyszukiwania minimalnej wartości D[w] jest O(n2)
W efektywnej implementacji algorytmu warto jest pogrupować rekordy tablicy rozkl_jazdy\/ według numerów przystanków odjazdu, ponieważ uaktualniając tablicę D (wiersze 14-20) przeglądamy połączenia wychodzące z przystanku w. Numery przystanków są liczbami całkowitymi z zakresu 1 .. n, więc grupowanie takie można zrealizować za pomocą sortowania pozycyjnego z użyciem liczników częstości w czasie O(n+q) (zobacz [11]). Podsumowując, złożoność czasowa przedstawionego rozwiązania jest O(n2+q).
Do generowania losowych testów użyto generatora gen_pod.pas, który losuje zestaw danych o zadanych parametrach (bez gwarancji, że rozwiązanie istnieje). Ręcznie zadano stacje końcowe tak, żeby rozwiązanie było znajdowane pod koniec przeszukiwania.