| Wojciech Guzicki | Marek Pawlicki |
| Treść zadania, Opracowanie | Program wzorcowy |
Przedziały
Dany jest ciąg n przedziałów domkniętych
[ ai; bi ], gdzie i=1,2,...,n.
Suma tych przedziałów może być przedstawiona
w postaci sumy parami rozłącznych przedziałów domkniętych.
Zadanie polega na znalezieniu przedstawienia tej sumy
w postaci sumy minimalnej liczby parami rozłącznych przedziałów
domkniętych.
Przedziały tworzące to przedstawienie należy zapisać w pliku
wyjściowym w rosnącej kolejności.
Mówimy, że dwa przedziały rozłączne [ a; b]
i [ c; d] są ustawione w rosnącej kolejności wtedy
i tylko wtedy, gdy 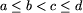 .
.
Zadanie
Napisz program, który:
- wczyta z pliku tekstowego prz.in opis ciągu
przedziałów,
- wyznaczy parami rozłączne przedziały
spełniające warunki zadania,
- zapisze wyznaczone przedziały w
rosnącej kolejności do pliku tekstowego prz.out .
Wejście
W pierwszym wierszu pliku tekstowego prz.in znajduje
się jedna liczba całkowita n, spełniająca nierówności
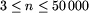 .
Jest to liczba przedziałów. W (i+1)-szym wierszu pliku,
.
Jest to liczba przedziałów. W (i+1)-szym wierszu pliku,
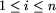 , znajduje się opis przedziału
[ ai; bi ] w postaci dwóch
liczb całkowitych ai i bi oddzielonych pojedynczym
odstępem, będących odpowiednio jego początkiem i końcem,
, znajduje się opis przedziału
[ ai; bi ] w postaci dwóch
liczb całkowitych ai i bi oddzielonych pojedynczym
odstępem, będących odpowiednio jego początkiem i końcem,
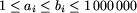 .
.
Wyjście
W kolejnych wierszach pliku tekstowego prz.out należy
zapisać opisy znalezionych parami rozłącznych przedziałów.
W każdym wierszu ma być zapisany opis jednego przedziału w
postaci dwóch liczb całkowitych oddzielonych pojedynczym odstępem,
będących odpowiednio początkiem i końcem tego przedziału.
Przedziały w pliku wyjściowym powinny
być zapisane w rosnącej kolejności.
Przykład
Dla pliku wejściowego prz.in
5
5 6
1 4
10 10
6 9
8 10
poprawną odpowiedzią jest plik wyjściowy prz.out
1 4
5 10
Rozwiązanie
Przedziały [ ai;bi ] sortujemy w
kolejności wzrastania początków. Jako bieżący bierzemy
pierwszy przedział. Niech będzie to przedział [a;b].
Niech kolejnym przedziałem będzie [c;d].
Jeśli 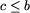 i d > b, to modyfikujemy przedział
bieżący: będzie nim odtąd [a;d]. Jeśli
natomiast c>b, to zapisujemy przedział bieżący, a
nowym przedziałem bieżącym będzie odtąd [c;d].
Po wyczerpaniu wszystkich przedziałów
zapisujemy przedział bieżący.
i d > b, to modyfikujemy przedział
bieżący: będzie nim odtąd [a;d]. Jeśli
natomiast c>b, to zapisujemy przedział bieżący, a
nowym przedziałem bieżącym będzie odtąd [c;d].
Po wyczerpaniu wszystkich przedziałów
zapisujemy przedział bieżący.
Załóżmy, że dane o przedziałach zostały zapisane w
tablicy P następującej postaci:
| 1 | type |
| 2 | Przedzial=record |
| 3 | Poczatek,Koniec : longint; |
| 4 | end |
| 5 | Przedzialy=array[1..n] of Przedzial; |
| 6 | |
| 7 | var |
| 8 | P:Przedzialy; |
Załóżmy następnie, że tablica P jest już
posortowana w kolejności wzrastania początków. Opisany
wyżej algorytm można zapisać w postaci następującego
fragmentu programu:
| 1 | Biezacy:= P[1]; |
| 2 | for i:= 2 to n do |
| 3 | if (P[i].Poczatek  Biezacy.Koniec) Biezacy.Koniec) |
| 4 | and (P[i].Koniec > Biezacy.Koniec) then |
| 5 | Biezacy.Koniec := P[i].Koniec |
| 6 | end if P[i].Poczatek > Biezacy.Koniec then begin |
| 7 | Zapisz(Biezacy); |
| 8 | Biezacy:= P[i] |
| 9 | end; |
| 10 | Zapisz(Biezacy); |
Procedura Zapisz zapisuje dane o przedziale
Biezacy do pliku wyjściowego.
Jak widać, zadanie to jest dość łatwe. Jednak przy
implementacji tego prostego algorytmu mogą wystąpić
pewne trudności. Spróbujemy je teraz omówić.
- Czas działania programu zależy od wyboru
procedury sortującej. Nie będziemy tu omawiać różnych
sposobów sortowania; algorytmy sortujące były
wielokrotnie opisywane w sprawozdaniach z wcześniejszych
Olimpiad Informatycznych, można też je znaleźć w wielu
popularnych podręcznikach. Wspomnimy tu tylko o tym, że
wybór wolno działającej procedury sortującej (np.
sortowanie przez wybieranie, sortowanie przez wstawianie,
sortowanie bąbelkowe - działających w czasie O(n2))
spowoduje przekroczenie dopuszczalnego limitu czasu dla
danych zapisanych w plikach PRZ7.IN i PRZ8.IN.
Zadanie można też rozwiązać z pominięciem sortowania,
dołączając kolejny przedział w odpowiednim miejscu do
aktualnej listy przedziałów parami rozłącznych. Taki
program też będzie działał na ogół w czasie
O(n2). Testy sprawdzające zostały dobrane w taki
sposób, by odróżnić rozwiązania wykorzystujące
sortowanie w czasie kwadratowym od rozwiązań
wykorzystujących sortowanie w czasie
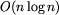 (sortowanie szybkie lub sortowanie stogowe) lub sortowanie
w czasie O(n) (sortowanie pozycyjne). Program wzorcowy
PRZ.PAS używa właśnie sortowania pozycyjnego.
(sortowanie szybkie lub sortowanie stogowe) lub sortowanie
w czasie O(n) (sortowanie pozycyjne). Program wzorcowy
PRZ.PAS używa właśnie sortowania pozycyjnego.
- Druga trudność polega na braku pamięci. Jeśli
dysponujemy kompilatorem dopuszczającym używanie dowolnie
długich tablic, to z tą trudnością się nie zetkniemy.
Jeśli jednak użyjemy np. kompilatora Turbo Pascala,
to nie będziemy mogli zadeklarować jednej tablicy
zawierającej dane o wszystkich przedziałach. Mianowicie
początek i koniec każdego przedziału jest liczbą typu
longint; zajmuje więc 4 bajty. Dane o każdym przedziale
zajmują więc 8 bajtów. Maksymalna liczba przedziałów
(50 tysięcy) będzie wymagać 400\,000 bajtów. Te dane
musimy zapisać w kilku tablicach, używając do tego
zmiennych dynamicznych. Można teraz wybrać jedno z kilku
rozwiązań. Pierwsze polega na posortowaniu każdej
tablicy oddzielnie i wybieraniu jako kolejnego przedziału
najmniejszego z przedziałów najmniejszych w tych
tablicach (podobnie jak czyni się to w procedurze
sortowania przez łączenie). Drugie rozwiązanie polega na
traktowaniu tych kilku tablic jak jednej długiej tablicy.
Zamiast odwołania P[i] do i-tego miejsca w
tablicy P musimy teraz za każdym razem
obliczyć, do którego miejsca w której tablicy się
odwołujemy. Zaprogramowanie jednoczesnego sortowania
takich tablic wymaga trochę staranności, ale nie jest
bardzo trudne.
Do tego zadania ułożono 8 testów:
- prz1.in: trzy przedziały [1;1];
- prz2.in: 10 przedziałów
zachodzących na siebie;
- prz3.in: 10 przedziałów
rozłącznych, zapisanych w odwrotnej kolejności;
- prz4.in: 20 przedziałów takich,
że każdy następny zawiera poprzedni;
- prz5.in: 6 przedziałów
stykających się brzegami;
- prz6.in: 1000 losowo wybranych
przedziałów;
- prz7.in: 20000 losowo wybranych
przedziałów;
- prz8.in: 50000 losowo wybranych
przedziałów.
Wszystkie rozwiązania poprawne (również działające w
czasie kwadratowym) przechodziły przez testy od 1 do 6;
przez ostatnie dwa testy przechodziły tylko programy
wykorzystujące szybsze algorytmy sortowania.
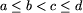 .
.
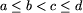 .
.
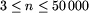 .
Jest to liczba przedziałów. W (i+1)-szym wierszu pliku,
.
Jest to liczba przedziałów. W (i+1)-szym wierszu pliku,
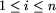 , znajduje się opis przedziału
[ ai; bi ] w postaci dwóch
liczb całkowitych ai i bi oddzielonych pojedynczym
odstępem, będących odpowiednio jego początkiem i końcem,
, znajduje się opis przedziału
[ ai; bi ] w postaci dwóch
liczb całkowitych ai i bi oddzielonych pojedynczym
odstępem, będących odpowiednio jego początkiem i końcem,
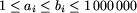 .
.
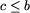 i d > b, to modyfikujemy przedział
bieżący: będzie nim odtąd [a;d]. Jeśli
natomiast c>b, to zapisujemy przedział bieżący, a
nowym przedziałem bieżącym będzie odtąd [c;d].
Po wyczerpaniu wszystkich przedziałów
zapisujemy przedział bieżący.
i d > b, to modyfikujemy przedział
bieżący: będzie nim odtąd [a;d]. Jeśli
natomiast c>b, to zapisujemy przedział bieżący, a
nowym przedziałem bieżącym będzie odtąd [c;d].
Po wyczerpaniu wszystkich przedziałów
zapisujemy przedział bieżący.
 Biezacy.Koniec)
Biezacy.Koniec)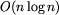 (sortowanie szybkie lub sortowanie stogowe) lub sortowanie
w czasie O(n) (sortowanie pozycyjne). Program wzorcowy
PRZ.PAS używa właśnie sortowania pozycyjnego.
(sortowanie szybkie lub sortowanie stogowe) lub sortowanie
w czasie O(n) (sortowanie pozycyjne). Program wzorcowy
PRZ.PAS używa właśnie sortowania pozycyjnego.