| Wojciech Rytter | Piotr Sankowski |
| Treść zadania, Opracowanie | Program wzorcowy |
Spokojna komisja
W parlamencie Demokratycznej Republiki Bajtocji,
zgodnie z Bardzo Ważną Ustawą, należy
ukonstytuować Komisję Poselską do Spraw Spokoju Publicznego.
Niestety sprawę utrudnia fakt, iż niektórzy posłowie wzajemnie się nie lubią.
Komisja musi spełniać następujące warunki:
- każda partia ma dokładnie jednego reprezentanta w Komisji,
- jeśli dwaj posłowie się nie lubią, to nie mogą jednocześnie być
w Komisji.
Każda partia ma w parlamencie dokładnie dwóch posłów.
Wszyscy posłowie są ponumerowani liczbami od 1 do 2n.
Posłowie o numerach 2i-1 i 2i należą do partii o numerze i.
Zadanie
Napisz program, który:
- wczyta z pliku tekstowego spo.in liczbę partii oraz pary posłów,
którzy się wzajemnie nie lubią,
- wyznaczy skład Komisji, lub
stwierdzi, że nie da się jej ukonstytuować,
- zapisze wynik w pliku tekstowym spo.out.
Wejście
W pierwszym wierszu pliku tekstowego spo.in znajdują się dwie
nieujemne liczby całkowite n i m.
Liczba n, spełniająca warunki  ,
oznacza liczbę partii. Liczba m, spełniająca warunki
,
oznacza liczbę partii. Liczba m, spełniająca warunki 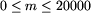 ,
oznacza liczbę par nielubiących się posłów.
W każdym z kolejnych m wierszy zapisana jest para liczb
naturalnych a i b,
,
oznacza liczbę par nielubiących się posłów.
W każdym z kolejnych m wierszy zapisana jest para liczb
naturalnych a i b, 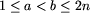 , oddzielonych
pojedynczym odstępem. Oznacza ona, że posłowie o numerach a i b
wzajemnie się nie lubią.
, oddzielonych
pojedynczym odstępem. Oznacza ona, że posłowie o numerach a i b
wzajemnie się nie lubią.
Wyjście
Plik tekstowy spo.out powinien zawierać
pojedyncze słowo NIE, jeśli utworzenie Komisji nie jest możliwe.
W przypadku, gdy utworzenie Komisji jest możliwe, plik spo.out
powinien zawierać n liczb całkowitych z przedziału od 1 do 2n,
zapisanych w kolejności rosnącej i oznaczających
numery posłów zasiadających w Komisji. Każda z tych liczb powinna
zostać zapisana w osobnym wierszu. Jeśli Komisję można utworzyć
na wiele sposobów, Twój program może wypisać dowolny z nich.
Przykład
Dla pliku wejściowego spo.in
3 2
1 3
2 4
poprawną odpowiedzią jest plik wyjściowy spo.out
1
4
5
Rozwiązanie
Niech X będzie zbiorem par posłów, którzy się wzajemnie nie lubią.
Potraktujmy X jako krawędzie grafu nieskierowanego, a taki graf
nazwijmy grafem konfliktowym.
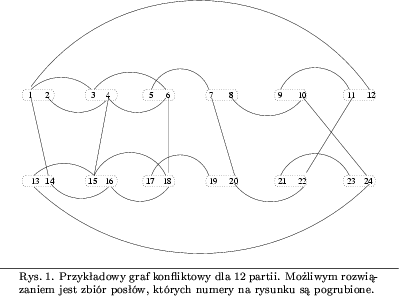
Przykład grafu konfliktowego ilustruje rysunek 1. Pogrubione numery
oznaczają pewien zbiór posłów stanowiący ``spokojną''
Komisję.
Z grafem konfliktowym stowarzyszymy graf 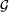 ,
który nazwiemy
grafem wymuszeń. Jeśli x-y
,
który nazwiemy
grafem wymuszeń. Jeśli x-y 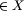 oraz
oraz 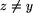 należy do tej samej
partii co y, to
należy do tej samej
partii co y, to 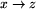 jest skierowaną krawędzią
w grafie wymuszeń.
Oznaczmy
jest skierowaną krawędzią
w grafie wymuszeń.
Oznaczmy
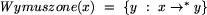
,
gdzie 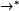 oznacza, że w G można przejść z x do y
po strzałkach.
oznacza, że w G można przejść z x do y
po strzałkach.
Zbiór 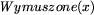 składa się z posłów,
których obecność w komisji jest wymuszona przez obecność w niej
posła x. Zbiory tego typu mają następującą własność.
składa się z posłów,
których obecność w komisji jest wymuszona przez obecność w niej
posła x. Zbiory tego typu mają następującą własność.
Jeśli K jest spokojną Komisją i 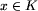 , to
, to 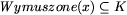 .
.
 Posła x nazwiemy kłopotliwym, jeśli zbiór
Posła x nazwiemy kłopotliwym, jeśli zbiór 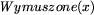 zawiera dwóch posłów z tej samej partii (co jest niedozwolone).
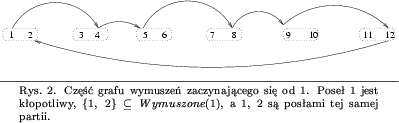
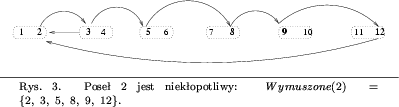
Na rysunku 2 (dla grafu konfliktowego z rysunku 1)
poseł 1 jest kłopotliwy, natomiast poseł 2 z rysunku 3
jest niekłopotliwy.
zawiera dwóch posłów z tej samej partii (co jest niedozwolone).
Na rysunku 2 (dla grafu konfliktowego z rysunku 1)
poseł 1 jest kłopotliwy, natomiast poseł 2 z rysunku 3
jest niekłopotliwy.
W celu sformowania Komisji wykonujemy następujący algorytm:
Algorytm KOMISJA1;
początkowo zbiorem reprezentantów jest  ; ;
while 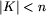 do do
begin
niech  będzie pierwszą partią bez reprezentanta w K; będzie pierwszą partią bez reprezentanta w K;
if obaj posłowie należący do  są kłopotliwi then są kłopotliwi then
nie ma rozwiązania, STOP
else
begin
wybierz pierwszego niekłopotliwego posła 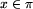 ; ;
K := 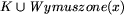
end
end
return K;
|
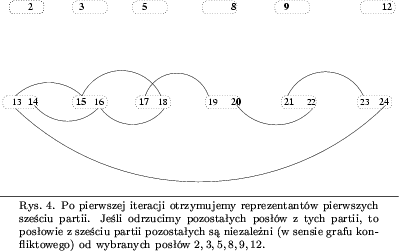
Zobaczmy jak działa ten algorytm na naszym przykładzie (Rys. 4).
Na początku wybieramy pierwszą partię. Poseł 1 jest kłopotliwy, zatem
wybieramy posła 2. 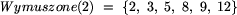 .
Zbiorem K staje się
.
Zbiorem K staje się 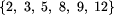 .
Następną partią bez reprezentanta jest
.
Następną partią bez reprezentanta jest 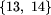 . Poseł 13 jest
kłopotliwy, dodajemy do K zbiór
. Poseł 13 jest
kłopotliwy, dodajemy do K zbiór 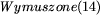 . Otrzymujemy
końcowy rezultat.
. Otrzymujemy
końcowy rezultat.
Dowód poprawności.
Algorytm wybiera reprezentanta x z pierwszej partii, a następnie
tworzy 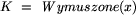 . Partie bez reprezentantów w K
są, w sensie grafu konfliktowego, całkowicie niezależne od K (zobacz
rysunek 4).
. Partie bez reprezentantów w K
są, w sensie grafu konfliktowego, całkowicie niezależne od K (zobacz
rysunek 4).
Własność niezależności.
Niech 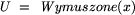 i niech W będzie sumą teoriomnogościową
partii, które są rozłączne z U.
Jeśli x jest niekłopotliwy, to w grafie konfliktowym nie ma krawędzi między U i W.
i niech W będzie sumą teoriomnogościową
partii, które są rozłączne z U.
Jeśli x jest niekłopotliwy, to w grafie konfliktowym nie ma krawędzi między U i W.
Algorytm znajduje reprezentantów dla pozostałych partii, tak jak
gdyby startował od początku. Formalnie poprawność można wykazać
indukcyjnie ze względu na liczbę partii.
Zamiast umieszczać w komisji K grupy posłów możemy powiększać
komisję po jednym pośle, stosując następującą wersję algorytmu KOMISJA1.
Jest to wersja łatwiejsza do zaprogramowania, natomiast poprzednia wersja
jest łatwiejsza z punktu widzenia poprawności.
W tej wersji dostaniemy dokładnie tę samą komisję.
Oznaczmy i-tą partię przez 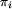 . Powiemy, że
poseł x jest zgodny ze zbiorem posłów w K, gdy x
nie jest w konflikcie z żadnym z posłów w K.
. Powiemy, że
poseł x jest zgodny ze zbiorem posłów w K, gdy x
nie jest w konflikcie z żadnym z posłów w K.
Algorytm KOMISJA;
początkowo zbiorem reprezentantów jest  ; ;
for i := 1 to n do
begin
wybierz pierwszego niekłopotliwego posła 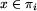 zgodnego z K; zgodnego z K;
if nie ma takiego posła then nie ma rozwiązania, STOP;
K := 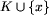
end
return K;
|
Algorytm Komisja zaimplementowany bezpośrednio może działać zbyt wolno.
Sprawdzenie, czy poseł jest niekłopotliwy może wymagać czasu proporcjonalnego
do rozmiaru grafu wymuszeń. Zatem łączny czas działania algorytmu wynosi
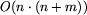 . W programie wzorcowym Komisja wybierana jest trochę
sprytniej.
Rozpoczynamy od znalezienia w grafie wymuszeń wszystkich silnie spójnych
składowych, czyli podgrafów, w których od każdego wierzchołka można
przejść do każdego innego wierzchołka idąc po strzałkach. Silnie spójne składowe można znaleźć w czasie proporcjonalnym do rozmiaru grafu (zobacz [11]).
Jeśli istnieje choć jedna silnie spójna składowa zawierająca posłów z tej samej
partii, to oczywiście ``spokojnej'' Komisji nie da się sformować. W przeciwnym
przypadku patrzymy na graf silnie spójnych składowych - wierzchołkami są
silnie silnie spójne składowe, a od składowej A prowadzi krawędź do B tylko wtedy, gdy w wyjściowym grafie istnieje krawędź od pewnego wierzchołka z A do pewnego wierzchołka z B. Następnie silnie spójne składowe sortujemy topologicznie
i rozważamy je w otrzymanej kolejności.
Jeśli aktualnie rozważana silnie spójna składowa nie została wcześniej odrzucona,
to wybieramy wszystkich należących do niej posłów do Komisji.
Dla każdego wybranego w ten sposób posła, odrzucamy silnie spójną składową, która
zawiera jego partyjnego kolegę, oraz wszystkie składowe, z których ta składowa
jest osiągalna. Jeśli w ten sposób wybierzemy n posłów odpowiadamy TAK, a
przeciwnym razie NIE.
. W programie wzorcowym Komisja wybierana jest trochę
sprytniej.
Rozpoczynamy od znalezienia w grafie wymuszeń wszystkich silnie spójnych
składowych, czyli podgrafów, w których od każdego wierzchołka można
przejść do każdego innego wierzchołka idąc po strzałkach. Silnie spójne składowe można znaleźć w czasie proporcjonalnym do rozmiaru grafu (zobacz [11]).
Jeśli istnieje choć jedna silnie spójna składowa zawierająca posłów z tej samej
partii, to oczywiście ``spokojnej'' Komisji nie da się sformować. W przeciwnym
przypadku patrzymy na graf silnie spójnych składowych - wierzchołkami są
silnie silnie spójne składowe, a od składowej A prowadzi krawędź do B tylko wtedy, gdy w wyjściowym grafie istnieje krawędź od pewnego wierzchołka z A do pewnego wierzchołka z B. Następnie silnie spójne składowe sortujemy topologicznie
i rozważamy je w otrzymanej kolejności.
Jeśli aktualnie rozważana silnie spójna składowa nie została wcześniej odrzucona,
to wybieramy wszystkich należących do niej posłów do Komisji.
Dla każdego wybranego w ten sposób posła, odrzucamy silnie spójną składową, która
zawiera jego partyjnego kolegę, oraz wszystkie składowe, z których ta składowa
jest osiągalna. Jeśli w ten sposób wybierzemy n posłów odpowiadamy TAK, a
przeciwnym razie NIE.
Testy
Zadanie testowane było na zestawie 13 danych testowych:
- spo1.in - mały test poprawnościowy;
- spo2.in - mały test poprawnościowy;
- spo3.in - średni test poprawnościowy;
- spo4a.in - średni test z odpowiedzią NIE, dla którego ``backtracking'' działa
wykładniczo;
- spo4b.in - średni test wydajnościowy, dla którego komisja daje się sformować;
- spo5a.in - średni test z odpowiedzią NIE, dla którego ``backtracking'' działa
wykładniczo;
- spo5b.in - średni test, dla którego komisja daje się sformować;
- spo6a.in - duży test z odpowiedzią NIE, dla którego ``backtracking'' działa
wykładniczo;
- spo6b.in - duży test, dla którego komisja istnieje;
- spo7.in - test o maksymalnym rozmiarze;
- spo8a.in - duży test, dla którego rozwiązanie KOMISJA działa w czasie O(n2);
- spo8b.in - duży test, dla którego rozwiązanie KOMISJA działa w czasie O(n2) (trochę inny wariant);
- spo8c.in - duży test losowy z odpowiedzią TAK.
Testy 4a i 4b, 5a i 5b, 6a i 6b oraz 8a, 8b i 8c były zgrupowane.
 ,
oznacza liczbę partii. Liczba m, spełniająca warunki
,
oznacza liczbę partii. Liczba m, spełniająca warunki 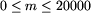 ,
oznacza liczbę par nielubiących się posłów.
W każdym z kolejnych m wierszy zapisana jest para liczb
naturalnych a i b,
,
oznacza liczbę par nielubiących się posłów.
W każdym z kolejnych m wierszy zapisana jest para liczb
naturalnych a i b, 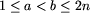 , oddzielonych
pojedynczym odstępem. Oznacza ona, że posłowie o numerach a i b
wzajemnie się nie lubią.
, oddzielonych
pojedynczym odstępem. Oznacza ona, że posłowie o numerach a i b
wzajemnie się nie lubią.
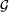 ,
który nazwiemy
grafem wymuszeń. Jeśli x-y
,
który nazwiemy
grafem wymuszeń. Jeśli x-y 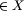 oraz
oraz 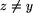 należy do tej samej
partii co y, to
należy do tej samej
partii co y, to 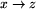 jest skierowaną krawędzią
w grafie wymuszeń.
Oznaczmy
jest skierowaną krawędzią
w grafie wymuszeń.
Oznaczmy 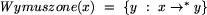 ,
,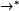 oznacza, że w G można przejść z x do y
po strzałkach.
oznacza, że w G można przejść z x do y
po strzałkach.
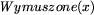 składa się z posłów,
których obecność w komisji jest wymuszona przez obecność w niej
posła x. Zbiory tego typu mają następującą własność.
składa się z posłów,
których obecność w komisji jest wymuszona przez obecność w niej
posła x. Zbiory tego typu mają następującą własność.
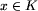 , to
, to 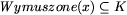 .
.



 ;
;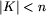 do
do będzie pierwszą partią bez reprezentanta w K;
będzie pierwszą partią bez reprezentanta w K;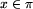 ;
;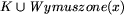

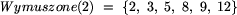 .
Zbiorem K staje się
.
Zbiorem K staje się 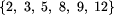 .
Następną partią bez reprezentanta jest
.
Następną partią bez reprezentanta jest 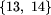 . Poseł 13 jest
kłopotliwy, dodajemy do K zbiór
. Poseł 13 jest
kłopotliwy, dodajemy do K zbiór 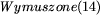 . Otrzymujemy
końcowy rezultat.
. Otrzymujemy
końcowy rezultat.
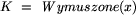 . Partie bez reprezentantów w K
są, w sensie grafu konfliktowego, całkowicie niezależne od K (zobacz
rysunek 4).
. Partie bez reprezentantów w K
są, w sensie grafu konfliktowego, całkowicie niezależne od K (zobacz
rysunek 4).
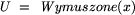 i niech W będzie sumą teoriomnogościową
partii, które są rozłączne z U.
Jeśli x jest niekłopotliwy, to w grafie konfliktowym nie ma krawędzi między U i W.
i niech W będzie sumą teoriomnogościową
partii, które są rozłączne z U.
Jeśli x jest niekłopotliwy, to w grafie konfliktowym nie ma krawędzi między U i W.
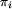 . Powiemy, że
poseł x jest zgodny ze zbiorem posłów w K, gdy x
nie jest w konflikcie z żadnym z posłów w K.
. Powiemy, że
poseł x jest zgodny ze zbiorem posłów w K, gdy x
nie jest w konflikcie z żadnym z posłów w K.
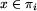 zgodnego z K;
zgodnego z K;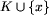
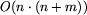 . W programie wzorcowym Komisja wybierana jest trochę
sprytniej.
Rozpoczynamy od znalezienia w grafie wymuszeń wszystkich silnie spójnych
składowych, czyli podgrafów, w których od każdego wierzchołka można
przejść do każdego innego wierzchołka idąc po strzałkach. Silnie spójne składowe można znaleźć w czasie proporcjonalnym do rozmiaru grafu (zobacz [11]).
Jeśli istnieje choć jedna silnie spójna składowa zawierająca posłów z tej samej
partii, to oczywiście ``spokojnej'' Komisji nie da się sformować. W przeciwnym
przypadku patrzymy na graf silnie spójnych składowych - wierzchołkami są
silnie silnie spójne składowe, a od składowej A prowadzi krawędź do B tylko wtedy, gdy w wyjściowym grafie istnieje krawędź od pewnego wierzchołka z A do pewnego wierzchołka z B. Następnie silnie spójne składowe sortujemy topologicznie
i rozważamy je w otrzymanej kolejności.
Jeśli aktualnie rozważana silnie spójna składowa nie została wcześniej odrzucona,
to wybieramy wszystkich należących do niej posłów do Komisji.
Dla każdego wybranego w ten sposób posła, odrzucamy silnie spójną składową, która
zawiera jego partyjnego kolegę, oraz wszystkie składowe, z których ta składowa
jest osiągalna. Jeśli w ten sposób wybierzemy n posłów odpowiadamy TAK, a
przeciwnym razie NIE.
. W programie wzorcowym Komisja wybierana jest trochę
sprytniej.
Rozpoczynamy od znalezienia w grafie wymuszeń wszystkich silnie spójnych
składowych, czyli podgrafów, w których od każdego wierzchołka można
przejść do każdego innego wierzchołka idąc po strzałkach. Silnie spójne składowe można znaleźć w czasie proporcjonalnym do rozmiaru grafu (zobacz [11]).
Jeśli istnieje choć jedna silnie spójna składowa zawierająca posłów z tej samej
partii, to oczywiście ``spokojnej'' Komisji nie da się sformować. W przeciwnym
przypadku patrzymy na graf silnie spójnych składowych - wierzchołkami są
silnie silnie spójne składowe, a od składowej A prowadzi krawędź do B tylko wtedy, gdy w wyjściowym grafie istnieje krawędź od pewnego wierzchołka z A do pewnego wierzchołka z B. Następnie silnie spójne składowe sortujemy topologicznie
i rozważamy je w otrzymanej kolejności.
Jeśli aktualnie rozważana silnie spójna składowa nie została wcześniej odrzucona,
to wybieramy wszystkich należących do niej posłów do Komisji.
Dla każdego wybranego w ten sposób posła, odrzucamy silnie spójną składową, która
zawiera jego partyjnego kolegę, oraz wszystkie składowe, z których ta składowa
jest osiągalna. Jeśli w ten sposób wybierzemy n posłów odpowiadamy TAK, a
przeciwnym razie NIE.