| Wojciech Guzicki | Andrzej Gąsienica--Samek |
| Treść zadania, Opracowanie | Program wzorcowy |
Na wyspie o kształcie wielokąta wypukłego o 2n bokach, znajduje się 2n-2 państw - trójkątów, których wierzchołki są jednocześnie wierzchołkami wielokąta. Nie ma państw graniczących dokładnie z dwoma innymi państwami (zatem każde państwo graniczy albo tylko z jednym państwem, albo z trzema).
Wynika stąd, że istnieje dokładnie n państw graniczących tylko z jednym państwem (są to państwa nadmorskie) oraz n-2 państw graniczących z trzema sąsiadami (są to państwa wewnątrzlądowe). Państwa nadmorskie są ponumerowane liczbami od 1 do n, natomiast państwa wewnątrzlądowe mają numery od n+1 do 2n-2.
Gdy podróżujemy z jednego państwa do drugiego, to za przekroczenie każdej granicy musimy zapłacić ustaloną stawkę. Poszczególne stawki mogą być różne, ale przekroczenie granicy w obu kierunkach kosztuje tyle samo.
Dla każdych dwóch państw, spośród n państw nadmorskich, znana jest
suma opłat granicznych na drodze prowadzącej (lądem)
od jednego państwa do drugiego
przez najmniejszą liczbę granic.
Zadanie polega na wyznaczeniu wszystkich opłat granicznych na całej wyspie.
Dla każdego państwa nadmorskiego należy podać numer państwa, z
którym ono graniczy, oraz wysokość odpowiedniej opłaty granicznej.
Ponadto, dla każdego z n-2 państw wewnątrzlądowych
należy podać numery trzech państw, z którymi ono graniczy, oraz wysokości
opłat na granicach z tymi państwami.
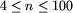 . Jest to liczba państw nadmorskich.
W każdym z następnych n wierszy znajduje się n nieujemnych liczb
całkowitych oddzielonych pojedynczymi odstępami.
Liczba
. Jest to liczba państw nadmorskich.
W każdym z następnych n wierszy znajduje się n nieujemnych liczb
całkowitych oddzielonych pojedynczymi odstępami.
Liczba 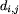 , stojąca na j-tym miejscu w i-tym z tych wierszy,
jest równa sumie opłat granicznych na drodze prowadzącej
(lądem, przez najmniejszą liczbę granic) z państwa
o numerze i do państwa o numerze j.
Zakładamy przy tym, że na każdej granicy opłata graniczna jest liczbą
całkowitą z przedziału [1... 100].
Oczywiście,
, stojąca na j-tym miejscu w i-tym z tych wierszy,
jest równa sumie opłat granicznych na drodze prowadzącej
(lądem, przez najmniejszą liczbę granic) z państwa
o numerze i do państwa o numerze j.
Zakładamy przy tym, że na każdej granicy opłata graniczna jest liczbą
całkowitą z przedziału [1... 100].
Oczywiście, 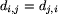 oraz
oraz 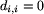 .
.
Dla pliku przykładowego wys.in:
7 0 8 10 8 13 11 14 8 0 8 10 11 5 12 10 8 0 12 5 11 6 8 10 12 0 15 13 16 13 11 5 15 0 14 3 11 5 11 13 14 0 15 14 12 6 16 3 15 0
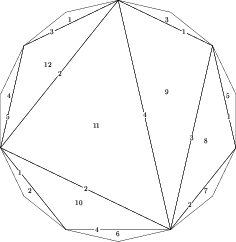
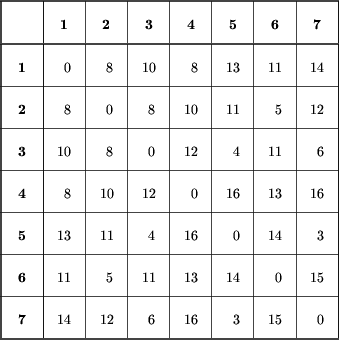
poprawną odpowiedzią jest plik wyjściowy wys.out (zobacz też rysunek obok):
12 3 10 1 9 1 12 5 8 1 10 4 8 2 5 1 7 2 9 3 3 1 8 3 11 4 2 1 6 4 11 2 9 4 10 2 12 2 1 3 4 5 11 2

Będziemy używać terminologii teorii grafów - ułatwi to
zaprezentowanie możliwych algorytmów prowadzących do
rozwiązania zadania. Najprościej mówiąc, grafem
nazywamy skończony zbiór punktów na płaszczyźnie (te
punkty będziemy zaznaczać na rysunku ,,grubymi''
kropkami) oraz pewien zbiór odcinków łączących te
punkty. Wybrane punkty nazywamy wierzchołkami grafu,
wybrane odcinki krawędziami grafu. Te krawędzie
mogą się przecinać, będziemy tylko zakładać, że
punkt przecięcia dwóch krawędzi nie może być
wierzchołkiem grafu. Wierzchołki grafu
będziemy numerować początkowymi liczbami naturalnymi,
zaczynając od 1.
Krawędziom grafu będziemy przyporządkowywać pewne
liczby rzeczywiste. Liczbę rzeczywistą przyporządkowaną
krawędzi łączącej wierzchołki k i l będziemy
nazywać długością tej krawędzi i będziemy
oznaczać symbolem 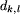 .
.
Liczbę krawędzi wychodzących z jednego wierzchołka
nazywamy stopniem tego wierzchołka.
W naszym przypadku wierzchołki grafu będą odpowiadać
państwom na wyspie. Dwa wierzchołki łączymy
krawędzią, jeśli odpowiadające im państwa graniczą ze
sobą. Wreszcie długością krawędzi będzie koszt
przekraczania granicy. Zauważmy, że w naszym grafie
stopień każdego wierzchołka jest równy 1 (dla państw
nadmorskich) lub 3 (dla państw wewnątrzlądowych). Nasz
graf ma jeszcze jedną ważną własność wynikającą z
geometrii wyspy: nie ma w nim cykli. To znaczy, że nie można
wyjść z jednego wierzchołka, poruszać się po
krawędziach przez inne wierzchołki i powrócić do punktu wyjścia nie przechodząc
przez żaden z wierzchołków więcej niż raz. Ponadto z każdego wierzchołka można
dojść do każdego innego.
Takie grafy nazywamy
drzewami. Jedną z ważnych własności drzew,
wynikającą wprost z tego, że w drzewie nie ma cykli,
jest to, że każde dwa wierzchołki łączy tylko jedna
droga przebiegająca wzdłuż krawędzi. Długość tej
jedynej drogi łączącej wierzchołki k i l (równa
sumie długości krawędzi, przez które ta droga
przebiega) oznaczymy również symbolem 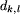 . Jeśli
dwa wierzchołki są połączone krawędzią, to
oczywiście drogą łączącą je jest ta krawędź, a
więc długość tej drogi jest równa długości
krawędzi. Zatem użycie tego samego oznaczenia na
długość krawędzi i długość drogi nie będzie
prowadzić do nieporozumień.
. Jeśli
dwa wierzchołki są połączone krawędzią, to
oczywiście drogą łączącą je jest ta krawędź, a
więc długość tej drogi jest równa długości
krawędzi. Zatem użycie tego samego oznaczenia na
długość krawędzi i długość drogi nie będzie
prowadzić do nieporozumień.
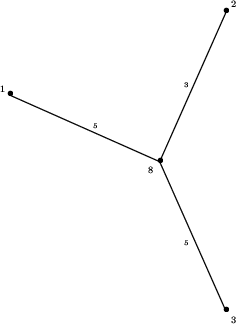
Popatrzmy teraz na przykład. Drzewo odpowiadające wyspie
z treści zadania ma postać:
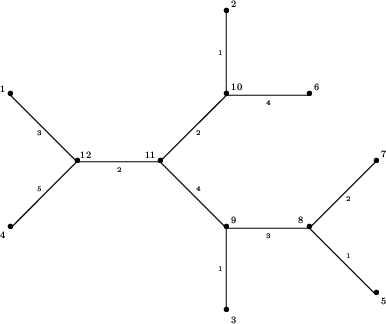
Wierzchołki stopnia 1 nazywamy liśćmi drzewa.
Pozostałe wierzchołki będziemy nazywać węzłami.
Danymi dla zadania są długości dróg łączących liście drzewa. Zadanie polega na tym, by odtworzyć drzewo mając dane wyłącznie odległości między liśćmi. Jest to możliwe dzięki założeniu, że wszystkie węzły mają stopień równy 3. Najprostszy algorytm odtwarzania drzewa polega na znajdowaniu dwóch sąsiednich liści (dwa liście nazywamy sąsiednimi, gdy sąsiadują z tym samym węzłem) i zastępowaniu ich węzłem, z którym sąsiadują. Przypuśćmy, że liście o numerach i oraz j sąsiadują z węzłem o numerze k. Usuwamy z tablicy kosztów wiersze i kolumny o numerach i oraz j i dopisujemy nowy wiersz i nową kolumnę o numerze k. W jaki sposób obliczamy długość drogi z węzła k do dowolnego innego liścia m? Zauważmy, że
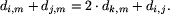
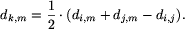
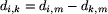
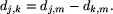
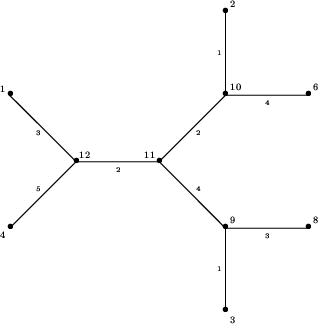
Weźmy sąsiednie liście o numerach 5 i 7. Usuwając je z
drzewa otrzymujemy drzewo mniejsze, w którym mamy nowy
liść o numerze 8:
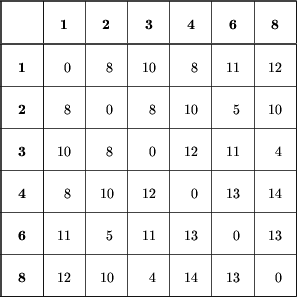
Obliczając długości dróg z liścia 8 do pozostałych
liści według powyższego wzoru, otrzymamy następującą
tabelę długości dróg między liśćmi nowego drzewa:
Teraz znajdujemy następne dwa sąsiednie liście: na
przykład 3 i 8. Usuwamy je z drzewa i do tablicy
długości dróg dopisujemy nowy liść o numerze 9. Nowe
drzewo ma postać:
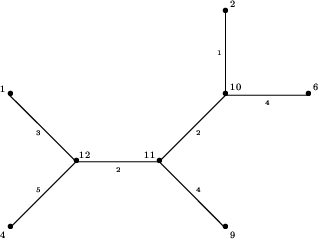
a odpowiednia tabela długości dróg między liśćmi tego drzewa ma postać:
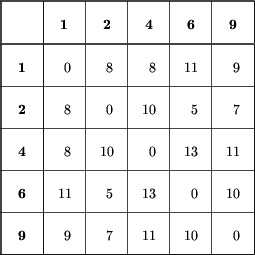
Kontynuujemy to postępowanie. Znajdujemy kolejne
sąsiednie liście: 2 i 6. Usuwamy je z drzewa i z tablicy
długości dróg, dopisując nowy liść o numerze 10.
Otrzymamy następne drzewo i odpowiadającą mu tablicę
długości dróg:
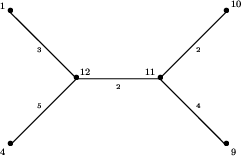
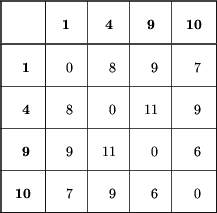
Jeszcze raz usuwamy dwa sąsiednie liście: tym razem o numerach 9 i 10. Dopisujemy nowy liść o numerze 11. Otrzymamy nowe drzewo i odpowiadającą mu tablicę długości dróg:
Mamy teraz drzewo z trzema liśćmi. Ma ono tylko jeden wierzchołek stopnia 3: dajmy mu numer 12. Oczywiście teraz mamy
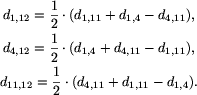
W ten sposób całe drzewo zostało odtworzone. Jedynym
istotnym problemem w tym algorytmie jest to, w jaki sposób
znajdować dwa sąsiednie liście. W powyższym
przykładzie za każdym razem wybieraliśmy dwa liście
położone najbliżej siebie (tzn. liście i oraz j,
dla których liczba 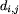 jest najmniejsza). To
udało się tylko dlatego, że drzewo z przykładu zostało
specjalnie dobrane! Ten sposób wybierania sąsiednich
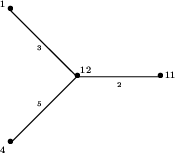
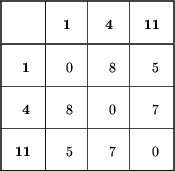
liści na ogół jest niepoprawny. Popatrzmy na inny
przykład drzewa i odpowiadającej mu tabeli odległości:
jest najmniejsza). To
udało się tylko dlatego, że drzewo z przykładu zostało
specjalnie dobrane! Ten sposób wybierania sąsiednich
liści na ogół jest niepoprawny. Popatrzmy na inny
przykład drzewa i odpowiadającej mu tabeli odległości:
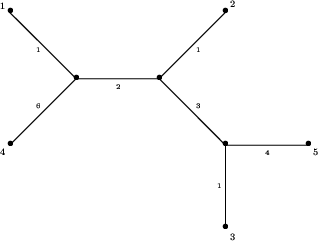
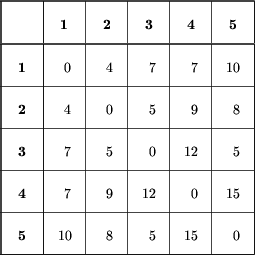
Zauważmy, że najbliżej położone liście (o numerach 1
i 2) nie są sąsiednie! Gdybyśmy mimo to próbowali
zastosować poprzedni algorytm do tej sytuacji,
otrzymalibyśmy kolejno następujące tabele odległości:
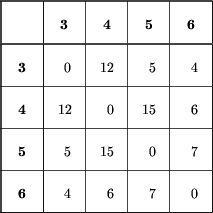
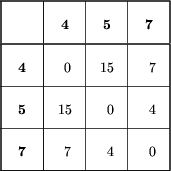
Teraz poprzednie wzory dadzą nam następujące długości krawędzi łączących liście 4, 5 i 7 z wierzchołkiem 8:
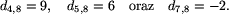
Istnieją dwie metody znajdowania sąsiednich liści. Jedna z nich polega na obliczeniu dla każdego liścia i wielkości
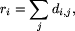
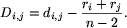
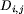 jest
najmniejsza, są sąsiednie.
jest
najmniejsza, są sąsiednie.
Twierdzenie to jest dość sztuczne i nieoczekiwane. Potrzebny jest sposób prostszy i bardziej naturalny. Wybieramy dowolny liść, na przykład o najmniejszym numerze. Niech będzie to numer k. Szukamy liścia sąsiadującego z liściem o numerze l. W tym celu dla każdego liścia m wyznaczamy długość wspólnego odcinka dróg z k do l i z k do m. Jeśli te drogi rozchodzą się w węźle p, to
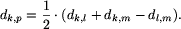
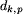 jest największa wtedy, gdy liść m
sąsiaduje z liściem l. W obu przypadkach znajdujemy
parę liści sąsiednich: najczęściej będzie to liść
l i pewien liść m, może się też zdarzyć, że
będą to liście k i l. Poszukiwanie takiej pary
liści sąsiednich wymaga czasu O(n), zatem cały
algorytm działa w czasie O(n2).
jest największa wtedy, gdy liść m
sąsiaduje z liściem l. W obu przypadkach znajdujemy
parę liści sąsiednich: najczęściej będzie to liść
l i pewien liść m, może się też zdarzyć, że
będą to liście k i l. Poszukiwanie takiej pary
liści sąsiednich wymaga czasu O(n), zatem cały
algorytm działa w czasie O(n2).
Inny algorytm polega na sukcesywnym budowaniu drzewa.
Zaczynamy od drzewa złożonego tylko z liści o numerach 1
i 2 i krawędzi łączącej te liście. Ma ona długość
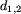 . W naszym przykładzie to drzewo ma postać:
. W naszym przykładzie to drzewo ma postać:
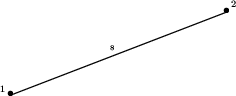
Teraz dołączamy następny liść. Na drodze z liścia 1 do liścia 2 znajduje się węzeł (nadamy mu numer 8), w którym odgałęzia się droga do liścia 3. Można łatwo wyznaczyć długość odcinka od liścia 3 do węzła 8:
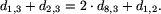
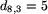 i następnie
i następnie

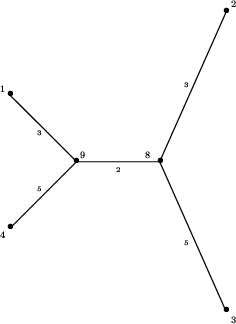
Teraz dołączamy kolejny liść, o numerze 4, wraz z węzłem sąsiadującym z nim. Mamy trzy możliwości. Droga prowadząca z liścia 4 do któregokolwiek z pozostałych liści musi ,,dołączyć'' się do jednej z dróg: z liścia 1 do węzła 8, z liścia 2 do węzła 8 lub z liścia 3 do węzła 8. Oznaczmy liście i węzły literami: węzeł 8 oznaczmy literą m, liść 4 oznaczmy literą l, literą k oznaczmy ten z liści 1,2 lub 3, dla którego droga z k do l nie przechodzi przez m. Pozostałe dwa liście oznaczymy literami i oraz j. Wreszcie literą p oznaczymy węzeł na drodze z k do m, w którym odgałęzia się droga do l. Tę sytuację możemy przedstawić na rysunku:
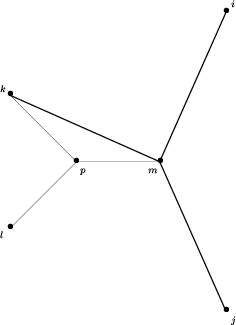
Na rysunku grubszą linią zaznaczono krawędzie drzewa przed dołączeniem liścia l i węzła p, cieńszymi liniami zaznaczono krawędzie drzewa po dołączeniu tych nowych wierzchołków. Zauważmy, że musi być spełniona nierówność
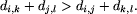
Teraz musimy dołączyć do drzewa następny liść, o
numerze 5. Możliwe są dwa przypadki: droga od liścia 5
do zbudowanego dotychczas drzewa może ,,dołączyć się''
do krawędzi łączącej liść z sąsiednim węzłem lub
do krawędzi łączącej dwa węzły. Można łatwo
stwierdzić, czy ta droga dołączyła się do krawędzi
wychodzącej z liścia.
Przypuśćmy, że mamy dane drzewo i dołączamy nowy
liść l. Załóżmy, że droga z liścia l do drzewa
dołącza się do krawędzi łączącej liść k z
sąsiednim węzłem m. Oznaczmy literą n węzeł, w
którym ta droga dołącza się do krawędzi łączącej
k z m. Niech wreszcie i i j będą dwoma dowolnymi
liśćmi naszego drzewa, różnymi od liścia k. Na
następnych dwóch rysunkach widzimy możliwe położenia
tych liści i węzłów (grubą linią są zaznaczone
krawędzie drzewa, cienką linią drogi w drzewie i nowe
krawędzie po dołączeniu liścia l i węzła n).
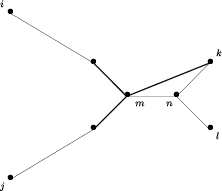
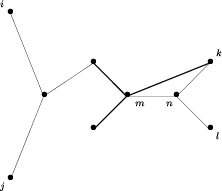
Sytuacja ta jest możliwa tylko wtedy, gdy zachodzi nierówność
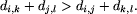
Można postąpić dwojako. Przypuśćmy, że mamy dołączyć nowy liść l w węźle n znajdującym się na krawędzi łączącej dwa węzły m i k. Niech i i j będą dwoma pozostałymi sąsiadami węzła m. Możemy obliczyć odległości od liścia l do wierzchołków i, j i k (ćwiczeniem dla Czytelnika będzie, jak to zrobić). Dalej postępujemy tak samo: musi być spełniona nierówność
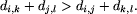
Oczywiście długości krawędzi obliczamy korzystając z
tych samych wzorów co poprzednio.
W ten sposób dołączamy kolejne liście i po dołączeniu
ostatniego drzewo zostało zrekonstruowane. Czas działania
tego algorytmu jest również rzędu O(n2).
W naszym przykładzie kolejne liście zostaną dołączone do krawędzi łączących inne liście z sąsiednimi węzłami. Na dalszych rysunkach widzimy kolejne drzewa powstające przez dołączenie następnych liści.
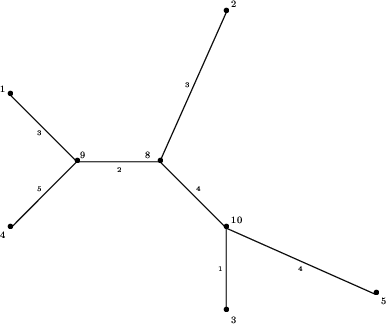
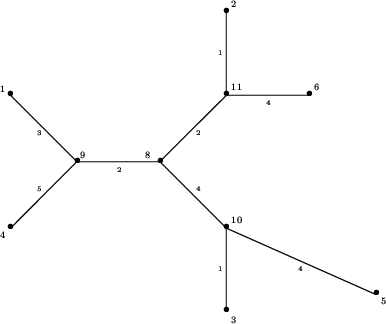
I wreszcie drzewo, o które chodziło:
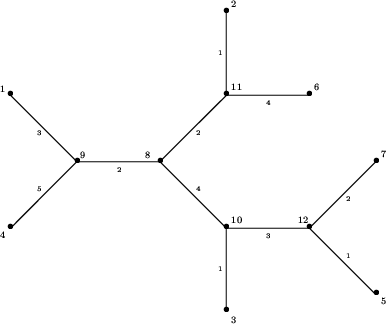
Zadanie to ma zastosowanie w genetyce do wyznaczania tzw. drzew filogenetycznych. Są to drzewa, których liśćmi są gatunki zwierząt lub roślin, a odległości wskazują, jak bardzo dane gatunki są odległe od siebie ewolucyjnie. Rekonstrukcja drzewa sugeruje możliwe kierunki ewolucji: wskazuje, które gatunki mogły powstać bezpośrednio z innych (są to gatunki połączone krawędzią).
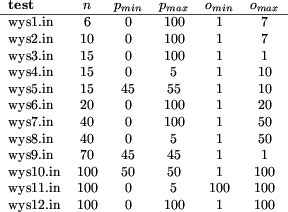
Testy zostały stworzone automatycznie, charakteryzuje je 5 wartości, przy tworzeniu drzewa binarnego:
Jeśli procent liści jest bliski 50, to otrzymamy drzewo pełne. Jeśli bliski 0, będzie to lista. Jeśli będzie dowolny od 0 do 100 to otrzymamy drzewo losowe, czyli zrównoważone.